KL散度在各领域不同的使用情况

相对熵，又称为KL散度（Kullback-Leibler divergence），是两个概率分布P和Q差别的非对称性的度量。近日，CMU的助理教授Simon DeDeo就在推特上表示：“用到KL散度的领域十分广泛，包括心理学、认知学（epistemic）、热力学、统计学、计算、几何学等等。关于这个话题我能开一场研讨会。”

于是，Simon Dedeo就在他的推特上列出了KL散度在各领域不同的使用情况，并附上相关文章。论智整理编译如下：

心理学

在心理学领域，KL散度可以作为预测注意力指向哪里的优秀预测器。在美国南加州大学2005年发表的一篇论文中，研究人员用数据流和新颖的数学方法探究了人们在惊讶情况下大脑的反应。他们认为，惊讶是一种一般的、理论上的概念，它可以由第一原理生成，并还可以通过时空尺寸、感觉形态和数据类型及数据来源形成。

利用贝叶斯框架理论，研究人员捕捉到实验对象的先验概率分布，然后将背景信息表示为：

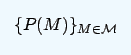
其中模型或假设为M。有了先验分布，新数据带来的基本影响D将先验分布转换为后验分布{P(M|D)}，表示为：

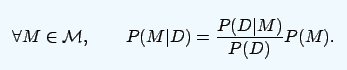
在这个框架中，如果实验对象的情绪未受影响，那么D就不含有惊讶情绪，即后验和先验是一样的。反之，如果研究对象产生惊讶的情绪，那么后验和先验就会产生距离。于是研究人员通过测量后验和先验之间的距离，间接地测出是否有惊讶知情。这就用到了KL散度，表示为：

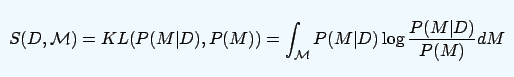
论文地址：ilab.usc.edu/surprise/

认知学

KL散度可以作为决定实验方向的测量标准（让模型产生的效果最大化）。通常，T-optimality是用来获得最优设计，以分辨具有正态分布的同方差模型。该功能经过拓展，还用于研究文学中异方差情况和二元响应模型。在2007年的一篇论文中，来自西班牙和意大利的研究人员提出了一种基于KL距离的新标准，用于区分相应的不具有动态分布的模型。

统计学

KL散度在统计学中的应用可就太多了，但是作者重点讨论了它作为测量近似求解法失败的工具。 在作者曾经写的博客中有这样一个例子：假设我们是太空科学家，到了一座遥远的陌生星球，我们想研究星球上一种虫子，这种虫子有10颗牙齿，但是长期生活过后，虫子的牙齿会脱落一部分，收集了一部分样本后，我们得到了以下牙齿数量分布：

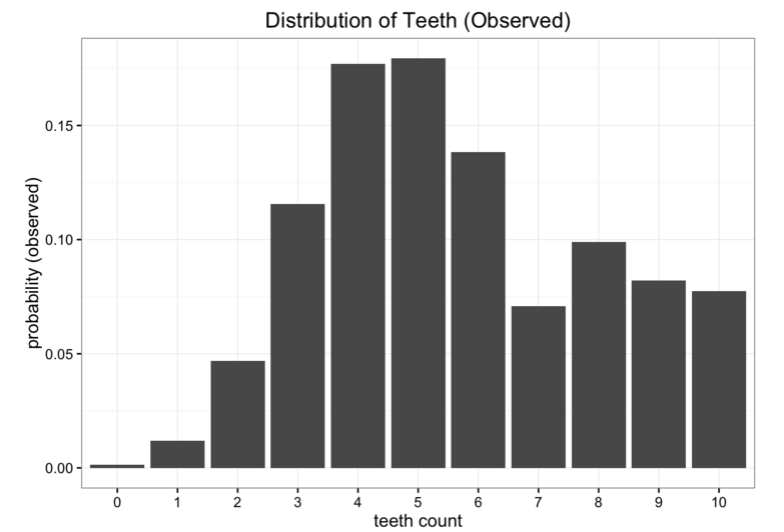
虽然数据很好，但是有一点问题。我们离地球太远了，传输数据回去的成本太高。我们现在想将数据简化成简单模型，只保留一两个参数。其中一种方法是用一种均匀分布的方式表示虫子的牙齿数量。我们知道一共存在11种可能的情况：

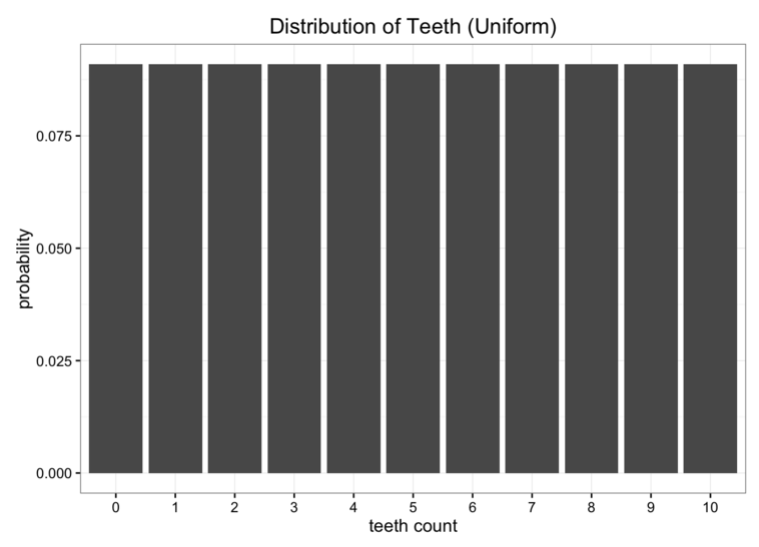
很显然，我们的数据并不是均匀分布的，但是它看起来也不像我们通常所见的某种分布形态。另一种方法是我们可以试着用二项分布对数据建模。在这个案例中，我们需要做的就是估计二项分布中概率参数。我们知道，假设试验次数为n，概率为p，那么期望值就是E[x]=n⋅p。在这个案例中，n=10，期望值就是我们数据的平均数，假设是5.7吧。所以我们对p的最佳估计就是0.57.得到的二项分布如下：

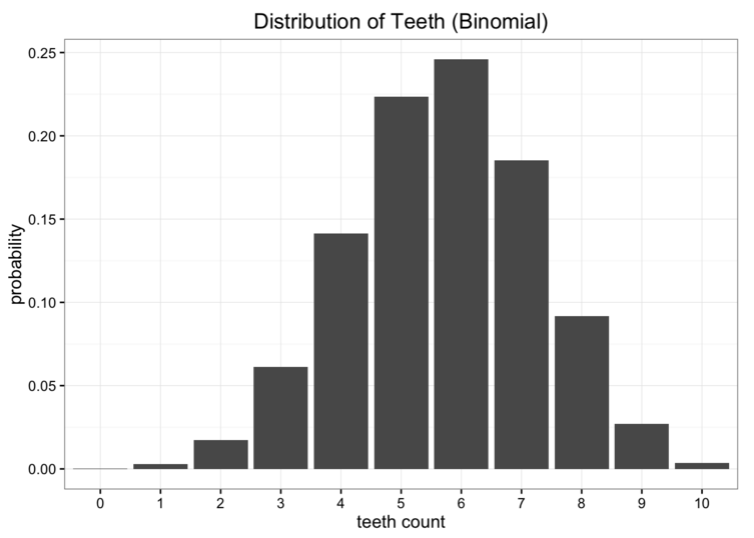
将这些模型与原始数据对比，没有一个能完美契合的，但是哪个更好呢？

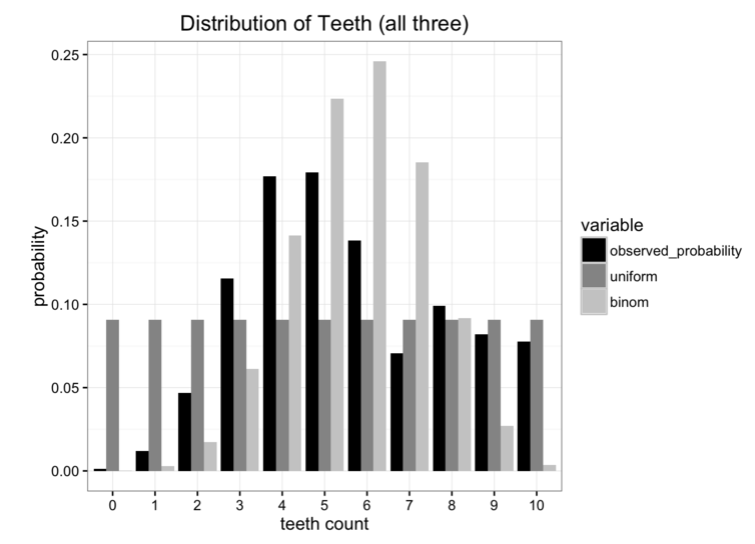
其中虽然存在一些错误的指标，但我们最初的目的是尽量减少发送的信息。所以，想要知道那种模型保留了原始数据最多的信息，最好的方法就是用KL散度。

计算（机器学习）

KL散度可以作为检测模型是否有效的工具，即可以显示模型留有多少的无用信息。在Still等人2012年发表的一篇论文中，他们为了测试模型的质量，利用KL散度。

另一个机器学习的应用：将KL散度（通常在这种情况下被称为“交叉熵”）当做自动编码器、深度学习等的基本损失函数。

另外，还可用作算法公平性（algorithmic fairness）。如何以最佳方式限制一个预测算法，同时还要保证公平。本文作者与2016年发表论文，研究了大数据中的变量问题。

作者认为，当我们用机器学习处理公共政策时，我们发现很多有用的变量与其他一些有问题的变量结合在了一起。这一现象在大数据时代更加严重，有些预测根本没有强有力的理论支撑。如果高质量算法无法提供有力的证明，那么随意做出决策是非常危险的。为了保证预测的准确性，作者用KL散度对两种决策进行比较。

论文地址：arxiv.org/abs/1412.4643

计算（压缩）

当为一种系统设计的压缩算法无法应用到另一种系统上时，就需要用KL散度进行计算。

文化发展

我们认为KL散度还可以作为研究个人发展与创新人物的测量标准。在2016年的一篇论文中，研究人员认为，在一个不确定资源分布的陌生环境中进行研究，总会在新旧发现中摇摆不定，二者要进行权衡。在查找信息的过程中也是如此，求知若渴的人总会犹豫，是在已知领域深究，还是开发新领域的研究呢？为了研究这一决策过程，他们以达尔文为例，找出了他的阅读笔记中出现的所有书，并用KL散度生成了一个模型，量化了他的读书选择。

论文地址：www.sciencedirect.com/science/article/pii/S0010027716302840

同时，KL散度还能用来研究竞争与合作的创造以及想法的分享。在前不久发表的论文中，美国研究人员就利用KL散度研究在法国大革命期间，人们是如何做出民主决策的。

论文地址：www.pnas.org/content/115/18/4607.short

量子理论

剑桥大学的学生Felix Leditzky写了一本关于相对熵的介绍及其在量子理论中的应用的博士论文，其中包括KL散度是如何在互换算子的情况下生成量子的。论文共200页，感兴趣的同学可以拜读一下。

论文地址：pdfs.semanticscholar.org/30a7/6a44a4f0f882c58bd0b636d6393956258c3f.pdf

用户@postquantum补充：“如果你有一些受限的操作类别，那么KL散度会告诉你你需要多少原材料（研究成果、量子纠缠、信息），这种测量是独一无二的。”具体可参考论文：arxiv.org/abs/quant-ph/0207177

另外如果你想使用广义熵和超统计学（即耦合系统），这是Rényi熵的特殊情况。

论文地址：www.pnas.org/content/108/16/6390

数字人文学科

KL散度与TFIDF相关，但是当它涉及粗粒化时，KL散度的性能更好。（特征最明显的单词在梳理文件时部分KL较高；停止词的KL值最低）。具体可查看相关论文。

论文地址：www.mdpi.com/1099-4300/15/6/2246

经济学

另外，KL散度在经济学中也有出现，推特用户@itsaguytalking就发表论文，用KL散度研究不同国家之间的贸易情况，论文研究的目的是如何测量不同意见之间的距离。

论文地址：www.columbia.edu/~ez2197/HowToMeasureDisagreement.pdf

生物学

在2015年的一篇论文中，研究者Nihat Ay认为，随机交互单元的相互依赖型通常由静态联合概率分布的KL散度量化得来的，而概率分布来自对应的参数集合上。本文中的设置由静态扩展为动态版本，利用马尔科夫链信息几何来捕捉暂时的相互依赖关系。

论文地址：www.mdpi.com/1099-4300/17/4/2432

几何学

将微分几何扩展到概率单纯形时，KL散度作为非测量连接。

热力学

一项可以从不平衡的系统中提取的测量方法，使其达到平衡。

结语

由此可见，KL散度作为概率的概念之一，在多个领域都得到了应用。除了上述所介绍的领域外，KL散度最常用的领域还是统计学。除了上文所说的用处，在模型选择上，它还是赤池信息量准则的基础标准。