深入浅出地介绍集成、Bagging、随机森林、特征重要性

现在，假设你已经为某一特定问题选中了最佳的模型，并在进一步提升其精确度上遇到了困难。在这一情形下，你将需要应用一些更高级的机器学习技术——集成（ensemble）。

集成是一组协作贡献的元素。一个熟悉的例子是合奏，组合不同的乐器创建动听的和声。在集成中，最终的整体输出比任何单个部分的表现更重要。

1. 集成

某种意义上，孔多塞陪审团定理描述了我们之前提到的集成。该定理的内容为，如果评审团的每个成员做出独立判断，并且每个陪审员做出正确决策的概率高于0.5，那么整个评审团做出正确的总体决策的概率随着陪审员数量的增加而增加，并趋向于一。另一方面，如果每个陪审员判断正确的概率小于0.5，那么整个陪审团做出正确的总体决策的概率随着陪审员数量的增加而减少，并趋向于零。

该定理形式化的表述为：

N为陪审员总数；

m是构成多数的最小值，即m= (N+1)/2；

p为评审员做出正确决策的概率；

μ是整个评审团做出正确决策的概率。

则：

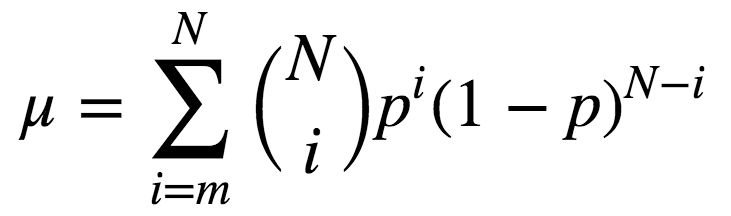
由上式可知，若p > 0.5，则μ > p。此外，若N -> ∞，则μ -> 1。

让我们看另一个集成的例子：群体的智慧。1906年，Francis Galton访问了普利茅斯的一个农村集市，在那里他看到一项竞赛。800个参与者尝试估计一头屠宰的牛的重量。真实重量为1198磅。尽管没人猜中这一数值，所有参与者的预测的平均值为1197磅。

机器学习领域采用类似的思路以降低误差。

2. Bootstraping

Leo Breiman于1994年提出的Bagging（又称Bootstrap aggregation，引导聚集）是最基本的集成技术之一。Bagging基于统计学中的bootstraping（自助法），该方法使得评估许多复杂模型的统计数据更可行。

bootstrap方法的流程如下：假设有尺寸为N的样本X。我们可以从该样本中有放回地随机均匀抽取N个样本，以创建一个新样本。换句话说，我们从尺寸为N的原样本中随机选择一个元素，并重复此过程N次。选中所有元素的可能性是一样的，因此每个元素被抽中的概率均为1/N。

假设我们从一个袋子中抽球，每次抽一个。在每一步中，将选中的球放回袋子，这样下一次抽取是等概率的，即，从同样数量的N个球中抽取。注意，因为我们把球放回了，新样本中可能有重复的球。让我们把这个新样本称为X1。

重复这一过程M次，我们创建M个bootstrap样本X1，……，XM。最后，我们有了足够数量的样本，可以计算原始分布的多种统计数据。

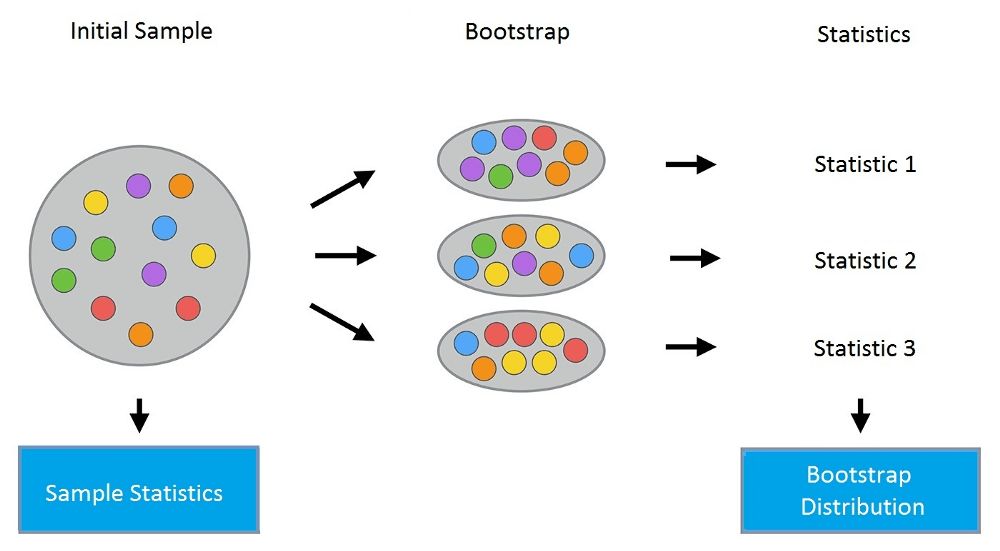
让我们看一个例子，我们将使用之前的telecom_churn数据集。我们曾经讨论过这一数据集的特征重要性，其中最重要的特征之一是呼叫客服次数。让我们可视化这一数据，看看该特征的分布。

import pandas as pd

from matplotlib import pyplot as plt

plt.style.use('ggplot')

plt.rcParams['figure.figsize'] = 10, 6

import seaborn as sns

%matplotlib inline

telecom_data = pd.read_csv('../../data/telecom_churn.csv')

fig = sns.kdeplot(telecom_data[telecom_data['Churn'] == False]['Customer service calls'],

label = 'Loyal')

fig = sns.kdeplot(telecom_data[telecom_data['Churn'] == True]['Customer service calls'],

label = 'Churn')

fig.set(xlabel='Number of calls', ylabel='Density')

plt.show()

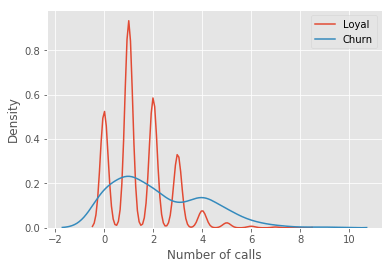
如你所见，相比那些逐渐离网的客户，忠实客户呼叫客服的次数更少。估计每组客户的平均呼叫客服数可能是个好主意。由于我们的数据集很小，如果直接计算原样本的均值，我们得到的估计可能不好。因此我们将应用bootstrap方法。让我们基于原样本生成1000新bootstrap样本，然后计算均值的区间估计。

import numpy as np

def get_bootstrap_samples(data, n_samples):

"""使用bootstrap方法生成bootstrap样本。"""

indices = np.random.randint(0, len(data), (n_samples, len(data)))

samples = data[indices]

return samples

def stat_intervals(stat, alpha):

"""生成区间估计。"""

boundaries = np.percentile(stat, [100 * alpha / 2., 100 * (1 - alpha / 2.)])

return boundaries

分割数据集，分组为忠实客户和离网客户：

loyal_calls = telecom_data[telecom_data['Churn']

== False]['Customer service calls'].values

churn_calls= telecom_data[telecom_data['Churn']

== True]['Customer service calls'].values

固定随机数种子，以得到可重现的结果。

np.random.seed(0)

使用bootstrap生成样本，计算各自的均值。

loyal_mean_scores = [np.mean(sample)

for sample in get_bootstrap_samples(loyal_calls, 1000)]

churn_mean_scores = [np.mean(sample)

for sample in get_bootstrap_samples(churn_calls, 1000)]

打印区间估计值。

print("忠实客户呼叫客服数: 均值区间",

stat_intervals(loyal_mean_scores, 0.05))

print("离网客户呼叫客服数：均值区间",

stat_intervals(churn_mean_scores, 0.05))

结果：

忠实客户呼叫客服数: 均值区间 [1.40771931.49473684]

离网客户呼叫客服数：均值区间 [2.06211182.39761905]

因此，我们看到，有95%的概率，忠实客户平均呼叫客服的次数在1.4到1.49之间，而离网客户平均呼叫客服的次数在2.06到2.40之间。另外，注意忠实客户的区间更窄，这是合理的，因为，相比多次呼叫客服，最终受够了转换运营商的离网客户，忠实客户呼叫客服的次数更少（0、1、2）。

3. Bagging

理解了bootstrap概念之后，我们来介绍bagging。

假设我们有一个训练集X。我们使用bootstrap生成样本X1, ..., XM。现在，我们在每个bootstrap样本上分别训练分类器ai(x)。最终分类器将对所有这些单独的分类器的输出取均值。在分类情形下，该技术对应投票（voting）：

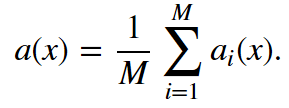
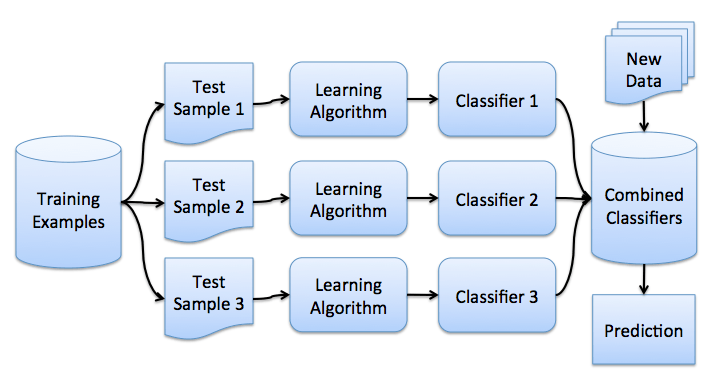
在回归问题中，通过对回归结果取均值，bagging将均方误差降至1/M（M为回归器数量）。

回顾一下上一课的内容，模型的预测误差有三部分构成：

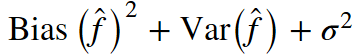
bagging通过在不同数据集上训练模型降低分类器的方差。换句话说，bagging可以预防过拟合。bagging的有效性来自不同训练数据集上单独模型的不同，它们的误差在投票过程中相互抵消。此外，某些bootstrap训练样本很可能略去离散值。

让我们看下bagging的实际效果，并与决策树比较下。我们将使用sklearn文档中的一个例子。

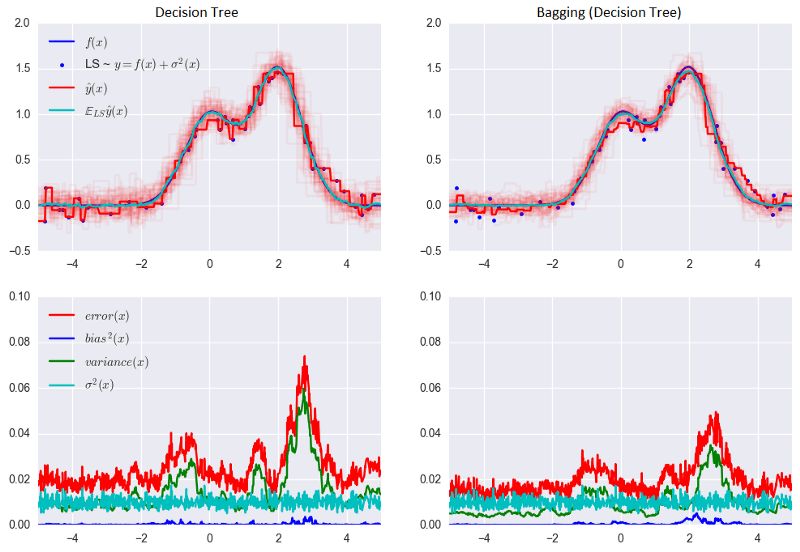
从上图可以看到，就bagging而言，误差中的方差显著降低了。

上面的例子不太可能在实际工作中出现。因为我们做了一个很强的假定，单独误差是不相关的。对现实世界的应用而言，这经常是过于乐观了。当这个假定为假时，误差的下降不会那么显著。在后续课程中，我们将讨论一些更复杂的集成方法，能够在现实世界的问题中做出更精确的预测。

4. 袋外误差

随机森林不需要使用交叉验证或留置样本，因为在这一集成技术内置了误差估计。

随机森林中的决策树基于原始数据集中不同的bootstrap样本构建。对第K棵树而言，其特定bootstrap样本大约留置了37%的输入。

这很容易证明。设数据集中有l个样本。在每一步，每个数据点最终出现在有放回的bootstrap样本中的概率均为1/l。bootstrap样本最终不包含特定数据集元素的概率（即，该元素在l次抽取中都没抽中）等于(1 - 1/l)l。当l -> +∞时，这一概率等于1/e。因此，选中某一特定样本的概率为1 - 1/e，约等于63%。

下面让我们可视化袋外误差（Out-of-BagError，OOBE）估计是如何工作的：

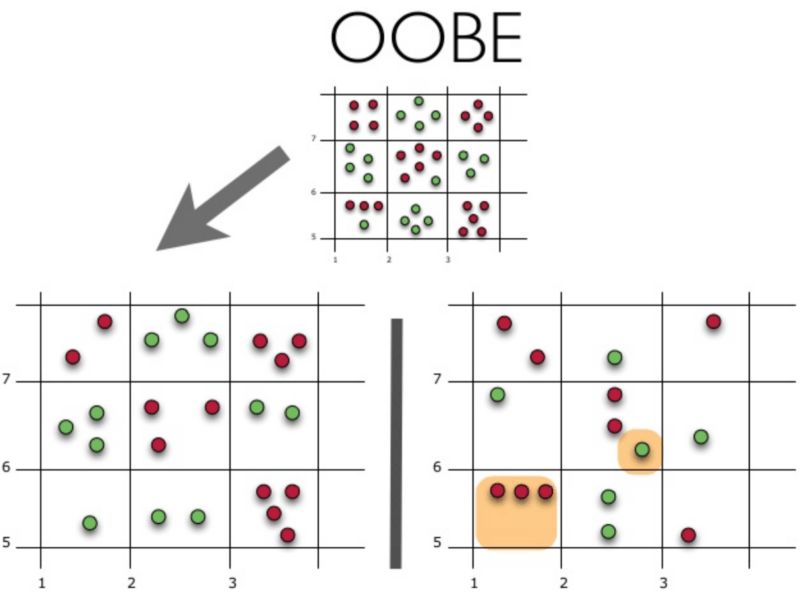
示意图上方为原始数据集。我们将其分为训练集（左）和测试集（右）。在测试集上，我们绘制一副网格，完美地实施了分类。现在，我们应用同一副网格于测试集，以估计分类的正确率。我们可以看到，分类器在4个未曾在训练中使用的数据点上给出了错误的答案。而测试集中共有15个数据点，这15个数据点未在训练中使用。因此，我们的分类器的精确度为11/15 * 100% = 73.33%.

总结一下，每个基础算法在约63%的原始样本上训练。该算法可以在剩下的约37%的样本上验证。袋外估计不过是基础算法在训练过程中留置出来的约37%的输入上的平均估计。

5. 随机森林

Leo Breiman不仅将bootstrap应用于统计，同时也将其应用于机器学习。他和Adel Cutler扩展并改进了Tin Kam Ho提出的的随机森林算法。他们组合使用CART、bagging、随机子空间方法构建无关树。

在bagging中，决策树是一个基础分类器的好选项，因为它们相当复杂，并能在任何样本上达到零分类误差。随机子空间方法降低树的相关性，从而避免过拟合。基于bagging，基础算法在不同的原始特征集的随机子集上训练。

以下算法使用随机子空间方法构建模型集成：

设样本数等于n，特征维度数等于d。

选择集成中单个模型的数目M。

对于每个模型m，选择特征数dm < d。所有模型使用相同的dm值。

对每个模型m，通过在整个d特征集合上随机选择dm个特征创建一个训练集。

训练每个模型。

通过组合M中的所有模型的结果，应用所得集成模型于新输入。可以使用大多数投票（majority voting）或后验概率加总（aggregation of the posterior probabilities）。

5.1 算法

构建N树随机森林的算法如下：

对每个k = 1, ..., N：

生成bootstrap样本Xk。

在样本Xk上创建一棵决策树bk：

根据给定的标准选择最佳的特征维度。根据该特征分割样本以创建树的新层次。重复这一流程，直到竭尽样本。

创建树，直到任何叶节点包含不超过nmin个实例，或者达到特定深度。

对每个分割，我们首先从d个原始特征中随机选择m个特征，接着只在该子集上搜索最佳分割。

最终分类器定义为：

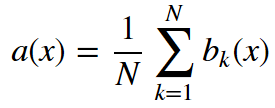
分类问题使用多数投票，回归问题使用均值。

在分类问题中，建议将m设定为d的平方根，取nmin= 1。回归问题中，一般取m = d/3，nmin= 5。

你可以将随机森林看成决策树bagging加上一个改动，在每个分割处选择一个随机特征子空间。

5.2 与决策树和bagging的比较

导入所需包，配置环境：

import warnings

import numpy as np

warnings.filterwarnings('ignore')

%matplotlib inline

from matplotlib import pyplot as plt

plt.style.use('ggplot')

plt.rcParams['figure.figsize'] = 10, 6

import seaborn as sns

from sklearn.ensemble importRandomForestRegressor, RandomForestClassifier

from sklearn.ensemble importBaggingClassifier, BaggingRegressor

from sklearn.tree importDecisionTreeRegressor, DecisionTreeClassifier

from sklearn.datasets import make_circles

from sklearn.model_selection import train_test_split

n_train = 150

n_test = 1000

noise = 0.1

生成数据：

def f(x):

x = x.ravel()

return np.exp(-x ** 2) + 1.5 * np.exp(-(x - 2) ** 2)

def generate(n_samples, noise):

X = np.random.rand(n_samples) * 10 - 5

X = np.sort(X).ravel()

y = np.exp(-X ** 2) + 1.5 * np.exp(-(X - 2) ** 2)\

+ np.random.normal(0.0, noise, n_samples)

X = X.reshape((n_samples, 1))

return X, y

X_train, y_train = generate(n_samples=n_train, noise=noise)

X_test, y_test = generate(n_samples=n_test, noise=noise)

单棵决策树回归：

dtree = DecisionTreeRegressor().fit(X_train, y_train)

d_predict = dtree.predict(X_test)

plt.figure(figsize=(10, 6))

plt.plot(X_test, f(X_test), "b")

plt.scatter(X_train, y_train, c="b", s=20)

plt.plot(X_test, d_predict, "g", lw=2)

plt.xlim([-5, 5])

plt.title("Decision tree, MSE = %.2f"

% np.sum((y_test - d_predict) ** 2))

决策树回归bagging：

bdt = BaggingRegressor(DecisionTreeRegressor()).fit(X_train, y_train)

bdt_predict = bdt.predict(X_test)

plt.figure(figsize=(10, 6))

plt.plot(X_test, f(X_test), "b")

plt.scatter(X_train, y_train, c="b", s=20)

plt.plot(X_test, bdt_predict, "y", lw=2)

plt.xlim([-5, 5])

plt.title("Bagging for decision trees, MSE = %.2f" % np.sum((y_test - bdt_predict) ** 2));

随机森林：

rf = RandomForestRegressor(n_estimators=10).fit(X_train, y_train)

rf_predict = rf.predict(X_test)

plt.figure(figsize=(10, 6))

plt.plot(X_test, f(X_test), "b")

plt.scatter(X_train, y_train, c="b", s=20)

plt.plot(X_test, rf_predict, "r", lw=2)

plt.xlim([-5, 5])

plt.title("Random forest, MSE = %.2f" % np.sum((y_test - rf_predict) ** 2));

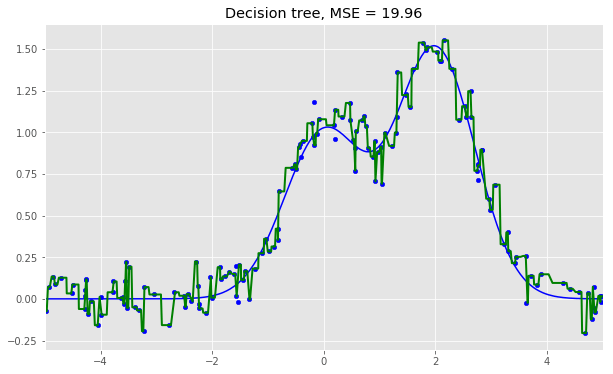
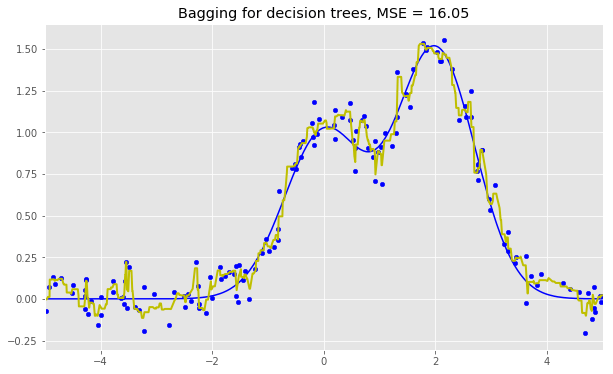
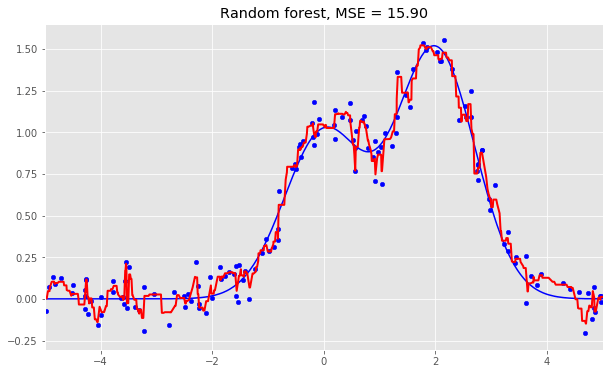
从上面的图像和MSE值可以看到，10树随机森林比单棵决策树和10树bagging的表现要好。（译者注：实际上，在这个例子中，随机森林的表现并不稳定，多次运行的结果是，随机森林和bagging互有胜负。）随机森林和bagging的主要差别在于，在随机森林中，分割的最佳特征是从一个随机特征子空间中选取的，而在bagging中，分割时将考虑所有特征。

接下来，我们将查看随机森林和bagging在分类问题上的表现：

np.random.seed(42)

X, y = make_circles(n_samples=500, factor=0.1, noise=0.35, random_state=42)

X_train_circles, X_test_circles, y_train_circles, y_test_circles = train_test_split(X, y, test_size=0.2)

dtree = DecisionTreeClassifier(random_state=42)

dtree.fit(X_train_circles, y_train_circles)

x_range = np.linspace(X.min(), X.max(), 100)

xx1, xx2 = np.meshgrid(x_range, x_range)

y_hat = dtree.predict(np.c_[xx1.ravel(), xx2.ravel()])

y_hat = y_hat.reshape(xx1.shape)

plt.contourf(xx1, xx2, y_hat, alpha=0.2)

plt.scatter(X[:,0], X[:,1], c=y, cmap='autumn')

plt.title("Decision tree")

plt.show()

b_dtree = BaggingClassifier(DecisionTreeClassifier(),n_estimators=300, random_state=42)

b_dtree.fit(X_train_circles, y_train_circles)

x_range = np.linspace(X.min(), X.max(), 100)

xx1, xx2 = np.meshgrid(x_range, x_range)

y_hat = b_dtree.predict(np.c_[xx1.ravel(), xx2.ravel()])

y_hat = y_hat.reshape(xx1.shape)

plt.contourf(xx1, xx2, y_hat, alpha=0.2)

plt.scatter(X[:,0], X[:,1], c=y, cmap='autumn')

plt.title("Bagging (decision trees)")

plt.show()

rf = RandomForestClassifier(n_estimators=300, random_state=42)

rf.fit(X_train_circles, y_train_circles)

x_range = np.linspace(X.min(), X.max(), 100)

xx1, xx2 = np.meshgrid(x_range, x_range)

y_hat = rf.predict(np.c_[xx1.ravel(), xx2.ravel()])

y_hat = y_hat.reshape(xx1.shape)

plt.contourf(xx1, xx2, y_hat, alpha=0.2)

plt.scatter(X[:,0], X[:,1], c=y, cmap='autumn')

plt.title("Random forest")

plt.show()

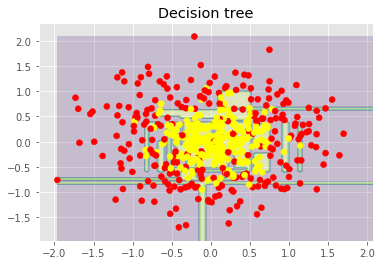
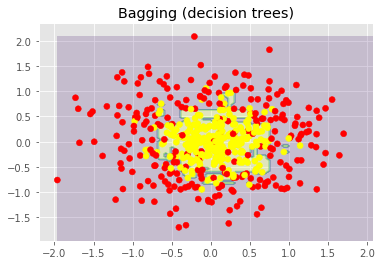
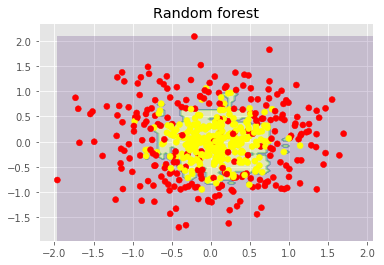
上图显示了决策树判定的边界相当凹凸不平，有大量锐角，这暗示了过拟合，概括性差。相反，随机森林和bagging的边界相当平滑，没有明显的过拟合的迹象。

现在，让我们查看一些有助于提高模型精确度的参数。

5.3 参数

scikit-learn库提供了BaggingRegressor和BaggingClassifier。

下面是创建新模型时需要注意的一些参数：

n_estimators是森林中树的数量；

criterion是衡量分割质量的函数；

max_features是查找最佳分割时考虑的特征数；

min_samples_leaf是叶节点的最小样本数；

max_depth是树的最大深度。

在真实问题中练习随机森林

我们将使用之前的离网预测作为例子。这是一个分类问题，我们将使用精确度评估模型。

import pandas as pd

from sklearn.model_selection import cross_val_score, StratifiedKFold, GridSearchCV

from sklearn.metrics import accuracy_score

df = pd.read_csv("../../data/telecom_churn.csv")

首先，让我们创建一个简单的分类器作为基线。出于简单性，我们将只使用数值特征。

cols = []

for i in df.columns:

if (df[i].dtype == "float64") or (df[i].dtype == 'int64'):

cols.append(i)

分离数据集为输入和目标：

X, y = df[cols].copy(), np.asarray(df["Churn"],dtype='int8')

为验证过程进行分层分割：

skf = StratifiedKFold(n_splits=5, shuffle=True, random_state=42)

基于默认参数初始化分类器：

rfc = RandomForestClassifier(random_state=42, n_jobs=-1, oob_score=True)

在训练集上进行训练：

results = cross_val_score(rfc, X, y, cv=skf)

在测试集上评估精确度：

print("交叉验证精确度评分： {:.2f}%".format(results.mean()*100))

结果：

交叉验证精确度评分：91.48%

现在，让我们尝试改进结果，同时查看下修改基本参数时学习曲线的表现。

让我们从树的数量开始：

skf = StratifiedKFold(n_splits=5, shuffle=True, random_state=42)

创建列表储存训练集和测试集上的精确度数值：

train_acc = []

test_acc = []

temp_train_acc = []

temp_test_acc = []

进行网格搜索：

trees_grid = [5, 10, 15, 20, 30, 50, 75, 100]

在训练集上训练：

for ntrees in trees_grid:

rfc = RandomForestClassifier(n_estimators=ntrees, random_state=42, n_jobs=-1, oob_score=True)

temp_train_acc = []

temp_test_acc = []

for train_index, test_index in skf.split(X, y):

X_train, X_test = X.iloc[train_index], X.iloc[test_index]

y_train, y_test = y[train_index], y[test_index]

rfc.fit(X_train, y_train)

temp_train_acc.append(rfc.score(X_train, y_train))

temp_test_acc.append(rfc.score(X_test, y_test))

train_acc.append(temp_train_acc)

test_acc.append(temp_test_acc)

打印结果：

train_acc, test_acc = np.asarray(train_acc), np.asarray(test_acc)

print("交叉验证最佳精确度为 {:.2f}% 在 {} 树时达到".format(max(test_acc.mean(axis=1))*100,

trees_grid[np.argmax(test_acc.mean(axis=1))]))

结果：

交叉验证最佳精确度为 92.44% 在 50 树时达到

接下来，我们绘制相应的学习曲线：

plt.style.use('ggplot')

fig, ax = plt.subplots(figsize=(8, 4))

ax.plot(trees_grid, train_acc.mean(axis=1), alpha=0.5, color='blue', label='train')

ax.plot(trees_grid, test_acc.mean(axis=1), alpha=0.5, color='red', label='cv')

ax.fill_between(trees_grid, test_acc.mean(axis=1) - test_acc.std(axis=1), test_acc.mean(axis=1) + test_acc.std(axis=1), color='#888888', alpha=0.4)

ax.fill_between(trees_grid, test_acc.mean(axis=1) - 2*test_acc.std(axis=1), test_acc.mean(axis=1) + 2*test_acc.std(axis=1), color='#888888', alpha=0.2)

ax.legend(loc='best')

ax.set_ylim([0.88,1.02])

ax.set_ylabel("Accuracy")

ax.set_xlabel("N_estimators");

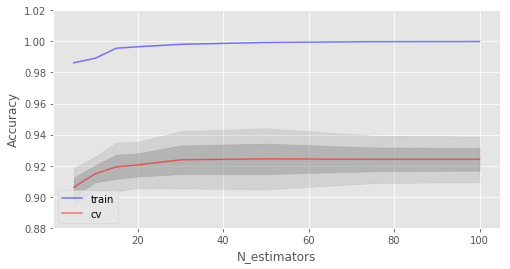
如你所见，当达到特定数量时，测试集上的精确度非常接近渐近线。

上图同时显示了我们在训练集上达到了100%精确度，这意味着我们过拟合了。为了避免过拟合，我们需要给模型加上正则化参数。

下面我们将树的数目固定为100，然后看看不同的max_depth效果如何：

train_acc = []

test_acc = []

temp_train_acc = []

temp_test_acc = []

max_depth_grid = [3, 5, 7, 9, 11, 13, 15, 17, 20, 22, 24]

for max_depth in max_depth_grid:

rfc = RandomForestClassifier(n_estimators=100, random_state=42, n_jobs=-1, oob_score=True, max_depth=max_depth)

temp_train_acc = []

temp_test_acc = []

for train_index, test_index in skf.split(X, y):

X_train, X_test = X.iloc[train_index], X.iloc[test_index]

y_train, y_test = y[train_index], y[test_index]

rfc.fit(X_train, y_train)

temp_train_acc.append(rfc.score(X_train, y_train))

temp_test_acc.append(rfc.score(X_test, y_test))

train_acc.append(temp_train_acc)

test_acc.append(temp_test_acc)

train_acc, test_acc = np.asarray(train_acc), np.asarray(test_acc)

print("交叉验证最佳精确度为 {:.2f}% 当 max_depth 为 {} 时达到".format(max(test_acc.mean(axis=1))*100,

max_depth_grid[np.argmax(test_acc.mean(axis=1))]))

结果：

交叉验证最佳精确度为 92.68% 当 max_depth 为 17 时达到

fig, ax = plt.subplots(figsize=(8, 4))

ax.plot(max_depth_grid, train_acc.mean(axis=1), alpha=0.5, color='blue', label='train')

ax.plot(max_depth_grid, test_acc.mean(axis=1), alpha=0.5, color='red', label='cv')

ax.fill_between(max_depth_grid, test_acc.mean(axis=1) - test_acc.std(axis=1), test_acc.mean(axis=1) + test_acc.std(axis=1), color='#888888', alpha=0.4)

ax.fill_between(max_depth_grid, test_acc.mean(axis=1) - 2*test_acc.std(axis=1), test_acc.mean(axis=1) + 2*test_acc.std(axis=1), color='#888888', alpha=0.2)

ax.legend(loc='best')

ax.set_ylim([0.88,1.02])

ax.set_ylabel("Accuracy")

ax.set_xlabel("Max_depth");

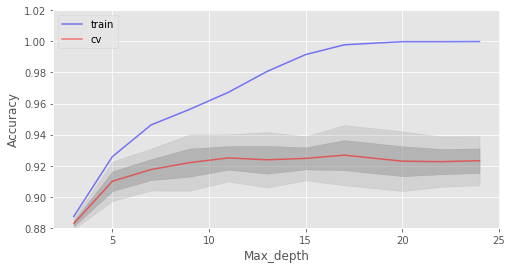
max_depth在我们的模型中起到了正则化的作用，模型不像之前过拟合得那么严重了。模型精确度略有提升。

另一个值得调整的重要参数是min_samples_leaf，它也能起到正则化作用。

train_acc = []

test_acc = []

temp_train_acc = []

temp_test_acc = []

min_samples_leaf_grid = [1, 3, 5, 7, 9, 11, 13, 15, 17, 20, 22, 24]

for min_samples_leaf in min_samples_leaf_grid:

rfc = RandomForestClassifier(n_estimators=100, random_state=42, n_jobs=-1,

oob_score=True, min_samples_leaf=min_samples_leaf)

temp_train_acc = []

temp_test_acc = []

for train_index, test_index in skf.split(X, y):

X_train, X_test = X.iloc[train_index], X.iloc[test_index]

y_train, y_test = y[train_index], y[test_index]

rfc.fit(X_train, y_train)

temp_train_acc.append(rfc.score(X_train, y_train))

temp_test_acc.append(rfc.score(X_test, y_test))

train_acc.append(temp_train_acc)

test_acc.append(temp_test_acc)

train_acc, test_acc = np.asarray(train_acc), np.asarray(test_acc)

print("交叉验证最佳精确度为 {:.2f}% 当 min_samples_leaf 为 {} 时达到".format(max(test_acc.mean(axis=1))*100,

min_samples_leaf_grid[np.argmax(test_acc.mean(axis=1))]))

结果：

交叉验证最佳精确度为 92.41% 当 min_samples_leaf 为 3 时达到

fig, ax = plt.subplots(figsize=(8, 4))

ax.plot(min_samples_leaf_grid, train_acc.mean(axis=1), alpha=0.5, color='blue', label='train')

ax.plot(min_samples_leaf_grid, test_acc.mean(axis=1), alpha=0.5, color='red', label='cv')

ax.fill_between(min_samples_leaf_grid, test_acc.mean(axis=1) - test_acc.std(axis=1), test_acc.mean(axis=1) + test_acc.std(axis=1), color='#888888', alpha=0.4)

ax.fill_between(min_samples_leaf_grid, test_acc.mean(axis=1) - 2*test_acc.std(axis=1), test_acc.mean(axis=1) + 2*test_acc.std(axis=1), color='#888888', alpha=0.2)

ax.legend(loc='best')

ax.set_ylim([0.88,1.02])

ax.set_ylabel("Accuracy")

ax.set_xlabel("Min_samples_leaf");

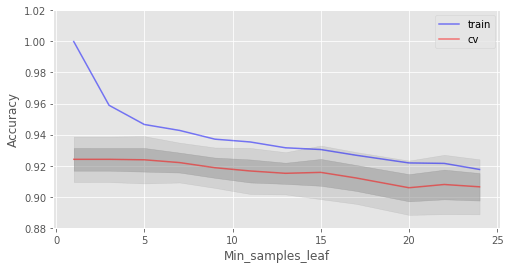
在这一情形下，我们没在验证集上看到精确度提升，但在验证集上精确度保持92%以上的同时，降低了2%的过拟合。

考虑max_features这一参数。在分类问题中，所有特征数的平方根是默认选择。让我们看下4个特征是否是这个例子中的最佳选择：

train_acc = []

test_acc = []

temp_train_acc = []

temp_test_acc = []

max_features_grid = [2, 4, 6, 8, 10, 12, 14, 16]

for max_features in max_features_grid:

rfc = RandomForestClassifier(n_estimators=100, random_state=42, n_jobs=-1,

oob_score=True, max_features=max_features)

temp_train_acc = []

temp_test_acc = []

for train_index, test_index in skf.split(X, y):

X_train, X_test = X.iloc[train_index], X.iloc[test_index]

y_train, y_test = y[train_index], y[test_index]

rfc.fit(X_train, y_train)

temp_train_acc.append(rfc.score(X_train, y_train))

temp_test_acc.append(rfc.score(X_test, y_test))

train_acc.append(temp_train_acc)

test_acc.append(temp_test_acc)

train_acc, test_acc = np.asarray(train_acc), np.asarray(test_acc)

print("交叉验证最佳精确度为 {:.2f}% 当 max_features 为 {} 时达到".format(max(test_acc.mean(axis=1))*100,

max_features_grid[np.argmax(test_acc.mean(axis=1))]))

结果：

交叉验证最佳精确度为 92.59% 当 max_features 为 10 时达到

fig, ax = plt.subplots(figsize=(8, 4))

ax.plot(max_features_grid, train_acc.mean(axis=1), alpha=0.5, color='blue', label='train')

ax.plot(max_features_grid, test_acc.mean(axis=1), alpha=0.5, color='red', label='cv')

ax.fill_between(max_features_grid, test_acc.mean(axis=1) - test_acc.std(axis=1), test_acc.mean(axis=1) + test_acc.std(axis=1), color='#888888', alpha=0.4)

ax.fill_between(max_features_grid, test_acc.mean(axis=1) - 2*test_acc.std(axis=1), test_acc.mean(axis=1) + 2*test_acc.std(axis=1), color='#888888', alpha=0.2)

ax.legend(loc='best')

ax.set_ylim([0.88,1.02])

ax.set_ylabel("Accuracy")

ax.set_xlabel("Max_features");

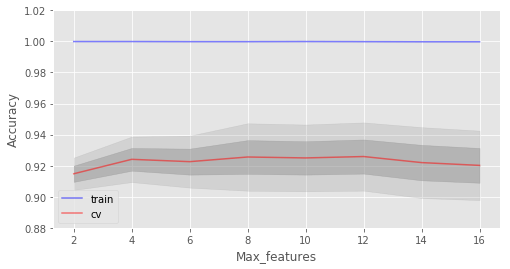
在我们的例子中，最佳特征数是10。

我们已经查看了基本参数的不同值的学习曲线。下面让我们使用GridSearch查找最佳参数：

parameters = {'max_features': [4, 7, 10, 13], 'min_samples_leaf': [1, 3, 5, 7], 'max_depth': [5,10,15,20]}

rfc = RandomForestClassifier(n_estimators=100, random_state=42,

n_jobs=-1, oob_score=True)

gcv = GridSearchCV(rfc, parameters, n_jobs=-1, cv=skf, verbose=1)

gcv.fit(X, y)

gcv.best_estimator_, gcv.best_score_

返回：

(RandomForestClassifier(bootstrap=True, class_weight=None, criterion='gini',

max_depth=10, max_features=10, max_leaf_nodes=None,

min_impurity_decrease=0.0, min_impurity_split=None,

min_samples_leaf=1, min_samples_split=2,

min_weight_fraction_leaf=0.0, n_estimators=100, n_jobs=-1,

oob_score=True, random_state=42, verbose=0, warm_start=False),

0.9270927092709271)

随机森林最重要的一点是它的精确度不会随着树的增加而下降，所以树的数量不像max_depth和min_samples_leaf那样错综复杂。这意味着你可以使用，比如说，10棵树调整超参数，接着增加树的数量至500，放心，精确度只会更好。

5.4 方差和去相关

随机森林的方差可以用下式表达：

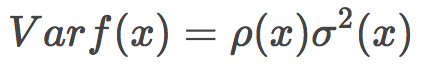
其中

p(x)为任何两棵树之间的样本相关性；

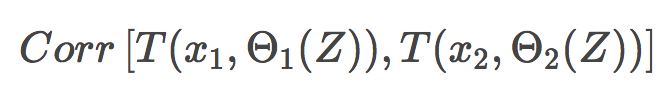
Θ1(Z)和Θ2(Z)为样本Z上随机选择的元素上随机选择的一对树；

T(x, Θi(Z))为第i个树分类器在输入向量x上的输出；

σ2(x)为任何随机选择的树上的样本方差：

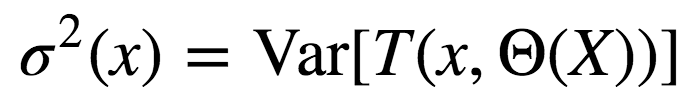
很容易将p(x)误认为给定的随机森林中训练好的树的平均相关性（将树视为N维向量）。其实并非如此。

事实上，这一条件相关性并不和平均过程直接相关，p(x)的自变量x提醒了我们这一差别。p(x)是一对随机树在输入x上的估计的理论相关性。它的值源自重复取样训练集以及之后随机选择的决策树对。用统计学术语来说，这是由Z和Θ取样分布导致的相关性。

任何一对树的条件相关性等于0，因为bootstrap和特征选取是独立同分布。

如果我们考虑单棵树的方差，它几乎不受分割参数的影响（m）。但这一参数在集成中是关键。另外，单棵决策树的方差要比集成高很多。The Elements of Statistical Learning一书中有一个很好的例子：

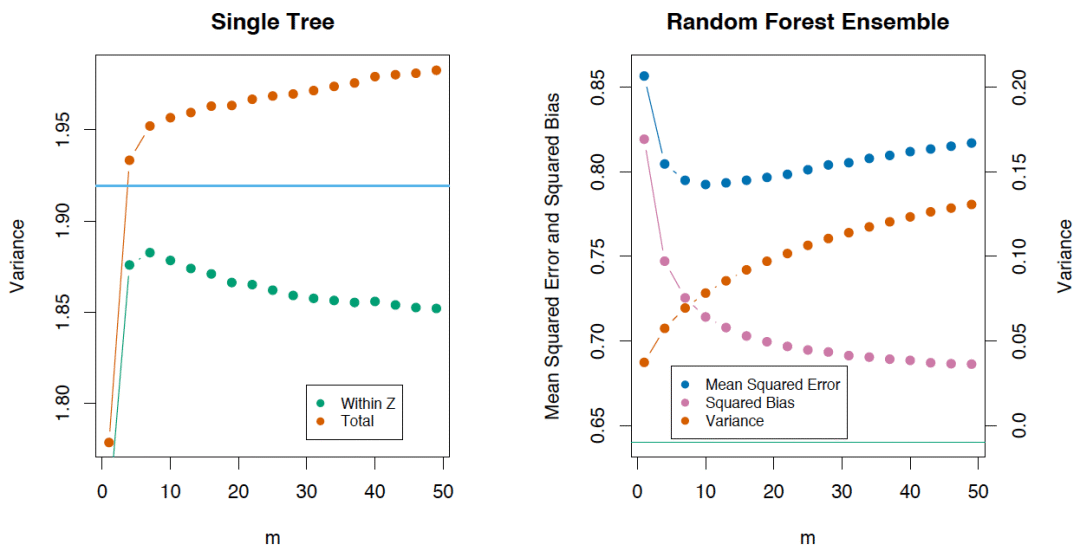
5.5 偏差

随机森林、bagging的偏差和单棵决策树一样：

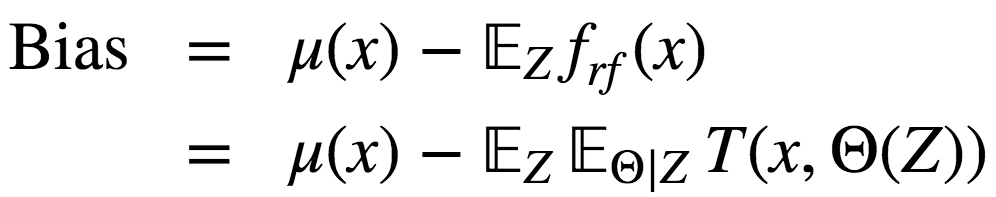
从绝对值上说，偏差通常比单棵树要大，因为随机过程和样本空间缩减在模型上施加了它们各自的限制。因此，bagging和随机森林在预测精确度上的提升单纯源自方差降低。

5.6 极端随机树

极端随机树（Extremely Randomized Trees）在节点分岔时应用了更多随机性。和随机森林一样，极端随机树使用一个随机特征子空间。然而，极端随机数并不搜寻最佳阈值，相反，为每个可能的特征随机生成一个阈值，然后根据其中最佳随机生成阈值对应的特征来分割节点。这通常是用少量偏差的增加交换方差的略微下降。

scikit-learn库实现了[ ExtraTreesClassifier]和ExtraTreesRegressor。

如果你使用随机森林或梯度提升遇到了严重的过拟合，可以试试极端随机树。

5.7 随机森林和k近邻的相似性

随机森林和最近邻技术有相似之处。随机森林预测基于训练集中相似样本的标签。这些样本越常出现在同一叶节点，它们的相似度就越高。下面我们将证明这一点。

让我们考虑一个二次损失函数的回归问题。设Tn(x)为输入x在随机森林中第n棵树的叶节点数。算法对输入向量x的响应等于所有落入叶节点Tn(x)的训练样本的平均响应。

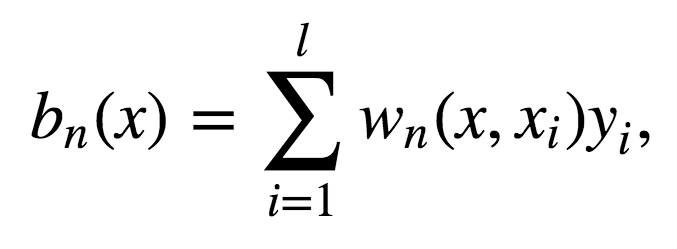
其中

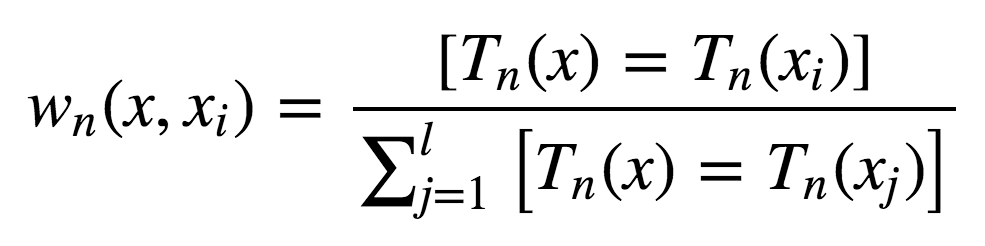
故响应的构成为：

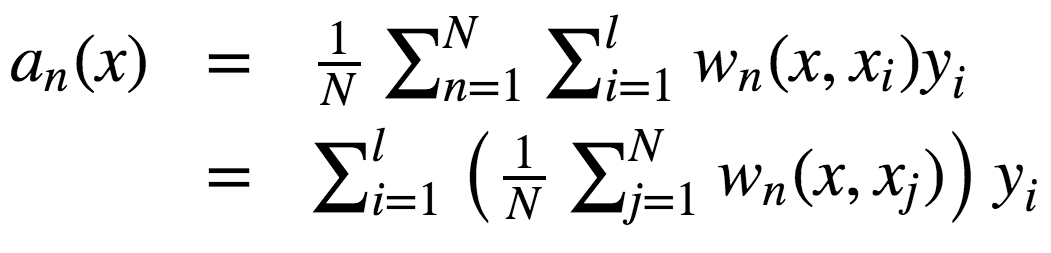
如你所见，随机森林的响应为所有训练样本响应的加权和。

同时，值得注意的是，实例x最终出现的叶节点数Tn(x)，本身是一个有价值的特征。例如，下面的方法效果不错：

基于随机森林或梯度提升技术在样本上训练较小数目的决策树的复合模型

将类别特征T1(x),...,Tn(x)加入样本

这些新特征是非线性空间分割的结果，它们提供了关于样本之间的相似性的信息。The Elements of Statistical Learning一书中有一个很好的说明样例，演示了随机森林和k-近邻技术的相似性：

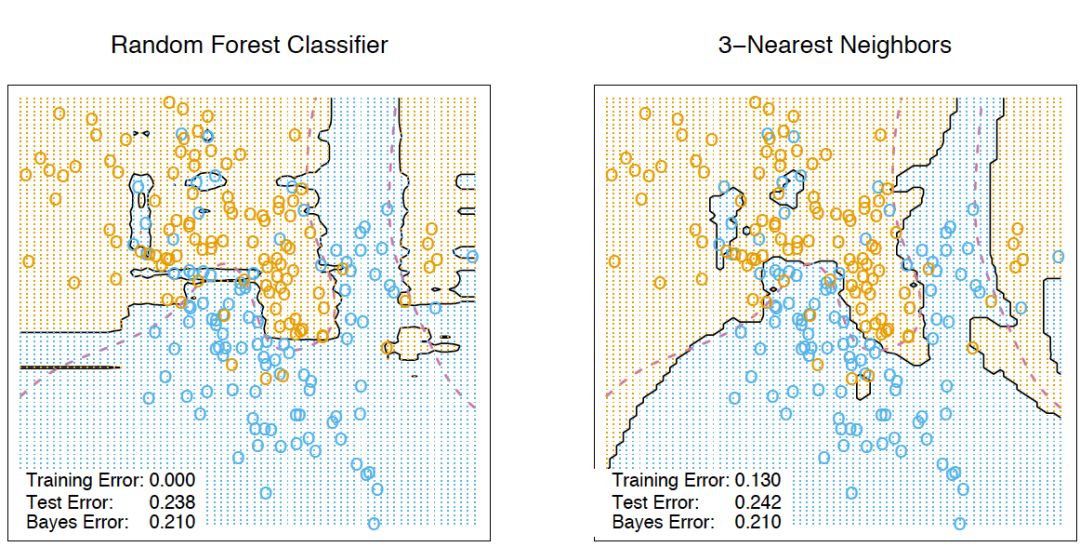
5.8 转换数据集为高维表示

随机森林主要用于监督学习，不过也可以在无监督设定下应用。

使用scikit-learn的RandomTreesEmbedding方法，我们可以将数据集转换为高维的稀疏表示。我们首先创建一些极端随机树，接着使用包含样本的叶节点索引作为新特征。

例如，如果第一个叶节点包含输入，我们分配1为特征值，否则，分配0. 这称为二进制编码（binary coding）。我们可以通过增减树的数目和深度控制特征数量和稀疏性。由于邻居的数据点倾向于落入同一叶节点，这一转换提供了对数据点的密度的一个隐式的非参数估计。

5.9 随机森林的优势和劣势

优势：

高预测精确度；在大多数问题上表现优于线性算法；精确度与boosting相当；

多亏了随机取样，对离散值的鲁棒性较好；

随机子空间选取导致对特征缩放及其他单调转换不敏感；

不需要精细的参数调整，开箱即用。取决于问题设定和数据，调整参数可能取得0.5%到3%的精确度提升；

在具有大量特征和分类的数据集上很高效；

既可处理连续值，也可处理离散值；

罕见过拟合。在实践中，增加树的数量几乎总是能提升总体表现。不过，当达到特定数量后，学习曲线非常接近渐近线；

有成熟方法用于估计特征重要性；

能够很好地处理数据缺失，即使当很大一部分数据缺失时，仍能保持较好的精确度；

支持整个数据集及单棵树样本上的加权分类；

决策树底层使用的实例亲近性计算可以在后续用于聚类、检测离散值、感兴趣数据表示；

以上功能和性质可以扩展到未标注数据，以支持无监督聚类，数据可视化和离散值检测；

易于并行化，伸缩性强。

劣势：

相比单棵决策树，随机森林的输出更难解释。

特征重要性估计没有形式化的p值。

在稀疏数据情形（比如，文本输入、词袋）下，表现不如线性模型好。

和线性回归不同，随机森林无法外推。不过，这也可以看成优势，因为离散值不会在随机森林中导致极端值。

在某些问题上容易过拟合，特别是处理高噪声数据。

处理数量级不同的类别数据时，随机森林偏重数量级较高的变量，因为这能提高更多精确度；

如果数据集包含对预测分类重要度相似的相关特征分组，那么随机森林将偏重较小的分组；

所得模型较大，需要大量RAM。

6. 特征重要性

我们常常需要给出算法输出某个特定答案的原因。或者，在不能完全理解算法的情况下，我们至少想要找出哪个输入特征对结果的贡献最大。基于随机森林，我们可以相当容易地获取这类信息。

方法精要

下图很直观地呈现了，在我们的信用评分问题中，年龄比收入更重要。基于信息增益这一概念，我们可以形式化地解释这一点。

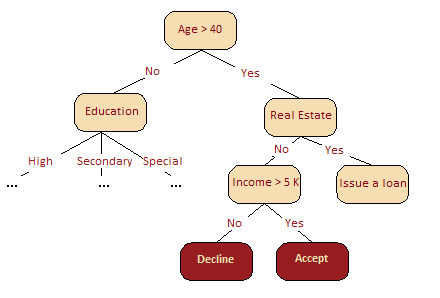
在随机森林中，某一特征在所有树中离树根的平均距离越近，这一特征在给定的分类或回归问题中就越重要。按照分割标准，在每棵树的每处最优分割中取得的增益，例如基尼不纯度（Gini impurity），是与分割特征直接相关的重要度测度。每个特征的评分值不同（通过累加所有树得出）。

让我们深入一些细节。

某个变量导致的平均精确度下降可以通过计算袋外误差判定。由于除外或选定某一变量导致的精确度下降约大，该变量的重要性评分（importance score）就越高。

基尼不纯度——或回归问题中的MSE——的平均下降代表每个变量对所得随机森林模型节点的同质性的贡献程度。每次选中一个变量进行分割时，计算子节点的基尼不纯度，并与原节点进行比较。

基尼不纯度是位于0（同质）到1（异质）之间的同质性评分。为每个变量累加分割标准对应值的变动，并在计算过程的最后加以正则化。基尼不纯度下降较高标志着基于该变量进行的分割可以得到纯度更高的节点。

以上可以用分析形式表达为：

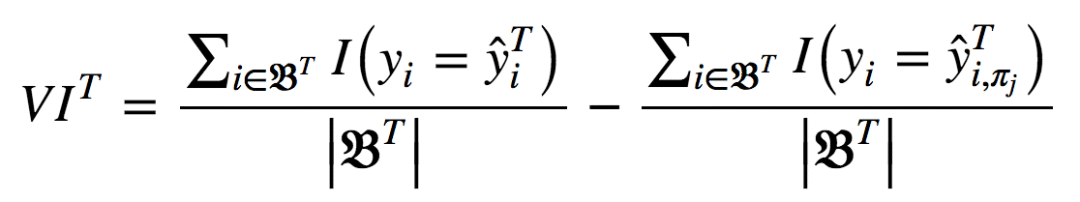
其中，πj表示选中或排除特征。当xj不在树T中时，VIT(xj) = 0。

现在，我们可以给出集成的特征重要性计算公式。

未经正则化：

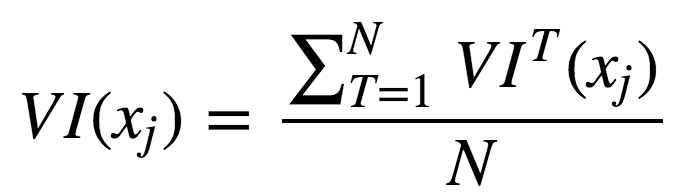
使用标准差正则化后：

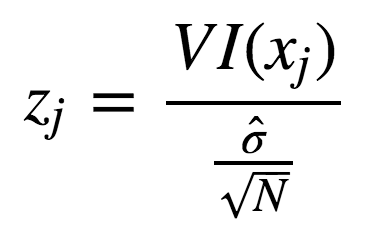
实际操作例子

让我们考虑一项调查结果，关于Booking.com和TripAdvisor.com上列出的旅馆。这里的特征是不同类别（包括服务质量、房间状况、性价比等）的平均评分。目标变量为旅馆在网站上的总评分。

import warnings

warnings.filterwarnings('ignore')

%matplotlib inline

from matplotlib import pyplot as plt

import seaborn as sns

from matplotlib import rc

font = {'family': 'Verdana',

'weight': 'normal'}

rc('font', **font)

import pandas as pd

import numpy as np

from sklearn.ensemble.forest importRandomForestRegressor

hostel_data = pd.read_csv("../../data/hostel_factors.csv")

features = {"f1":u"Staff",

"f2":u"Hostel booking",

"f3":u"Check-in and check-out",

"f4":u"Room condition",

"f5":u"Shared kitchen condition",

"f6":u"Shared space condition",

"f7":u"Extra services",

"f8":u"General conditions & conveniences",

"f9":u"Value for money",

"f10":u"Customer Co-creation"}

forest = RandomForestRegressor(n_estimators=1000, max_features=10,

random_state=0)

forest.fit(hostel_data.drop(['hostel', 'rating'], axis=1),

hostel_data['rating'])

importances = forest.feature_importances_

indices = np.argsort(importances)[::-1]

num_to_plot = 10

feature_indices = [ind+1for ind in indices[:num_to_plot]]

plt.figure(figsize=(15,5))

plt.title(u"Feature Importance")

bars = plt.bar(range(num_to_plot),

importances[indices[:num_to_plot]],

color=([str(i/float(num_to_plot+1))

for i in range(num_to_plot)]),

align="center")

ticks = plt.xticks(range(num_to_plot),

feature_indices)

plt.xlim([-1, num_to_plot])

plt.legend(bars, [u''.join(features["f"+str(i)])

for i in feature_indices]);

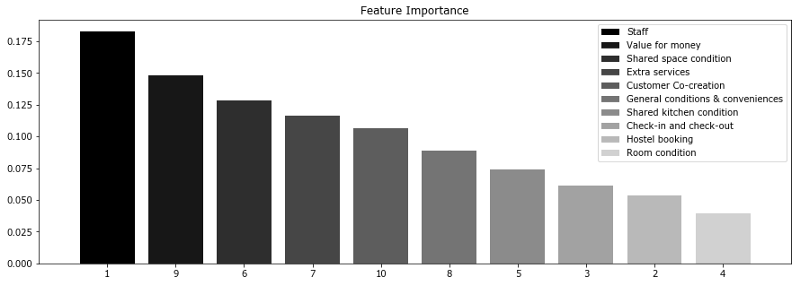
上图显示，消费者常常更为关心服务人员和性价比。这两个因子对最终评分的影响最大。然而，这两项特征和其他特征的差别不是非常大。因此，排除任何特征都会导致模型精确度的下降。基于我们的分析，我们可以建议旅馆业主重点关注服务人员培训和性价比。