0 引言
作为5G通信的关键候选技术之一[1],D2D通信技术可以实现基于邻近服务设备之间的直接通信要求,具有降低服务基站负荷的优势。D2D发现过程作为D2D通信中实现基于邻近服务的第一步,是以设备对之间安装有相同且同处于激活状态的应用程序[2]为前提来实现的。传统上进行D2D发现过程所使用的发现消息是基于应用程序名称设计的,这样不仅使得内存方面不能满足日益增长的数据要求,而且也使得数据传输速率方面有所欠缺。
因此,对此问题的相关文献也不断涌现。文献[3]提出了一种基于hash函数来进行发现消息的构造的方案。文献[4]在文献[3]的基础上添加使用bloom滤波器来进行发现消息的构造,方案中,发现消息基于bloom过滤器数据结构和K个hash函数来设计。由文献[3]、[4]所述,在应用程序发现的过程中,假肯定情况是不可避免的,而且,降低错误的概率则会显著增加发现信息的大小。
由此,本文提出了基于RLE编码二叉树发现消息的设计。发现消息中使用应用程序的标识值范围而不是标识值来减少发现消息的大小,随后通过使用二叉树[5-6]来表示分页的范围,并通过RLE编码[5]的二叉树的比特信息来通知作业设备应用程序的值范围,以此实现高效无误的设备对发现过程。
1 发现过程及其模型
为了方便标识设备中各个应用程序,本文采用应用程序名称对应的ASCII值的总和作为其标识值。因为各个应用程序的名称不相同,所以标识值可以唯一标识各个应用程序。统计当下设备中各个应用程序的名称,发现所占字节数如图1所示。
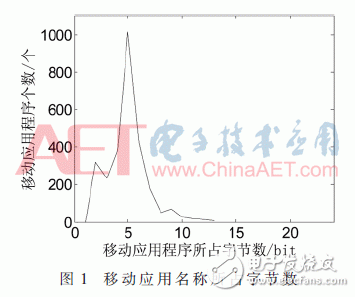
从普遍性的角度,可用72个比特来标识各个应用程序的名称。假设在某个发现周期中,作业应用程序的个数为n,非作业应用程序的个数为m,n≥1,m≥0,那么在发现周期中所涉及到的应用程序的总数为L=n+m,假定应用程序标识值的最大值为M,M=272,那么作业应用程序的分页范围的最大长度就为M,最小长度为1。特定发现周期中的所有分页范围构成分页集合Gp,其互补集合就是未分页区域的值范围。
实际上,发现消息就是经过RLE编码之后的分页集合Gp的标识之一。
2 发现消息设计
本文提出的基于RLE编码的二叉树方法,通过一个经过RLE编码的分页二叉树Tp来唯一地表示这种分布,且一个Tp对应一个Gp[6]。下面介绍具体过程。
2.1 发现消息二叉树的构造
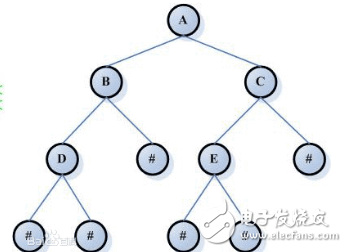
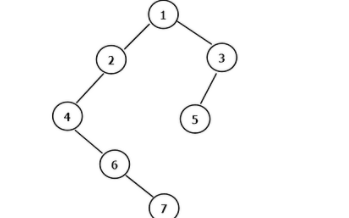
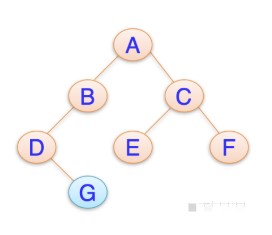
设备在发现周期中可以根据应用程序标识值唯一地创建发现消息二叉树。当通过二叉树表示分页范围时,迭代中点细分法用于将整个值范围[0,M-1]划分为不确定长度的多个节点,如a∈{M,M/2,M/4,M/8,…}。在迭代细分过程中,若每个划分范围只包含非作业的应用程序或作业的应用程序,则结束此过程;若较小(较大)范围不包含作业应用程序和非作业应用程序,则执行较小(较大)范围的中点进行迭代细分。每个细分操作伴随着在现有二叉树上添加一个左(右)节点,并将一个根节点进行初始化。以此类推,直到没有范围包含作业或非作业应用程序后,完成发现消息的二叉树的构造。
基于上述过程,设备可以通过算法1为特定Gp构造一颗二叉树。
算法1:
(1)设置初始搜素范围[x,y],其中x=0,y=M-1,将当前节点设置为根节点;
(2)对于搜索范围[x,y],通过中点二分法分成两部分,分别为[x,(x+y)/2]和[(x+y)/2,y];
(3)若较小(大)范围仅包含作业应用程序标识,则不进行下一步划分。一个叶节点和一个边缘被添加到当前节点的左(右)侧;
(4)若较小(大)范围仅包含非作业的应用程序标识值,则不进行下一步划分。在当前节点的左(右)侧不添加节点;
(5)若较小(大)范围包含两种不同的应用程序标识值,那么进行下一步的划分。在当前节点的左(右)侧添加一个节点和一个边缘,并且将搜索范围改为[x,(x+y)/2]和([(x+y)/2,y]),进行步骤(2)的操作;
(6)若没有范围进一步划分,那么发现消息二叉树构造完成,否则,转到步骤(2)。
2.2 发现消息的构造
为了便于在无线信道中实现D2D通信过程,本文进行了消息二叉树转换二进制比特串的过程。
由2.1节可知,根据节点的度数和连接性可以将节点划分为以下4种不同的类型:
(1)具有左和右子树/叶节点的节点;
(2)只有左子树/叶节点的节点;
(3)只有右子树/叶节点的节点;
(4)叶节点本身。
因此,可以根据表1所示的原理将每个节点用两个比特来表示,并依据二叉树遵循宽度优先的遍历准则,按顺序输出每个节点的两位以形成二进制比特串,随后通过算法2使用的RLE编码将比特串编码为最终的发现消息。
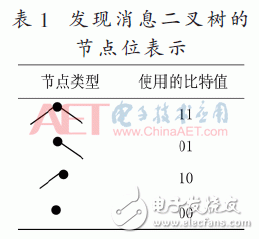
由于该比特串中只含有‘0’和‘1’两种不同的数值,所以可以使用两个字节来进行发现消息的RLE编码的过程。
算法2:
(1)计算比特串长度值,初始化计数变量和位置指针,并读取由算法1生成的比特串;
(2)对比循环读取的值与当前要进行RLE编码的值:
①若相等,计数器加1,位置指针加1,直到不相等的数值出现,按照计数值在前数值在后的规则,进行发现消息的构造,进行步骤(3);
②否则,直接存储该值到发现消息中,并将位置指针加1,进行步骤(3);
(3)若读取到比特串的末尾处,则结束程序;
(4)结束程序,完成发现消息的构造。
由此,设备中的应用程序可以根据发现消息的比特串来判断自身是否被激活。首先,设备通过RLE进行比特串的解码,然后按照宽度优先准则,将比特串转化为一棵二叉树,随后判断设备中的应用程序标识值是否属于由该二叉树表示的集合,仅当其标识值属于该集合时,才可认为含有此应用程序的终端就是目标设备,具体的判断方法如下:
(1)首先,接收到经过RLE编码的比特串;
(2)循环读取当前的数值val,若val≠0且val≠1,则按照此数值将其后的值补充为val进行显示;若val=0或val=1,则按原值显示;
(3)初始化节点的取值范围,起始和结束位置为Start=0和end=0,将当前的判断节点视为根节点;
(4)对于每个当前判断的节点,设备中的应用程序都应判断其标识值是否属于该节点指示的范围;
(5)若当前判断节点为叶节点,则认为设备中的此应用程序是作业的,退出判断过程。否则,设置中点为mid=(Start+end)/2;
(6)如果当前判断的标识值>mid;
①若当前节点的右子树存在,那么设置Start=mid,将其右子树的根节点为当前判断节点,执行步骤(2);
②否则,即不存在右子树,那么设备认为它没有要被作业的应用程序;
(7)如果判断的标识值
①若当前节点的左子树存在,设置end=mid,将该节点的左子树的根节点为当前判断节点,执行步骤(2);
②否则,退出程序;
(8)结束程序。
综上所述,发现消息是被复制到一个二进制比特串中的,这样可以达到减少发现消息大小的目的。同时由于使用比特串,所以即使存在大量的作业应用程序,所提出的方法也不会出现假肯定性错误[4]。而且就其复杂度而言,它与二进制搜索算法一样高效的。
发现消息的理想设计是通过最短的消息发现大量的设备,并且不会出现错误率。基于上述分析,所提出的发现消息可以精确指示多个应用程序。此外,本文所提出的设计性能取决于设备中作业和非作业应用程序的数量。
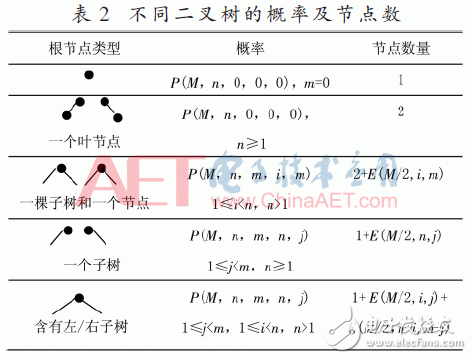
由于分页二叉树上的每个节点由两个比特表示,因此首先分析的是二叉树上的节点的期望数量。假设在[0,M-1]分布范围内有L个应用程序,由于发现消息二叉树是基于应用程序标识值的不同分布而变化的,因此期望函数E(M,n,m)被定义为发现二叉树中的期望节点数,其中M≥n+m,n≥1。根据节点的不同特征,本文采用递归分析的方法计算E(M,n,m)。假设在范围[0,M-1]中存在n个作业和m个非作业应用程序,那么在此情况下构造的特定二叉树的概率被定义为P(M,n,m,i,j),含义:在该特定二叉树中,由根节点的左子树表示的范围包含i个作业和j个非作业应用程序,而由右子树表示的范围内包含n-i个作业和m-j个非作业应用程序。表2给出了不同特定二叉树的节点数和其概率。
那么,二叉树中的总节点数分为一个根节点和左、右子树中节点数的总数。左子树和右子树中的预期节点数可以分别表示为E(M/2,i,j)和E(M/2,n-i,m-j)。
基于统计期望的定义,表2中列出的其他情况也可以以相同的方式来进行分析。对于初始情况,则E(2,1,1)=2和E(M,n,0)=1,其中n≥1,m=0,M>2。
由表2可得发现二叉树的节点统计期望:
由于作业应用程序的数量远小于总的应用程序的数量,本文中,只考虑n≤M/2的情况,对于某个m,m≥n,那么节点数量最大的概率为:
假定消息二叉树的节点数为式(2)中的E(M,n,m),那么该E(M,n,m)所对应的信息如表3所示。
由文献[5]可得,在不失一般性的情况下,假定在比特串中某一位置出现0的概率为p,0≤p≤1,那么出现1的概率为1-p;以此类推,长度为p的0游程出现的概率为pl(1-p),长度为l的1游程出现的概率为p(1-p)l。
在本文中,某一位置出现0的概率为:
比较式(4)、式(5)可得,所提出的方法可以显着减少统计标准中的发现消息大小。这在后续的仿真结果中可以得到进一步的验证。
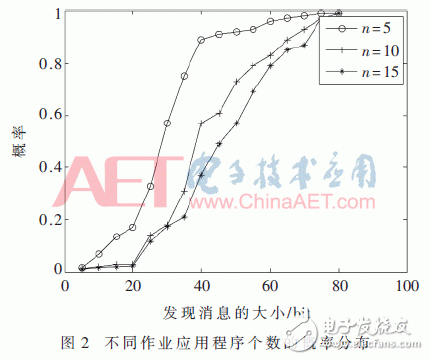
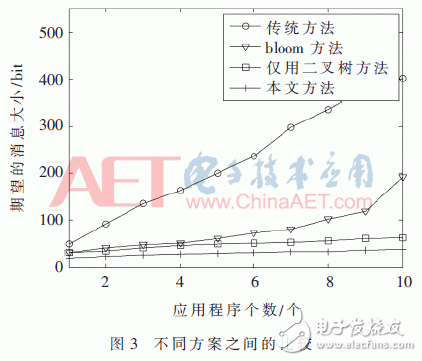
发现消息的大小是实现高效D2D通信的关键问题之一[7],因此本文通过研究发现消息大小的方式来评估所提方法的性能。图2显示了所提方案在不同作业应用程序下的累积分布图,由该图可得在90%的仿真结果中,所提方案可以在较小比特长度的情况下,能够很好地发现作业的应用程序;由图3可以得出,所提方案中的发现消息大小优于其他3种方案。传统方案中,由于发现消息是含有全部应用程序的名称,其大小为72n bit,与传统方案相比,其余3种方案对于发现消息减少方法都实现了显著的增强。而且所提方案相比于bloom方案存在的假肯定性错误和比特个数而言,它的效果显然是更优的。并且本文所提方案在二叉树的基础上又进行了一次RLE编码,更好地实现了缩短发现消息大小的目的。
本文提出了一种通过减少发现消息大小来解决D2D通信系统中发现容量问题的新方法。经过RLE编码的发现消息二叉树被设计为指示作业应用程序的标识范围,这要比传统机制中携带作业应用程序的名称列表更为有效。而且经过理论分析和仿真模拟可得,预期发现消息的大小得以显着减少。因此,本文提出的方法增加了D2D通信系统的发现能力,能够支持大量的设备通信。对于未来的工作,所提出的方案还可以被优化,以便处理消息尺寸超重这一个罕见的情况。
3 性能分析

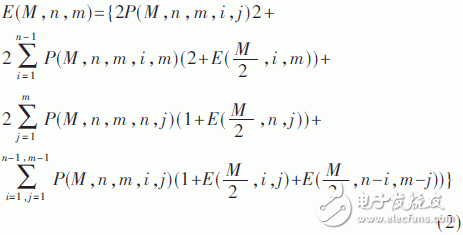
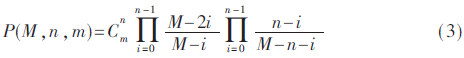


4 结论
-
编码
+关注
关注
6文章
957浏览量
54934 -
5G
+关注
关注
1356文章
48503浏览量
565735 -
D2D
+关注
关注
2文章
16浏览量
7231
发布评论请先 登录
相关推荐
基于二叉树的时序电路测试序列设计
二叉树层次遍历算法的验证
基于二叉树的算术编码二值化方法
二叉树操作的相关知识和代码详解




 关于D2D通信中基于RLE编码二叉树发现消息的设计
关于D2D通信中基于RLE编码二叉树发现消息的设计










评论