摘要:
由于船舶动力定位控制系统是一个复杂的非线性系统,常规整定的PID参数难以取得理想的控制效果,由此提出将免疫类电磁机制(IEM)算法用于PID控制器的参数自整定。针对类电磁机制(EM)算法易陷入局部最优的缺陷,引入免疫信息处理机制,利用其特有的浓度选择机制保留优良的粒子并通过免疫算子使粒子靠近最优位置。使用IEM、EM和PSO算法整定PID控制器参数,分析结果可以得出IEM算法具有更优的稳定性、更高的收敛精度。最后在IEM-PID和常规PID控制器作用下分别对船舶DP的位置和艏向进行仿真,仿真结果表明,相比常规PID控制器,IEM-PID控制器响应速度更快、稳定性更优、稳态误差更小。
0 引言
近年来我国船舶工业和海洋事业处在高速发展期,船舶动力定位仍是一大研究热点。与传统的锚泊定位相比,动力定位因其定位精度高、机动性强且不受水深限制等优点,在海洋开发中备受青睐[1]。PID控制器作为最早被应用在船舶动力定位系统上的控制器,对于DP船舶控制精度要求特别高的系统,效果并不理想。最先应用于PID自整定的算法是Z-N PID整定法[2],随后神经网络[3]、遗传算法[4]、粒子群算法[5]等一系列算法都较好地提高了PID控制的适应性,但也存在许多不足,如控制易出现超调、振荡激烈或者策略复杂等。
类电磁机制(Electromagnetism-like Mechanism,EM)算法是由Birbil和Fang在2003年首次提出的一种基于人工智能的随机全局优化算法。该算法的优势在于具有简单的寻优机理、响应速度快、所需资源较少因而容易实现等,但是算法运行后期也存在会陷入局部最优的缺陷。为此,姜建国等人采用混沌-模式搜索方法,能有效跳出局部极值点进行局部搜索,但其搜索结果的好坏很大程度上依赖于初始点的选择[6];TAN J D等人提出了SPC的新搜索方案,设计一个非线性方程式,根据每次迭代中比较段的结果动态调整探针长度跳出局部最优,但是算法结构复杂,运行成本大大增加[7]。
针对以上问题,本文提出一种免疫类电磁机制(Immune Electromagnetism-like Mechanism,IEM)算法。PID控制器kp、ki、kd3个参数由IEM算法进行自整定,并与EM算法和粒子群优化(PSO)算法的仿真结果进行比较,验证了IEM算法的有效性。最后将基于IEM算法的船舶动力定位PID控制器进行仿真,仿真结果表明改进过后的控制器具有更好的控制效果。
1 船舶运动模型
1.1 船舶运动数学模型
船舶处于航向保持、航迹保持的操纵运动和动力定位中的定点位置保持时,可认为船舶只作三自由度的平面运动[8]。当只执行位置保持功能时速度值很小,科氏向心力和非线性阻尼可以忽略[9]。所以船舶动力定位低频运动数学模型为:

1.2 动力定位控制对象模型
现以一艘拖轮为受控对象,船舶参数如表1所示,附加质量的惯性矩阵和阻尼矩阵分别为:
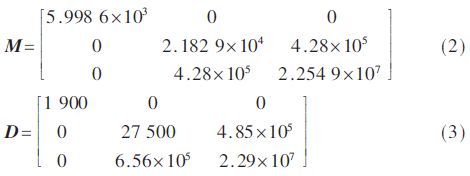
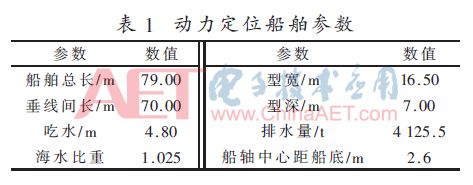
在动力定位系统中,由常规试凑法得到的三自由度PID控制参数为:
纵荡:kp=156.07,ki=0.38,kd=115.78
橫荡:kp=114.15,ki=0.01,kd=175.87
艏摇:kp=4 645.43,ki=1.561,kd=147 127.54
由于常规PID控制器难以达到理想的控制效果,因此需要对PID控制参数进行整定。
2 IEM算法整定PID参数
2.1 EM算法
EM算法分成4个步骤,即初始化、局部搜索、计算合力和移动粒子[10]。带电粒子xi在EM算法中电荷量的计算公式如下:

2.2 IEM算法
为了解决EM算法后期容易陷入局部最优的缺陷,将生物免疫机制引入到算法中。该机制中,抗原代表了求解问题的目标函数,而抗体代表了问题的解[11-12]。在每次迭代过程中,除了EM算法的更新公式内产生N个粒子,还随机生成满足约束条件的M个粒子,以此来增加粒子的多样性。采用基于浓度机制的多样性保持策略,使得新一代粒子群体中各适应度层次的粒子维持一定的浓度。第i个粒子(抗体)的浓度定义为:

式(9)中粒子i被选中的概率和与该粒子相似的粒子数量成反比,其意义就在于即使粒子对应的适应度值较低,也有机会得到进化,从而保证了群体的多样性。
IEM算法的实现步骤如下:
(1)确定IEM算法的参数值,包括:种群规模N、种群维度n、最大迭代次数Maxgeneration、最小适应值minfit;
(2)随机生成N个粒子,形成初始种群,根据适应度函数计算出种群的适应值,将当前目标函数值f(xi)最优的粒子记为xbest;
(3)对最优粒子进行局部搜索;
(4)利用式(4)和式(5)分别计算出粒子的电荷量以及粒子间的作用力;
(5)根据式(6)移动粒子,找出粒子位置更新后的最优粒子,并将对应的位置粒子存入记忆库;
(6)随机生成M个粒子,同步骤(2),根据式(9)从N+M个粒子中依据选取概率大小来选取N个粒子;
(7)根据最小适应值和最大迭代次数判断是否迭代结束,并输出符合条件的最优粒子,否则转至步骤(3)。
2.3 IEM算法性能分析
本文选用两个具有不同特征的典型测试函数对改进后的算法进行测试,来验证IEM算法的优越性:
(1)Schwefel函数:
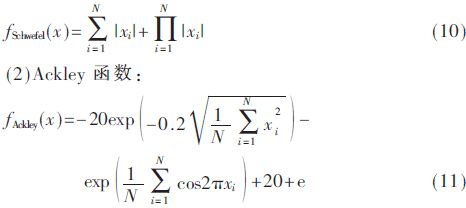
具体参数设置如下:种群规模N=20,种群维度n=10,最大迭代次数Maxgeneration=500,标准PSO算法中学习因子c1=c2=2,惯性因子ω=1。
图1为两个测试函数在不同算法优化后绘制成的迭代曲线。从图中可以看出,IEM算法无论在单峰Schwefel函数还是多峰Ackley函数中都具有较快的收敛速度。
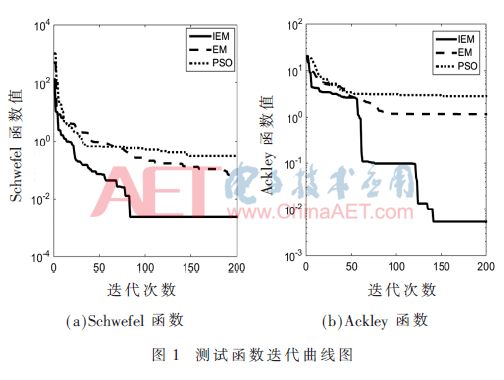
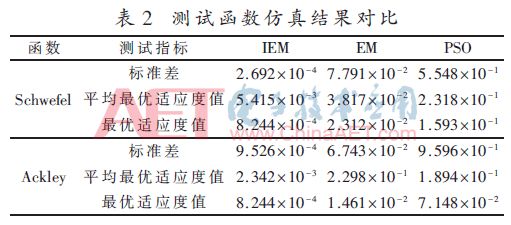
表2为优化的结果数据,测试指标中的标准差可以用来评估算法的稳定性,而最优适应值和平均最优适应值可以用来分析算法的精度。从表中可以看出,IEM算法相比EM和PSO算法,在不同测试指标上均有数量级上的提升,因此IEM算法的稳定性更优,收敛精度更高。
2.4 IEM算法整定PID控制参数
本文分别用IEM算法、EM算法以及PSO算法对PID的参数进行了寻优,并通过时域性能指标来比较各算法寻优过后的阶跃响应。适应度函数选用ITAE指标:

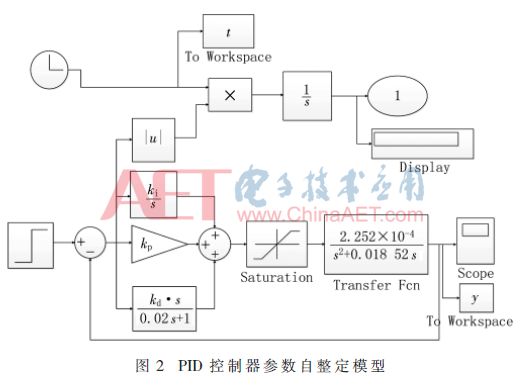
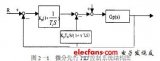
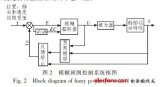
以拖轮纵荡作为被控对象,在Simulink环境下建立的模型如图2所示。图中,输出端口1为式(12)所示的ITAE指标。在PID参数自整定过程中,将控制器的一组三维参数(kp,ki,kd)作为IEM算法的一个粒子,PID参数的整定转换为三维粒子的函数优化问题,通过IEM随机产生的粒子,依次对应各组参数,运行Simulink模型后可以得到各组参数的性能指标,并将其传递到IEM算法中对应粒子的适应度值。
仿真实验中,IEM算法参数选取如下:种群规模N=50,最大迭代次数Maxgeneration=100,种群维度n=3,最小适应值minfit=0.1;标准PSO算法中学习因子c1=c2=2,惯性因子ω=0.6。
表3列出了IEM、EM、PSO 3种算法整定过后的kp、ki和kd参数及性能指标。可以看出,IEM算法对PID控制器参数进具有更好的整定效果。
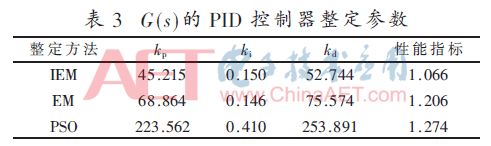
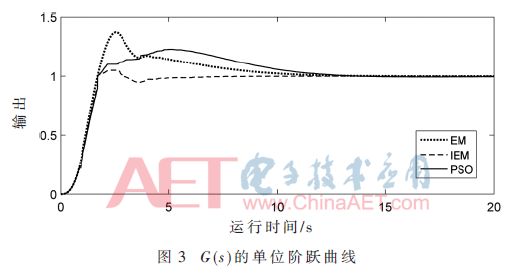
图3为IEM、EM、PSO 3种算法在控制对象G(s)的单位阶跃响应曲线。由图可知,采用IEM算法整定的PID控制器具有较快的响应速度、较短的调节时间,且超调和稳态误差也最小。
3 IEM-PID动力定位控制器仿真分析
以拖轮为对象,利用IEM算法对PID控制器的参数进行整定。取种群规模N=50,种群维度n=3,最大迭代次数Maxgeneration=100,最小适应值minfit=0.1。控制参数整定结果为:
纵荡:kp=45.22,ki=0.15,kd=52.74
橫荡:kp=55.13,ki=0.026,kd=76.62
艏摇:kp=3 976.78,ki=1.237,kd=131 799.54
为验证所设计的IEM-PID控制器性能,将其控制船舶三自由度运动效果,并与传统PID控制器在相同情况下进行对比。船舶起始位置为η=[0,0,0],给定船舶的期望位置为η=[20,30,10],仿真时间为500 s,仿真结果如图4所示。
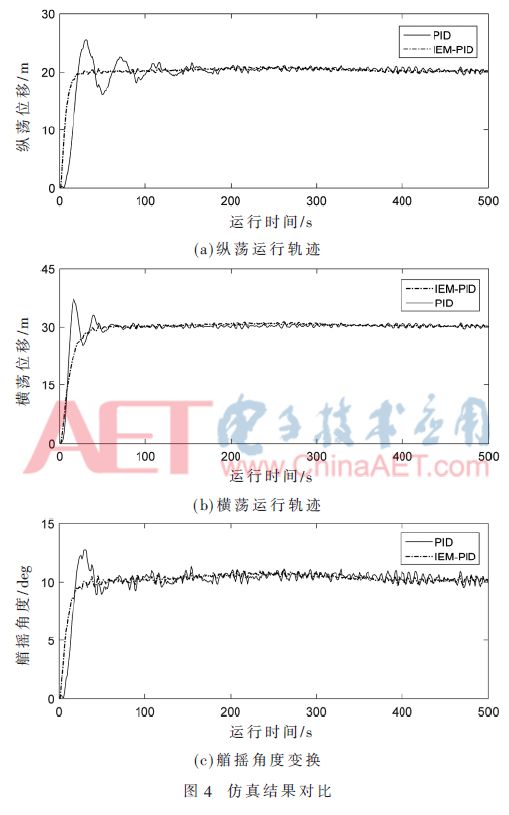
由图4仿真结果可知,传统PID控制在纵荡、横荡、艏摇3个方向上响应的调节时间和超调量分别为123 s、61 s、58 s和30.24%、23.33%、29.3%。IEM-PID在这3个方向的调节时间分别为21 s、38 s、27 s,且在3个方向的响应曲线无超调。可见,IEM-PID控制器在调节时间、超调量以及稳态精度上都有显著提高,不仅能够满足控制需求,而且其控制效果也比传统PID更加优越。
4 结论
控制器的控制效果决定着船舶动力定位系统的精度和稳定性。IEM-PID控制器中的免疫类电磁机制算法基于浓度选择机制的粒子选择策略保留优良粒子,防止了算法优化性能退化。仿真结果表明,改进后的控制器在较大程度上提高了控制系统性能,有一定的实用价值。
-
控制器
+关注
关注
112文章
16474浏览量
179676 -
定位系统
+关注
关注
10文章
588浏览量
36546 -
PID
+关注
关注
36文章
1473浏览量
85893
原文标题:【学术论文】基于IEM的动力定位PID控制器参数整定
文章出处:【微信号:ChinaAET,微信公众号:电子技术应用ChinaAET】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
基于遗传算法的PID 控制及其MATLAB 仿真
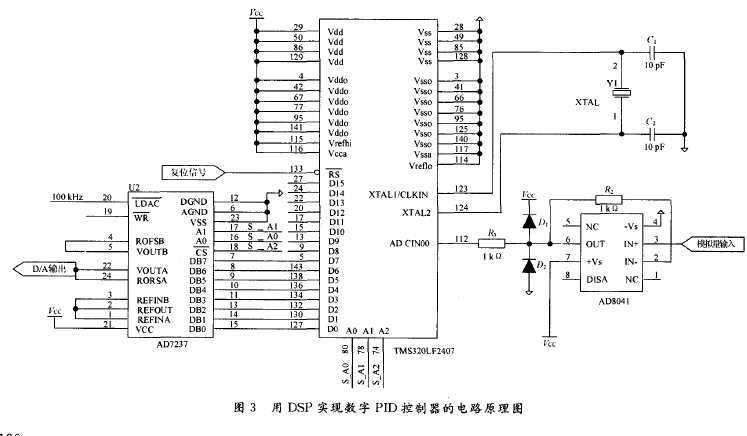
如何使用DSP进行数字PID控制器的设计
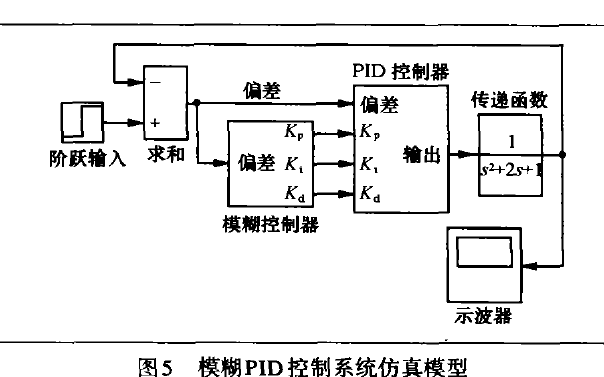
如何使用MTALAB的模糊PID控制器进行设计与仿真的研究
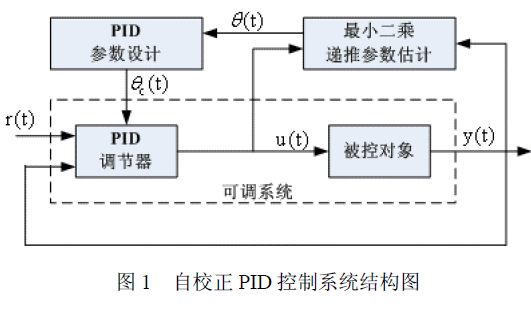
如何才能实现自校正PID控制器详细资料与仿真分析




 基于IEM算法的船舶动力定位PID控制器进行仿真
基于IEM算法的船舶动力定位PID控制器进行仿真











评论