所有的机器学习算法都或多或少的依赖于对目标函数最大化或者最小化的过程。我们常常将最小化的函数称为损失函数,它主要用于衡量模型的预测能力。在寻找最小值的过程中,我们最常用的方法是梯度下降法,这种方法很像从山顶下降到山谷最低点的过程。
虽然损失函数描述了模型的优劣为我们提供了优化的方向,但却不存在一个放之四海皆准的损失函数。损失函数的选取依赖于参数的数量、局外点、机器学习算法、梯度下降的效率、导数求取的难易和预测的置信度等方面。这篇文章将介绍各种不同的损失函数,并帮助我们理解每种函数的优劣和适用范围。
由于机器学习的任务不同,损失函数一般分为分类和回归两类,回归会预测给出一个数值结果而分类则会给出一个标签。这篇文章主要集中于回归损失函数的分析。
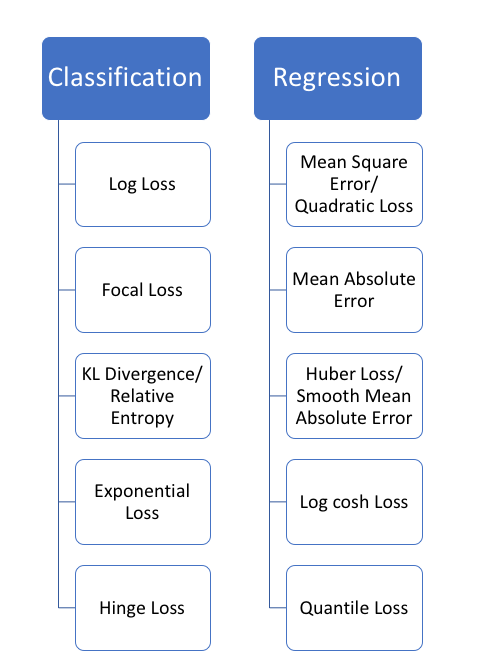
1.均方误差、平方损失——L2损失
均方误差(MSE)是回归损失函数中最常用的误差,它是预测值与目标值之间差值的平方和,其公式如下所示:
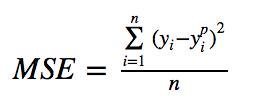
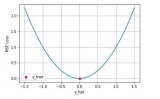
下图是均方根误差值的曲线分布,其中最小值为预测值为目标值的位置。我们可以看到随着误差的增加损失函数增加的更为迅猛。
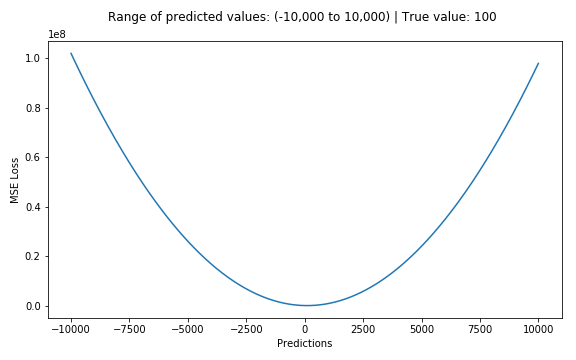
2.平均绝对误差——L1损失函数
平均绝对误差(MAE)也是一种常用的回归损失函数,它是目标值与预测值之差绝对值的和,表示了预测值的平均误差幅度,而不需要考虑误差的方向(注:平均偏差误差MBE则是考虑的方向的误差,是残差的和),其公式如下所示:
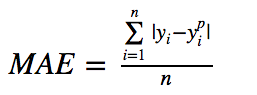
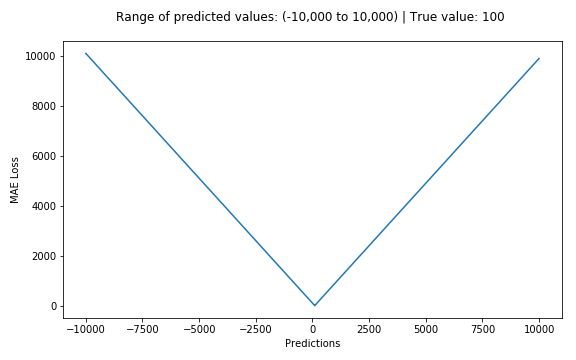
平均绝对误差和均方误差(L1&L2)比较
通常来说,利用均方差更容易求解,但平方绝对误差则对于局外点更鲁棒,下面让我们对这两种损失函数进行具体的分析。
无论哪一种机器学习模型,目标都是找到能使目标函数最小的点。在最小值处每一种损失函数都会得到最小值。但哪种是更好的指标呢?让我们用具体例子看一下,下图是均方根误差和平均绝对误差的比较(其中均方根误差的目的是与平均绝对误差在量级上统一):
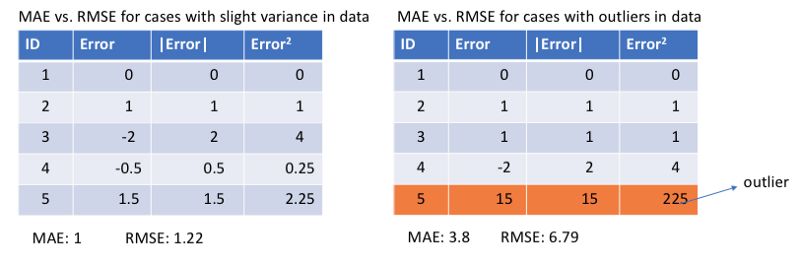
左边的图中预测值与目标值很接近,误差与方差都很小,而右边的图中由于局外点的存在使得误差变得很大。
由于均方误差(MSE)在误差较大点时的损失远大于平均绝对误差(MAE),它会给局外点赋予更大的权重,模型会致力减小局外点造成的误差,从而使得模型的整体表现下降。
所以当训练数据中含有较多的局外点时,平均绝对误差(MAE)更为有效。当我们对所有观测值进行处理时,如果利用MSE进行优化则我们会得到所有观测的均值,而使用MAE则能得到所有观测的中值。与均值相比,中值对于局外点的鲁棒性更好,这就意味着平均绝对误差对于局外点有着比均方误差更好的鲁棒性。
但MAE也存在一个问题,特别是对于神经网络来说,它的梯度在极值点处会有很大的跃变,及时很小的损失值也会长生很大的误差,这不利于学习过程。为了解决这个问题,需要在解决极值点的过程中动态减小学习率。MSE在极值点却有着良好的特性,及时在固定学习率下也能收敛。MSE的梯度随着损失函数的减小而减小,这一特性使得它在最后的训练过程中能得到更精确的结果。
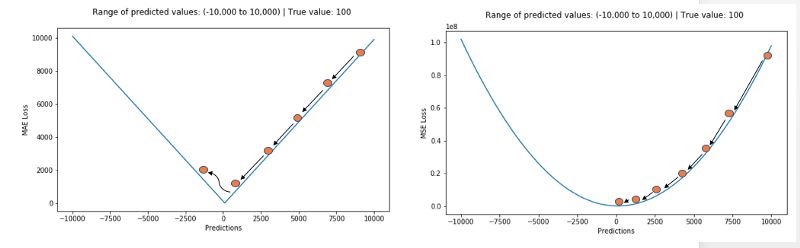
在实际训练过程中,如果局外点对于实际业务十分重要需要进行检测,MSE是更好的选择,而如果在局外点极有可能是坏点的情况下MAE则会带来更好的结果。(注:L1和L2一般情况下与MAE和MSE性质相同)
总结:L1损失对于局外点更鲁棒,但它的导数不连续使得寻找最优解的过程低效;L2损失对于局外点敏感,但在优化过程中更为稳定和准确。
但现实中还存在两种损失都很难处理的问题。例如某个任务中90%的数据都符合目标值——150,而其余的10%数据取值则在0-30之间。那么利用MAE优化的模型将会得到150的预测值而忽略的剩下的10%(倾向于中值);而对于MSE来说由于局外点会带来很大的损失,将使得模型倾向于在0-30的方向取值。这两种结果在实际的业务场景中都是我们不希望看到的。
那怎么办呢?
让我们来看看其他的损失函数吧!
3.Huber损失——平滑平均绝对误差
Huber损失相比于平方损失来说对于局外点不敏感,但它同样保持了可微的特性。它基于绝对误差但在误差很小的时候变成了平方误差。我们可以使用超参数δ来调节这一误差的阈值。当δ趋向于0时它就退化成了MAE,而当δ趋向于无穷时则退化为了MSE,其表达式如下,是一个连续可微的分段函数:
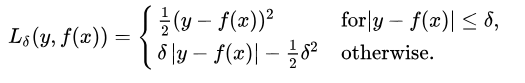
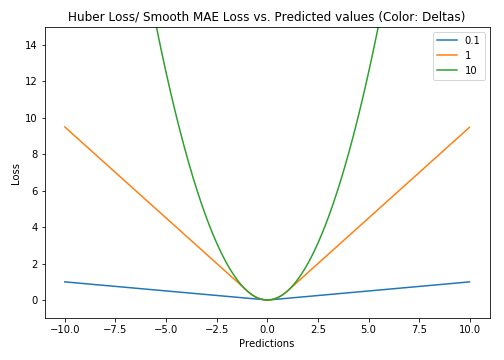
对于Huber损失来说,δ的选择十分重要,它决定了模型处理局外点的行为。当残差大于δ时使用L1损失,很小时则使用更为合适的L2损失来进行优化。
Huber损失函数克服了MAE和MSE的缺点,不仅可以保持损失函数具有连续的导数,同时可以利用MSE梯度随误差减小的特性来得到更精确的最小值,也对局外点具有更好的鲁棒性。
但Huber损失函数的良好表现得益于精心训练的超参数δ。
4.Log-Cosh损失函数
对数双曲余弦是一种比L2更为平滑的损失函数,利用双曲余弦来计算预测误差:
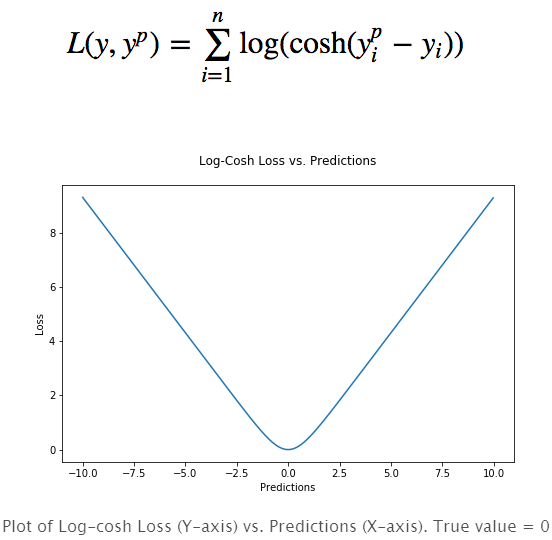
其优点在于对于很小的误差来说log(cosh(x))与(x**2)/2很相近,而对于很大的误差则与abs(x)-log2很相近。这意味着logcosh损失函数可以在拥有MSE优点的同时也不会受到局外点的太多影响。它拥有Huber的所有优点,并且在每一个点都是二次可导的。二次可导在很多机器学习模型中是十分必要的,例如使用牛顿法的XGBoost优化模型(Hessian矩阵)。

但是Log-cosh损失并不是完美无缺的,它还是会在很大误差的情况下梯度和hessian变成了常数。
5.分位数损失(Quantile Loss)
在大多数真实世界的预测问题中,我们常常希望得到我们预测结果的不确定度。通过预测出一个取值区间而不是一个个具体的取值点对于具体业务流程中的决策至关重要。
分位数损失函数在我们需要预测结果的取值区间时是一个特别有用的工具。通常情况下我们利用最小二乘回归来预测取值区间主要基于这样的假设:取值残差的方差是常数。但很多时候对于线性模型是不满足的。这时候就需要分位数损失函数和分位数回归来拯救回归模型了。它对于预测的区间十分敏感,即使在非常数非均匀分布的残差下也能保持良好的性能。下面让我们用两个例子看看分位数损失在异方差数据下的回归表现。
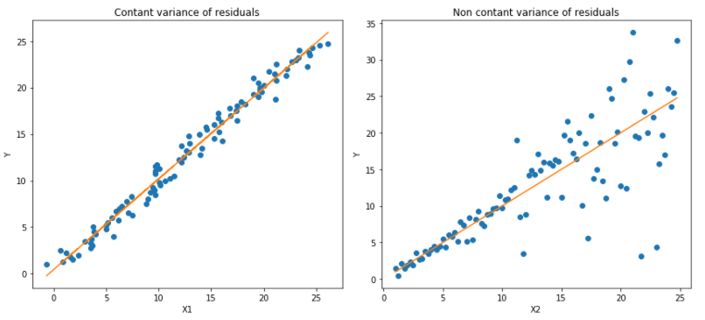
上图是两种不同的数据分布,其中左图是残差的方差为常数的情况,而右图则是残差的方差变化的情况。我们利用正常的最小二乘对上述两种情况进行了估计,其中橙色线为建模的结果。但是我们却无法得到取值的区间范围,这时候就需要分位数损失函数来提供。
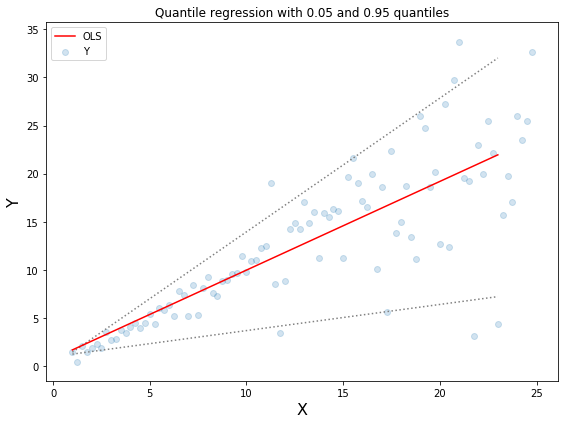
上图中上下两条虚线基于0.05和0.95的分位数损失得到的取值区间。从图中可以清晰地看到建模后预测值得取值范围。分位数回归的目标在于估计给定预测值的条件分位数。实际上分位数回归就是平均绝对误差的一种拓展(当分位数为第50个百分位时其值就是平均绝对误差)
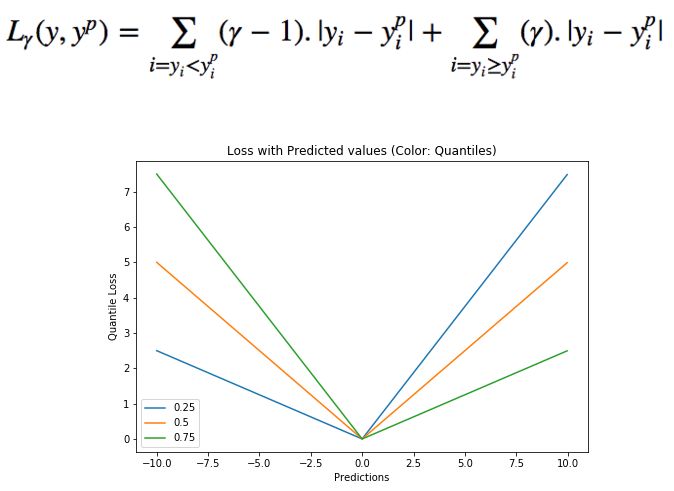
分位数值得选择在于我们是否希望让正的或者负的误差发挥更大的价值。损失函数会基于分位数γ对过拟合和欠拟合的施加不同的惩罚。例如选取γ为0.25时意味着将要惩罚更多的过拟合而尽量保持稍小于中值的预测值。γ的取值通常在0-1之间,图中描述了不同分位数下的损失函数情况,明显可以看到对于正负误差不平衡的状态。
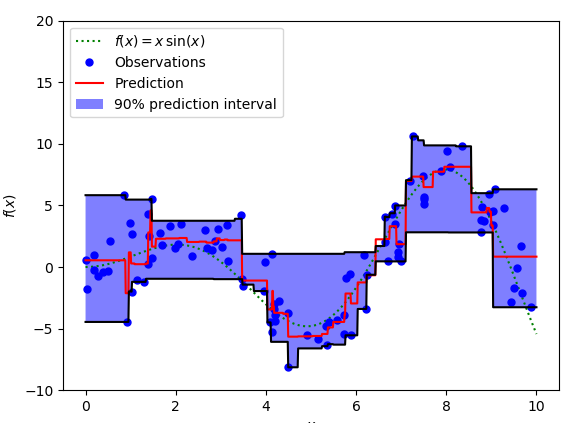
我们可以利用分位数损失函数来计算出神经网络或者树状模型的区间。下图是计算出基于梯度提升树回归器的取值区间。90%的预测值起上下边界分别是用γ值为0.95和0.05计算得到的。
在文章的最后,我们利用sinc(x)模拟的数据来对不同损失函数的性能进行了比较。在原始数据的基础上加入而高斯噪声和脉冲噪声(为了描述鲁棒性)。下图是GBM回归器利用不同的损失函数得到的结果,其中ABCD图分别是MSE,MAE,Huber,Quantile损失函数的结果:
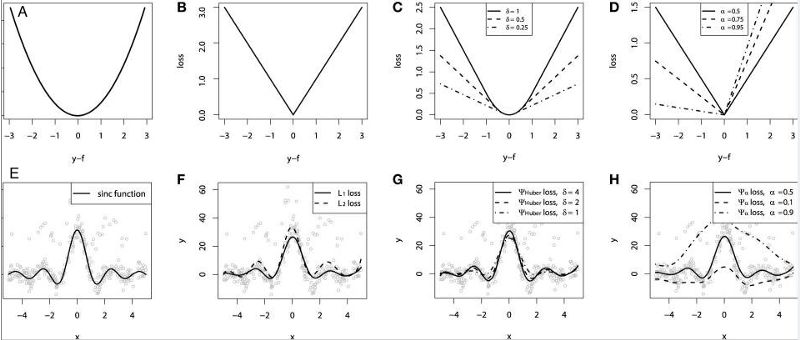
我们可以看到MAE损失函数的预测值受到冲击噪声的影响更小,而MSE则有一定的偏差;Huber损失函数对于超参数的选取不敏感,同时分位数损失在对应的置信区间内给出了较好的估计结果。
希望小伙伴们能从这篇文章中更深入地理解损失函数,并在未来的工作中选择合适的函数来更好更快地完成工作任务。
最后,附上本文中几种损失函数的简图,回味一番:
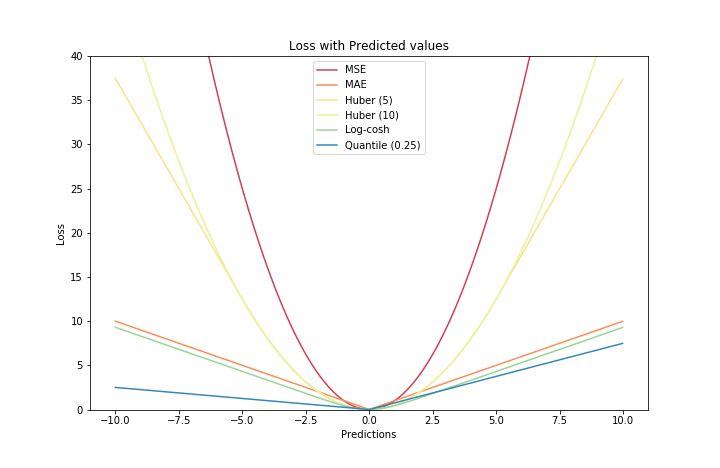
-
函数
+关注
关注
3文章
4351浏览量
63243 -
机器学习
+关注
关注
66文章
8459浏览量
133362
原文标题:机器学习里必备的五种回归损失函数
文章出处:【微信号:thejiangmen,微信公众号:将门创投】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
如何使用Arm CMSIS-DSP实现经典机器学习库
神经网络中的损失函数层和Optimizers图文解读
机器学习实用指南:训练和损失函数




 机器学习经典损失函数比较
机器学习经典损失函数比较











评论