NP完全性理论与近似算法

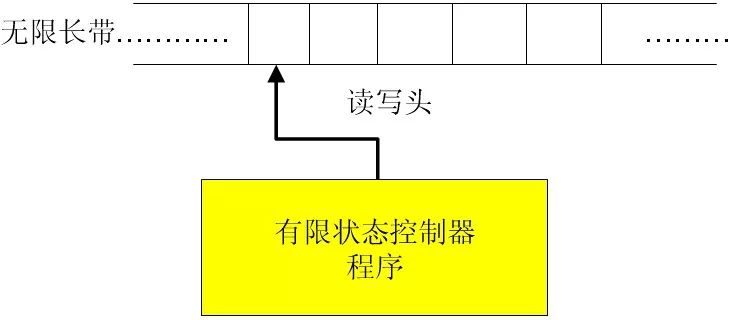
一、图灵机

根据有限状态控制器的当前状态及每个读写头读到的带符号，图灵机的一个计算步可实现下面3个操作之一或全部。

改变有限状态控制器中的状态。

清除当前读写头下的方格中原有带符号并写上新的带符号。

独立地将任何一个或所有读写头，向左移动一个方格(L)或向右移动一个方格(R)或停在当前单元不动(S)。

k带图灵机可形式化地描述为一个7元组(Q，T，I，δ，b，q0，qf)，其中:

Q是有限个状态的集合。

T是有限个带符号的集合。

I是输入符号的集合。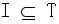

b是唯一的空白符，b∈T-I。

q0是初始状态。

qf是终止(或接受)状态。

δ是移动函数。

它是从Q×Tk的某一子集映射到Q×(T×{L，R，S})k的函数。

图灵机M的时间复杂性T(n)是它处理所有长度为n的输入所需的最大计算步数。如果对某个长度为n的输入，图灵机不停机，T(n)对这个n值无定义。

图灵机的空间复杂性S(n)是它处理所有长度为n的输入时，在k条带上所使用过的方格数的总和。如果某个读写头无限地向右移动而不停机，S(n)也无定义。

确定型图灵机

有限状态集Q，状态q0:初始状态；qy：接受状态；状态qn：不接受状态。

字符集合{0, 1, b} ；其中b是空格符。

转换功能：

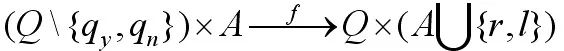
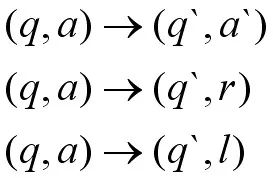
输入x = 101000b

执行顺序：

q0输入1 （q0,r）右移磁头到0

q0输入0 （q0,r）右移磁头到1

q0输入0 （q0,r）右移磁头到0

...

q0输入b （q1,l）左移磁头到0

q1输入0 （q2,b）

q2输入b （q2,l）左移磁头到0

q2输入0 （q3,b）

q3输入b （qy，l）退出

二、P类与NP类问题

一般地说，将可由多项式时间算法求解的问题看作是易处理的问题，而将需要超多项式时间才能求解的问题看作是难处理的问题。

有许多问题，从表面上看似乎并不比排序或图的搜索等问题更困难，然而至今人们还没有找到解决这些问题的多项式时间算法，也没有人能够证明这些问题需要超多项式时间下界。

在图灵机计算模型下，这类问题的计算复杂性至今未知。

为了研究这类问题的计算复杂性，人们提出了另一个能力更强的计算模型，即非确定性图灵机计算模型，简记为NDTM(Nondeterministic Turing Machine)。

在非确定性图灵机计算模型下，许多问题可以在多项式时间内求解。

非确定性图灵机

在图灵机计算模型中，移动函数δ是单值的，即对于Q´Tk中的每一个值，当它属于δ的定义域时，Q´(T´{L，R，S})k中只有唯一的值与之对应，称这种图灵机为确定性图灵机，简记为DTM(Deterministic Turing Machine)。

非确定性图灵机(NDTM）：一个k带的非确定性图灵机M是一个7元组：(Q，T，I，δ，b，q0，qf)。与确定性图灵机不同的是非确定性图灵机允许移动函数δ具有不确定性，即对于Q×Tk中的每一个值(q;x1,x2,…,xk)，当它属于δ的定义域时，Q×(T×{L，R，S})k中有唯一的一个子集δ(q;x1,x2,…,xk)与之对应。可以在δ(q;x1,x2,…,xk)中随意选定一个值作为它的函数值。

P类与NP类语言定义

P={L|L是一个能在多项式时间内被一台DTM所接受的语言}

NP={L|L是一个能在多项式时间内被一台NDTM所接受的语言}

由于一台确定性图灵机可看作是非确定性图灵机的特例，所以可在多项式时间内被确定性图灵机接受的语言也可在多项式时间内被非确定性图灵机接受。故P Í NP。

NP类语言举例——无向图的团问题

该问题的输入是一个有n个顶点的无向图G=(V，E)和一个整数k。要求判定图G是否包含一个k顶点的完全子图(团)，即判定是否存在V’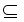V，|V’|=k，且对于所有的u，v∈V’，有(u，v)∈E。

若用邻接矩阵表示图G，用二进制串表示整数k，则团问题的一个实例可以用长度为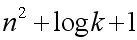的二进位串表示。因此，团问题可表示为语言：

CLIQUE={w#v|w，v∈{0，1}*，以w为邻接矩阵的图G有一个k顶点的团，其中v是k的二进制表示。}

接受该语言CLIQUE的非确定性算法：用非确定性选择指令选出包含k个顶点的候选顶点子集V，然后确定性地检查该子集是否是团问题的一个解。算法分为3个阶段

算法的第一阶段将输入串w#v分解，并计算出n =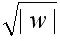 ，以及用v表示的整数k。若输入不具有形式w#v或|w|不是一个平方数就拒绝该输入。显而易见，第一阶段可在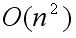时间内完成。

在算法的第二阶段中，非确定性地选择V的一个k元子集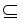V’V。

算法的第三阶段是确定性地检查V’的团性质。若V’是一个团则接受输入，否则拒绝输入。这显然可以在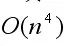时间内完成。因此，整个算法的时间复杂性为 。

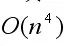非确定性算法在多项式时间内接受语言CLIQUE，故CLIQUE∈NP.

NP完全问题

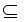PNP。

直观上看，P类问题是确定性计算模型下的易解问题类，而NP类问题是非确定性计算模型下的易验证问题类。

大多数的计算机科学家认为NP类中包含了不属于P类的语言，即P≠NP。

NP完全问题有一种令人惊奇的性质，即如果一个NP完全问题能在多项式时间内得到解决，那么NP中的每一个问题都可以在多项式时间内求解，即P = NP。

目前还没有一个NP完全问题有多项式时间算法。

三、NP完全问题的近似算法

迄今为止，所有的NP完全问题都还没有多项式时间算法。

对于这类问题，通常可采取以下几种解题策略。

只对问题的特殊实例求解

用动态规划法或分支限界法求解

用概率算法求解

只求近似解

用启发式方法求解

近似算法的性能

若一个最优化问题的最优值为c*，求解该问题的一个近似算法求得的近似最优解相应的目标函数值为c，则将该近似算法的性能比定义为

。

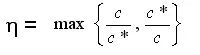
在通常情况下，该性能比是问题输入规模n的一个函数ρ(n)，即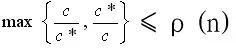

该近似算法的相对误差定义为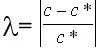：。若对问题的输入规模n，有一函数ε(n)使得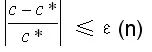则称ε(n)为该近似算法的相对误差界。近似算法的性能比ρ(n)与相对误差界ε(n)之间显然有如下关系：。

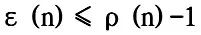旅行售货员问题近似算法

问题描述：给定一个完全无向图G=(V,E)，其每一边(u,v)∈E有一非负整数费用c(u,v)。要找出G的最小费用哈密顿回路。

旅行售货员问题的一些特殊性质：

比如，费用函数c往往具有三角不等式性质，即对任意的3个顶点u,v,w∈V，有：c(u,w)≤c(u,v)+c(v,w)。当图G中的顶点就是平面上的点，任意2顶点间的费用就是这2点间的欧氏距离时，费用函数c就具有三角不等式性质。

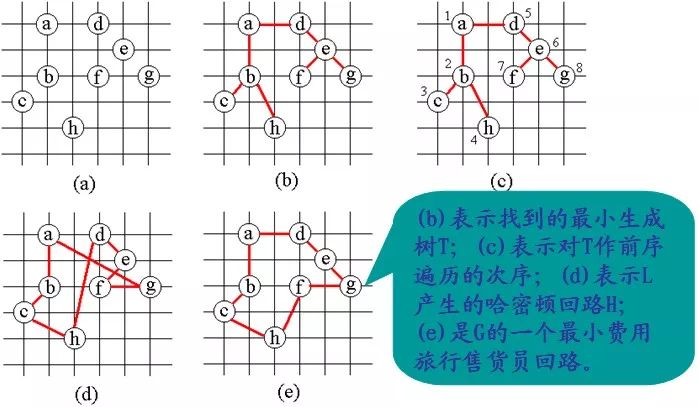
1 满足三角不等式的旅行售货员问题

对于给定的无向图G，可以利用找图G的最小生成树的算法设计找近似最优的旅行售货员回路的算法。

void approxTSP (Graph g)

{

选择g的任一顶点r；

用Prim算法找出带权图g的一棵以r为根的最小生成树T；

前序遍历树T得到的顶点表L；

将r加到表L的末尾，按表L中顶点次序组成回路H，作为计 算结果返回；

}

当费用函数满足三角不等式时，算法找出的旅行售货员回路的费用不会超过最优旅行售货员回路费用的2倍。

实现

/* 主题：近似算法——旅行售货员问题

* 作者：chinazhangjie

* 邮箱：[e-mail]

* 开发语言：C++

* 开发环境：Virsual Studio2005

* 时间: 2010.12.06

*/

#include

#include

#include

using namespace std;

structTreeNode

{

public:

TreeNode(intnVertexIndexA = 0,intnVertexIndexB = 0,intnWeight = 0)

: m_nVertexIndexA(nVertexIndexA),

m_nVertexIndexB(nVertexIndexB),

m_nWeight(nWeight)

{}

public:

intm_nVertexIndexA;

intm_nVertexIndexB;

intm_nWeight;

};

classMST_Prim

{

public:

MST_Prim()

{}

MST_Prim(const vector >& vnGraph)

{

m_nvGraph = vnGraph;

m_nNodeCount = (int)m_nvGraph.size();

}

void SetData(const vector >& vnGraph)

{

m_nvGraph = vnGraph;

m_nNodeCount = (int)m_nvGraph.size();

}

//

const vector& GetMSTree()const

{

returnm_tnMSTree;

}

//

const vector >& GetGraph()const

{

returnm_nvGraph;

}

void DoPrim()

{

// 是否被访问标志

vector bFlag(m_nNodeCount,false);

bFlag[0] = true;

intnMaxIndexA;

intnMaxIndexB;

intj = 0;

while(j < m_nNodeCount - 1){

intnMaxWeight = numeric_limits::max();

// 找到当前最短路径

inti = 0;

while(i < m_nNodeCount){

if(!bFlag[i]){

++ i;

continue;

}

for(intj = 0;j < m_nNodeCount; ++ j){

if(!bFlag[j] && nMaxWeight > m_nvGraph[i][j]){

nMaxWeight = m_nvGraph[i][j];

nMaxIndexA = i;

nMaxIndexB = j;

}

}

++ i;

}

bFlag[nMaxIndexB] = true;

m_tnMSTree.push_back(TreeNode(nMaxIndexA,nMaxIndexB,nMaxWeight));

++ j;

}

// 输出结果

/*for(vector::const_iterator ite = m_tnMSTree.begin();

ite != m_tnMSTree.end();

++ ite){

cout << (*ite).m_nVertexIndexA << "->"

<< (*ite).m_nVertexIndexB << " : "

<< (*ite).m_nWeight << endl;

}*/

}

private:

vector > m_nvGraph;// 无向连通图

vectorm_tnMSTree;// 最小生成树

intm_nNodeCount;

};

classAA_TSP

{

public:

AA_TSP(const vector >& vnGraph)

{

m_mstPrim.SetData(vnGraph);

}

void Get_AA_Path()

{

m_mstPrim.DoPrim();

vectormstree = m_mstPrim.GetMSTree();

vector >graph = m_mstPrim.GetGraph();

intiweight = 0;

for(vector::const_iterator ite = mstree.begin();

ite != mstree.end();

++ ite){

cout << (*ite).m_nVertexIndexA << "->"

<< (*ite).m_nVertexIndexB << " : "

<< (*ite).m_nWeight << endl;

iweight += (*ite).m_nWeight;

}

cout << mstree[mstree.size()-1].m_nVertexIndexB << "->"

<< mstree[0].m_nVertexIndexA << " : "

<< graph[mstree[0].m_nVertexIndexA][mstree[mstree.size()-1].m_nVertexIndexB]

<< endl;

iweight += graph[mstree[0].m_nVertexIndexA][mstree[mstree.size()-1].m_nVertexIndexB];

cout << "Total weight: " << iweight  << endl;

}

private:

MST_Primm_mstPrim;

};

intmain()

{

const intcnNodeCount = 5;

vector > graph(cnNodeCount);

for(size_ti = 0;i < graph.size(); ++ i){

graph[i].resize(cnNodeCount,numeric_limits::max());

}

graph[0][1] = 5;

graph[0][2] = 1;

graph[0][3] = 2;

graph[0][4] = 3;

graph[1][0] = 5;

graph[1][2] = 4;

graph[1][3] = 2;

graph[1][4] = 2;

graph[2][1] = 4;

graph[2][0] = 1;

graph[2][3] = 5;

graph[2][4] = 3;

graph[3][1] = 2;

graph[3][2] = 5;

graph[3][0] = 2;

graph[3][4] = 2;

graph[4][1] = 2;

graph[4][2] = 3;

graph[4][3] = 2;

graph[4][0] = 3;

AA_TSP aa(graph);

aa.Get_AA_Path();

return0;

}

2 一般的旅行售货员问题

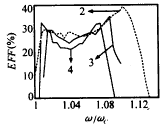
在费用函数不一定满足三角不等式的一般情况下，不存在具有常数性能比的解TSP问题的多项式时间近似算法，除非P=NP。换句话说，若P≠NP，则对任意常数ρ>1，不存在性能比为ρ的解旅行售货员问题的多项式时间近似算法。