在OPencv中采用的是Bouguet的极线校正的算法

在双目视觉中，我们对相机进行标定和校正，最终目的是使得两个相机的光轴完全平行，这样才能够继续后续的深度计算，三维重建。这样的校正在OPencv中采用的是Bouguet的极线校正的算法。

校正前的左右相机的光心并不是平行的，两个光心的连线就叫基线(主镜头中心的连线)，像平面与基线的交点就是极点，像点与极点所在的直线就是极线，左右极线与基线构成的平面就是空间点对应的极平面。

校正后，极点在无穷远处，两个相机的光轴平行。像点在左右图像上的高度一致。这也就是极线校正的目标。校正后做后续的立体匹配时，只需在同一行上搜索左右像平面的匹配点即可，能使效率大大提高。

Bouguet的方法是一种标定立体矫正方法,需要实现对左右相机进行标定，是将OPencv求解出来的旋转和平移矩阵分解成左右相机各旋转一半的旋转和平移矩阵R1,T1与R2,T2。分解的原则是使得，左右图像重投影造成的畸变最小，左右视图的共同面积最大。

1、将右图像平面相对于左图像平面的旋转矩阵分解成两个矩阵Rl和Rr，叫做左右相机的合成旋转矩阵。将左右相机各旋转一半，使得左右相机的光轴平行。此时左右相机的成像面达到平行，但是基线与成像平面不平行(行不对准)。

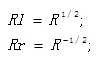
此时两个矩阵满足以下关系,通过这个关系可以看出来rl和rr是正交阵

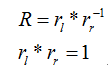
2、构造变换矩阵Rrect使得基线与成像平面平行(行对准)。构造的方法是通过右相机相对于左相机的偏移矩阵T完成的。

(1) 首先先创建一个由极点el方向开始的旋转矩阵,令主点(cx,cy)为左图像原点,则极点el的方向就是相机投影中心之间的平移向量方向.

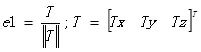
(2) e2方向与主光轴方向正交，沿图像方向，与e1垂直，则知e2方向可通过e1与主光轴方向的叉积并归一化获得。

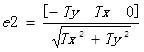
(3) 获取了e1与e2后，e3与e1和e2正交，e3自然就是他们两个的叉积：

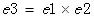
Rrect如下：

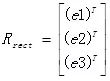
(4) 通过合成旋转矩阵与变换矩阵相乘获得左右相机的整体旋转矩阵。左右相机坐标系乘以各自的整体旋转矩阵就可使得左右相机的主光轴平行，且像平面与基线平行。

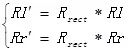
3. 通过上述的两个整体旋转矩阵，就能够得到理想的平行配置的双目立体系图像。校正后根据需要对图像进行裁剪，需重新选择一个图像中心，和图像边缘从而让左、右叠加部分最大。