编者按:在机器学习面前,我们都像一个孩子。当刚学会反向传播算法时,许多人会不满足于最基础的感知器,去尝试搭建更深、层数更多的神经网络。他们欣赏着自己的实现,就像沙滩上的孩子骄傲地看着自己用泥沙堆起来的城堡。但和城堡的徒有其表一样,这些神经网络的性能往往也难以令人满意,它们也许会陷入无休止的训练,也许准确率永远提不上来。这时,一些人就会开始怀疑:难道神经网络不是最先进的技术?
类似的怀疑,谁都有过——
神经网络的训练过程包括前向传播和反向传播两个部分,如果前向传播得到的预测结果和实际结果不符,这就说明网络没有训练好,要用反向传播去重新调整各个权重。这之中涉及各种常见的优化算法,以梯度下降为例,它的思路是把当前梯度的负值方向作为搜索方向,通过调整权重使目标函数趋近局部最小值,也就是让代价函数/损失函数越来越小。
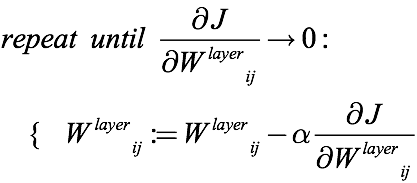
如上式所述,梯度下降算法用原权重减去乘上标量α(0到1之间)的梯度来更新权重,并“重复”这一过程直至收敛。但在实际操作中,这个“重复”的迭代次数是一个人为选定的超参数,这意味着它可能过小,最后收敛效果并不好;它也可能过大,网络被训练得“没完没了”。因此训练时间和训练效果之间存在“过犹不及”的尴尬情况。
那么这个超参数是怎么影响收敛的?就像不同人下山速度不同一样,梯度下降有一个下降步长,迭代时间越短,步长就越大,虽然收敛速度很快,但它容易无法精确收敛到最后的最优解;相反地,如果迭代时间过长,步长越小,那在很长一段收敛过程中,可能网络的权重并不会发生太大改变,而且相对大步长,小步长在规定迭代次数内接近最小值也更难。

小步长收敛宛如“蜗牛”
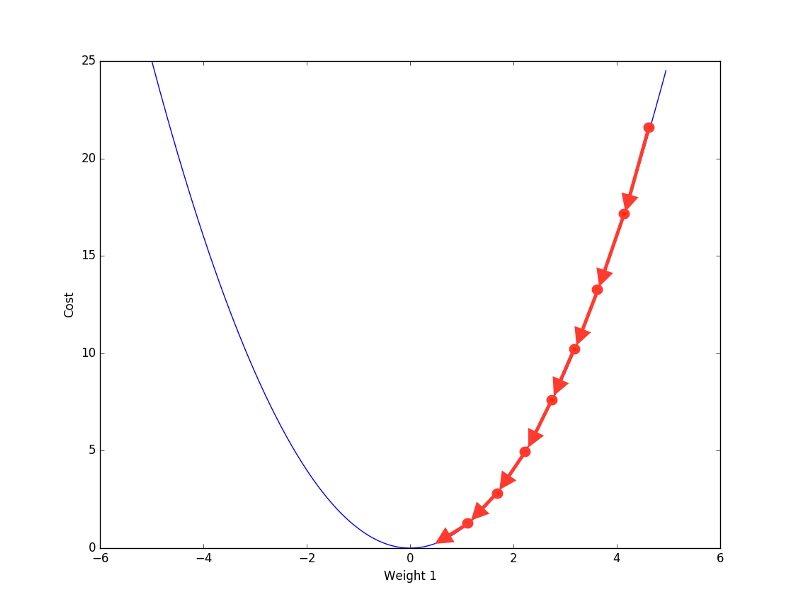
大步长收敛效率更高
这还不是唯一的毛病,当梯度数值过小时,它容易被四舍五入为0,也就是下溢出。这时再对这个数做某些运算就会出问题。
看到这里,我们似乎已经得到这样一个事实:小梯度 = 不好。虽然这个结论看起来有些武断,但在很多情况下,它并不是危言耸听,因为本文要讲的梯度消失就是由小梯度引起的。
让我们回想一下sigmoid函数,这是一个经常会在分类问题中遇到的激活函数:
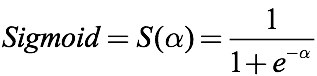
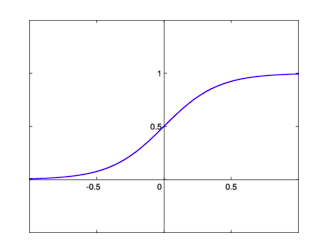
如上图所示,sigmoid的作用确实是有目共睹的,它能把任何输入的阈值都限定在0到1之间,非常适合概率预测和分类预测。但这几年sigmoid与tanh却一直火不起来,凡是提及激活函数,大家第一个想到的就是ReLU,为什么?
因为sigmoid几乎就是梯度消失的代名词,我们先对它求导:
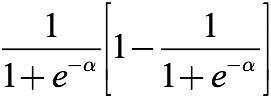
这看起来就是个很普通的 s(1-s) 算式,好像没什么问题。让我们绘制它的图像:
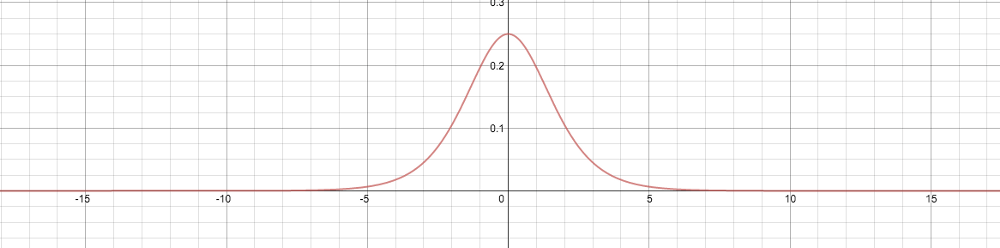
仔细看一看,还是没问题吗?可以发现,上图中最大值只有1/4,最小值无限接近0,换言之,这个导数的阈值是(0, 1/4]。记住这个值,待会儿我们会用到。
现在我们先回头继续讨论神经网络的反向传播算法,看看梯度对它们会产生什么影响。

这是一个最简单的神经网络,除了输入神经元,其他神经元的act()都来自前一层的神经元:先用act()乘上一个权重,再经激活函数馈送进下一层,来自上层的信息就成了一个全新的act()。最后的J归纳了前馈过程中的所有误差项(error),输出网络整体误差。这之后,我们再执行反向传播,通过梯度下降修改参数,使J的输出最小化。
下面是第一项权重w1的导数:

我们可以利用权重的导数来进行梯度下降,继而迭代出全局最优点,但在那之前,这个派生的乘法运算值得关注:
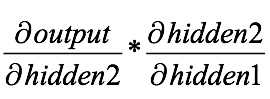
由于上一层的输出乘上激活函数就是下一层的输入,所以上式其实还包含sigmoid的导数,如果把信息全部表示完整,从输出返回到第二层隐藏层的表达式应该是:
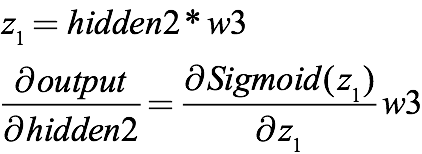
同理,从第二层隐藏层到第一层隐藏层则是:
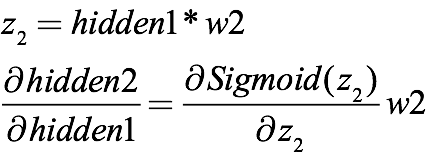
它们都包含sigmoid函数,合起来就是:
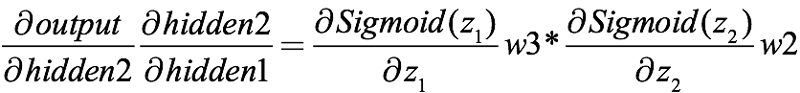
之前我们已经对sigmoid求过导了,计算出它的阈值是(0, 1/4]。结合上式,两个0到1之间的小数相乘,积小于任一乘数。而在典型的神经网络中,权重初始化的一般方法是权重的选择要服从均值=0,方差=1的正态分布,因此这些初始权重的阈值是[-1, 1]。
接下来的事情就很清楚了:
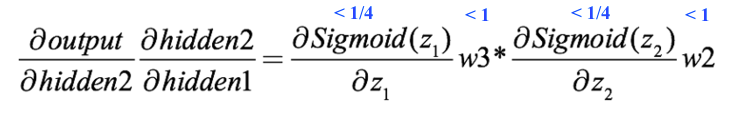
即便不用常规权重初始化方法,w2和w3大于1,但它们对两个sigmoid导数相乘来说还是杯水车薪,梯度变得太小了。而在实际操作中,随机权重是很可能小于1的,所以那时它反而是在助纣为虐。
这还只有2个隐藏层,试想一下,如果这是一个工业级的深层神经网络,那么当它在执行反向传播时,这个梯度会变得有多小,小到突然消失也在情理之中。另一方面,如果我们把然激活函数导数的绝对值控制在大于1,那这个连乘操作也很吓人,结果会无限大,也就是我们常说的“梯度爆炸”。
现在,我们来看一个典型的ANN:
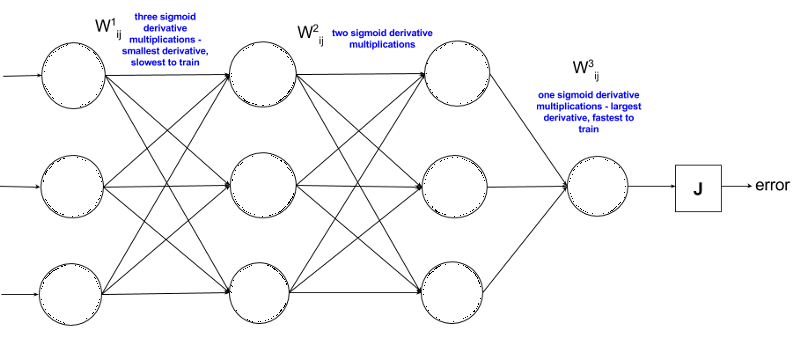
第一项权重距离误差项J最远,因此求导后它的表达式最长,也包含更多sigmoid函数,计算结果更小。所以神经网络的第一层往往是训练时间最长的一层。它同时也是后面所有层的基础,如果这一层不够准确,那就会产生连锁反应,直接拉低整个网络的性能。
这就也是神经网络,尤其是深层神经网络一开始并不为行业所接受的原因。正确训练前几层是整个网络的基础,但激活函数的缺陷和硬件设备的算力不足,使当时的研究人员连打好基础都做不到。
看到这里,我们应该都已经理解sigmoid函数的缺点了,它的替代方案tanh函数虽然也曾声名大噪,但考虑到tanh(x)=2sigmoid(2x)-1,它肯定也存在同样的问题。那么,现在大家都在用的ReLU好在哪儿?
首先,ReLU是一个分段函数:
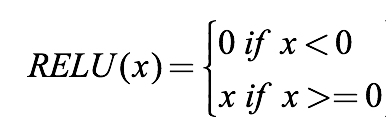
它还有另一种写法:
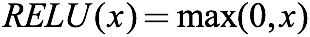
当输入小于0时,函数输出0;当输入大于零时,函数输出x。
我们计算它的导数来对比sigmoid:
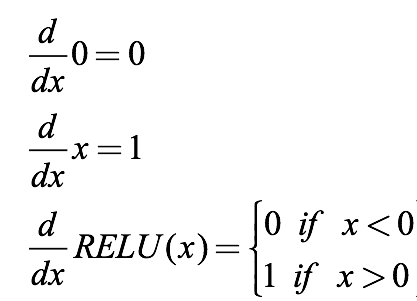
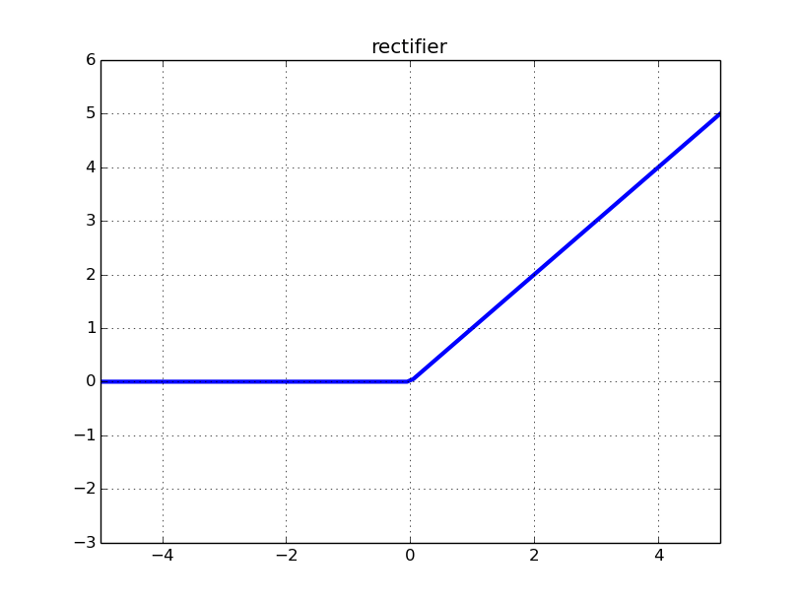
然后是它的图像,注意一点,它在0点不可微,所以当x=0时,图中y轴上应该是两个空心圆。
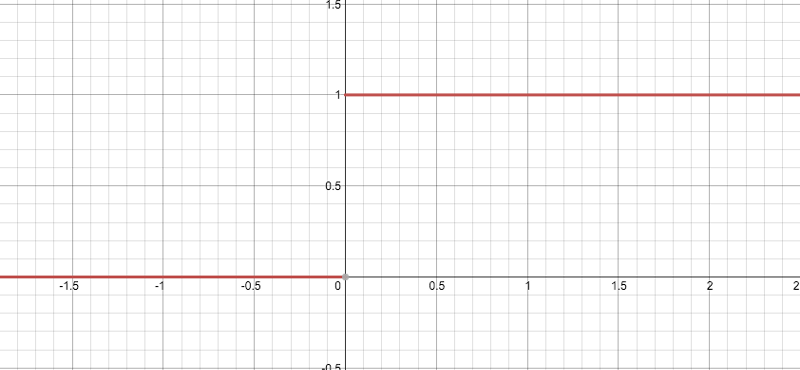
可以发现,导数的阈值终于不再是(0, 1)了,它好像可以避免梯度消失,但似乎又有点不对劲?当我们把一个负值输入到ReLU函数后,梯度为0,这时这个神经元就“坏死”了。换句话说,如果存在负数权重,那某些神经元可能永远不会被激活,导致相应参数永远不会被更新。从某种意义上来说,ReLU还是存在部分梯度消失问题。
那么,我们该怎么选择呢?不急,这里还有一种激活函数——Leakly ReLU。
既然ReLU的“梯度消失”源于它的阈值0,那么我们可以把它重设成一个0到1之间的具体小数。这之后,当输入为负时,它还是具有非常小的梯度,这就为网络继续学习提供了机会。
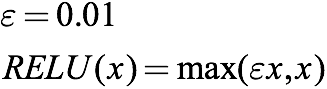
上式中的ε=0.01,但它最常见的范围是0.2-0.3。因为斜率小,输入负值权重后,它在图像上是一条非常缓的线:
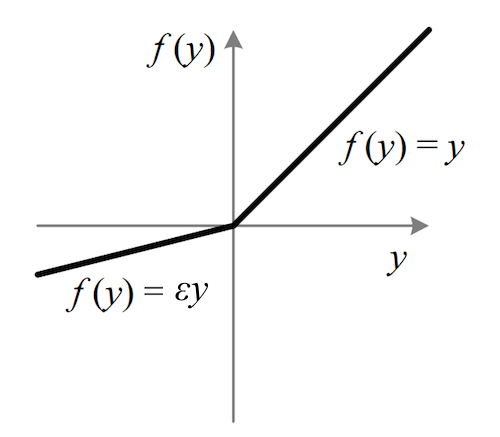
这里我们要声明一点:虽然Leakly ReLU可以解决ReLU的神经元坏死问题,但它的表现并不一定比ReLU更好。比如常数ε万一过小,它就很可能会导致新的梯度消失。另一方面,这两个激活函数有个共同的缺点,即不像tanh和sigmoid一样输出有界,如果是在RNN这样很深的神经网络里,即便ReLU的导数是0或1,很小,但除了它我们还有那么多权重,多项连乘会导致非常大的输出值,然后梯度就爆炸了。
所以总的来说,ReLU并没有根治梯度消失这个问题,它只是在一定程度上缓解了矛盾,并产生了另一个新问题。这也是这些激活函数至今还能共存的原因——CNN用ReLU更常见,而RNN大多用tanh。在“玄学”的大背景下,这大概是新手入门机器学习后,接触到的第一起trade off吧。
-
神经网络
+关注
关注
42文章
4774浏览量
100891 -
梯度
+关注
关注
0文章
30浏览量
10331 -
深度学习
+关注
关注
73文章
5507浏览量
121272
原文标题:深度学习解密:我的梯度怎么消失了?
文章出处:【微信号:jqr_AI,微信公众号:论智】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
详解深度学习、神经网络与卷积神经网络的应用





 一些人会怀疑:难道神经网络不是最先进的技术?
一些人会怀疑:难道神经网络不是最先进的技术?

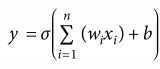










评论