MIT CSAIL的研究人员发现,隐藏层仅有一个神经元的ResNet就是一个通用的函数逼近器,恒等映射确实加强了深度网络的表达能力。研究人员表示,这一发现还填补了全连接网络表达能力强大原因的理论空白。
深度神经网络是当前很多机器学习应用成功的关键,而深度学习的一大趋势,就是神经网络越来越深:以计算机视觉应用为例,从最开始的AlexNet,到后来的VGG-Net,再到最近的ResNet,网络的性能确实随着层数的增多而提升。
研究人员的一个直观感受是,随着网络深度的增大,网络的容量也变高,更容易去逼近某个函数。
因此,从理论方面,也有越来越多的人开始关心,是不是所有的函数都能够用一个足够大的神经网络去逼近?
在一篇最新上传Arxiv的论文里,MIT CSAIL的两位研究人员从ResNet结构入手,论证了这个问题。他们发现,在每个隐藏层中只有一个神经元的ResNet,就是一个通用逼近函数,无论整个网络的深度有多少,哪怕趋于无穷大,这一点都成立。
一个神经元就够了,这不是很令人兴奋吗?
从深度上理解通用逼近定理
关于神经网络的表达能力(representational power)此前已经有很多讨论。
上世纪80年代的一些研究发现,只要有足够多的隐藏层神经元,拥有单个隐藏层的神经网络能以任意精度逼近任意连续函数。这也被称为通用逼近定理(universal approximation theorem)。
但是,这是从“宽度”而非“深度”的角度去理解——不断增加隐藏层神经元,增加的是网络的宽度——而实际经验告诉我们,深度网络才是最适用于去学习能解决现实世界问题的函数的。
因此,这就自然引出了一个问题:
如果每层的神经元数量固定,当网络深度增加到无穷大的时候,通用逼近定理还成立吗?
北京大学Zhou Lu等人发表在NIPS 2017的文章《The Expressive Power of Neural Networks: A View from the Width》发现,对于用ReLU作为激活函数的全连接神经网络,当每个隐藏层至少有 d+4 个神经元(d表示输入空间)时,通用逼近定理就成立,但至多有 d 个神经元时,就不成立。
那么,换一种结构,这个条件还会成立吗?究竟是什么在影响深度网络的表达能力?
MIT CSAIL的这两位研究人员便想到了ResNet。
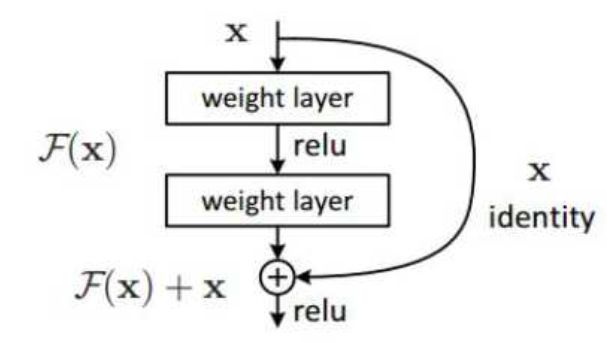
从何恺明等人2015年提出以来,ResNet甚至被认为是当前性能最佳的网络结构。ResNet的成功得益于它引入了快捷连接(shortcut connection),以及在此基础上的恒等映射(Identity Mapping),使数据流可以跨层流动。原问题就转化使残差函数(F(x)=H(x)-x)逼近0值,而不用直接去拟合一个恒等函数 H’(x)。
由于恒等映射,ResNet的宽度与输入空间相等。因此,作者构建了这样的结构,并不断缩小隐藏层,看看极限在哪里:
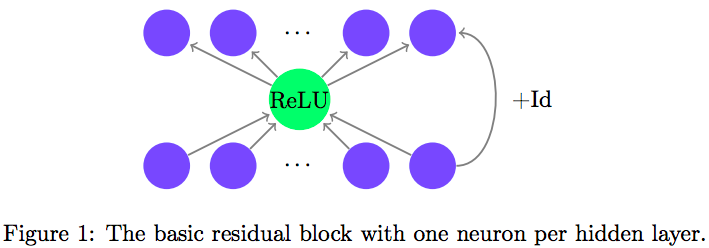
结果就如上文所说的那样,最少只需要一个神经元就够了。
作者表示,这进一步从理论上表明,ResNet的恒等映射确实增强了深度网络的表达能力。

例证:完全连接网络和ResNet之间的区别
作者给出了一个这样的toy example:我们首先通过一个简单的例子,通过实证探索一个完全连接网络和ResNet之间的区别,其中完全连接网络的每个隐藏层有 d 个神经元。例子是:在平面中对单位球(unit ball)进行分类。
训练集由随机生成的样本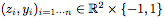 组成,其中
组成,其中
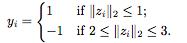
我们人为地在正样本和负样本之间创建了一个边界,以使分类任务更容易。我们用逻辑损失作为损失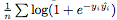 ,其中
,其中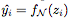 是网络在第 i 个样本的输出。在训练结束后,我们描绘了各种深度的网络学习的决策边界。理想情况下,我们希望模型的决策边界接近真实分布。
是网络在第 i 个样本的输出。在训练结束后,我们描绘了各种深度的网络学习的决策边界。理想情况下,我们希望模型的决策边界接近真实分布。
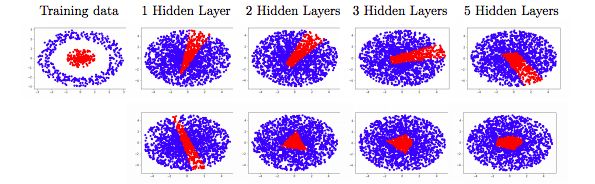
图2:在单位球分类问题中,训练每个隐藏层(上面一行)宽度 d = 2 的全连接网络和每个隐藏层只有一个神经元的 ResNet(下面一行)得到的决策边界。全连接网络无法捕获真正的函数,这与认为宽度 d 对于通用逼近而言太窄(narrow)的理论是一致的。相反,ResNet很好地逼近了函数,支持了我们的理论结果。
图2显示了结果。对于完全连接网络(上面一行)而言,学习的决策边界对不同的深度具有大致相同的形状:逼近质量似乎没有随着深度增加而提高。虽然人们可能倾向于认为这是由局部最优性引起的,但我们的结果与文献[19]中的结果一致:
Proposition 2.1. 令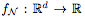 为由一个具有ReLU激活的完全连接网络 N 定义的函数。用
为由一个具有ReLU激活的完全连接网络 N 定义的函数。用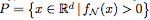 表示
表示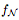 的正水平集。如果 N 的每个隐藏层至多有 d 个神经元,那么
的正水平集。如果 N 的每个隐藏层至多有 d 个神经元,那么
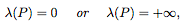 , 其中 λ 表示 Lebesgue measure
, 其中 λ 表示 Lebesgue measure
换句话说,“narrow”的完全连接网络的水平集(level set)是无界的,或具有零测度。
因此,即使当深度趋于无穷大时,“narrow”的完全连接网络也不能逼近有界区域。这里我们只展示了 d=2 的情况,因为可以很容易地看到数据;在更高的维度也可以看到同样的观察结果。
ResNet的决策边界看起来明显不同:尽管宽度更窄,但ResNet表示了一个有界区域的指标。随着深度的增加,决策边界似乎趋于单位球,这意味着命题2.1不能适用于ResNet。这些观察激发了通用逼近定理。
讨论
在本文中,我们展示了每个隐藏层只有一个神经元的ResNet结构的通用逼近定理。这个结果与最近在全连接网络上的结果形成对比,对于这些全连接网络,在宽度为 d 或更小时,通用逼近会失败。
ResNet vs 全连接网络:
虽然我们在每个基本残差块(residual block)中只使用一个隐藏神经元来实现通用逼近,但有人可能会说,ResNet的结构仍然将identity传递到下一层。这个identity map可以算作 d 个隐藏单元,导致每个残差块共有 d+1 个隐藏单元,并且使得网络被看做一个宽度为 (d + 1)的完全连接网络。但是,即使从这个角度看,ResNet也相当于一个完全连接网络的压缩或稀疏版本。特别是,宽度为 (d + 1)的完全连接网络每层具有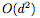 个连接,而ResNet中只有
个连接,而ResNet中只有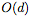 个连接,这要归功于identity map。完全连接网络的这种“过度参数化”或许可以解释为什么dropout对这类网络有用。
个连接,这要归功于identity map。完全连接网络的这种“过度参数化”或许可以解释为什么dropout对这类网络有用。
同样的道理,我们的结果表明宽度(d + 1)的完全连接网络是通用逼近器,这是新的发现。文献[19]中的结构要求每层d + 4个单元,在上下边界之间留有空隙。因此,我们的结果缩小了差距:宽度为(d + 1)的完全连接网络是通用逼近器,而宽度为d的完全连接网络不是。
为什么通用逼近很重要?如我们在论文第2节所述,宽度为d的完全连接网络永远不可能逼近一个紧凑的决策边界,即使我们允许有无限的深度。然而,在高维空间中,很难对得到的决策边界进行可视化和检查。通用逼近定理提供了一种完整性检查,并确保原则上我们能够捕获任何期望的决策边界。
训练效率:
通用逼近定理只保证了逼近任何期望函数的可能性,但它并不能保证我们通过运行SGD或任何其他优化算法能够实际找到它。理解训练效率可能需要更好地理解优化场景,这是最近受到关注的一个话题。
这里,我们试图提出一个稍微不同的角度。根据我们的理论,带有单个神经元隐藏层(one-neuron hidden layers)的ResNet已经是一个通用的逼近器。换句话说,每一层有多个单元的ResNet在某种意义上是模型的过度参数化,而过度参数化已经被观察到有利于优化。这可能就是为什么训练一个非常深的ResNet比训练一个完全连接的网络“更容易”的原因之一。未来的工作可以更严谨地分析这一点。
泛化:
由于一个通用逼近器可以拟合任何函数,人们可能会认为它很容易过度拟合。然而,通常可以观察到,深度网络在测试集上的泛化效果非常出色。对这一现象的解释与我们的论文是不相关的,但是,了解通用逼近能力是这一理论的重要组成部分。此外,我们的结果暗示了,前述的“过度参数化”也可能发挥作用。
总结:
总结而言,我们给出了具有单个神经元隐藏层的ResNet的通用逼近定理。这从理论上将ResNet和完全连接网络区分开来,并且,我们的结果填补了理解完全连接网络的表示能力方面的空白。在一定程度上,我们的结果在理论上激励了对ResNet架构进行更深入的实践。
-
神经网络
+关注
关注
42文章
4772浏览量
100803 -
神经元
+关注
关注
1文章
363浏览量
18458 -
深度学习
+关注
关注
73文章
5503浏览量
121200
原文标题:【一个神经元统治一切】ResNet 强大的理论证明
文章出处:【微信号:AI_era,微信公众号:新智元】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐




 一个神经元的ResNet就是一个通用的函数逼近器
一个神经元的ResNet就是一个通用的函数逼近器










评论