现有GAN存在哪些关键属性缺失？

近日，加拿大犹太综合医院Lady Davis Institute的生物统计学家Alexia Jolicoeur-Martineau发表了一篇令人瞩目的论文，引起“GAN之父”Ian Goodfellow的注意。在论文中，她指出现有的标准GAN（SGAN）还缺少一个基本属性，即训练生成器时，我们不仅应该提高伪数据是真实数据的概率，还应该降低实际数据是真实数据的概率。这个属性是一个重要基础，它也是所有GAN都应该遵守的。

在标准生成对抗网络（SGAN）中，判别器负责估计输入数据是真实数据的概率，根据这个数值，我们再训练生成器以提高伪数据是真实数据的概率。但本文认为，判别器在提高“伪数据为真”的概率的同时，也应该降低“实际数据为真”的概率，原因有三：

mini-batch中一半的数据是伪数据，这个先验会带来不合逻辑的结果；

在最小化散度（divergence minimization）的过程中，两个概率不是同步变化；

实验证实，经过相对判别器诱导，SGAN的性能可以媲美基于IPM的GAN（WGAN、WGAN-GP等），而后者实际上已经具有相对判别器的雏形，因此也更稳定。

本文提出相对GAN（RGAN），并在它的基础上又提出了一个变体——相对均值GAN（RaGAN），变体用平均估计计算判别器概率。此外，论文还显示基于IPM的GAN其实是RGAN的子集。

通过比较，文章发现：(1)相比非相对GAN，RGAN和RaGAN更稳定，产出的数据样本质量更高；(2)在RaGAN上加入梯度惩罚后，它能生成比WGAN-GP质量更高的数据，同时训练时长仅为原先的1/5；(3)RaGAN能够基于非常小的样本（N = 2011）生成合理的高分辨率图像（256x256），撇开做不到的GAN和LSGAN，这些图像在质量上也明显优于WGAN-GP和SGAN生成的归一化图像。

背景简介

GAN是Ian Goodfellow等人在2014年提出的新型神经网络，它一经面世就收获大量关注，并在学界持续发酵。本文把最原始的GAN称为标准GAN，也就是SGAN，它由一个生成器G和一个判别器D构成，前者负责生成伪图像，后者负责评估这个伪图像是真实图像的概率，然后输出结果帮助生成器继续训练，直到最后生成判别器都难辨真假的伪图。

从计算角度看，GAN的生成器和判别器如下所示。其中f1,f2, g1, g2都是输入标量-输出标量的函数，P表示真实数据分布（xr实际数据），Q表示伪数据分布（xf伪数据），Pz是以0为中心的多元正态分布，方差为1，D(x)是判别器在x出的评估值。

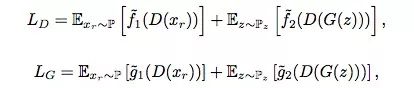
一般形式

独立形式：谷歌论文Are GANs Created Equal?

对于生成器，SGAN提出了两种损失函数：saturating和non-saturating。其中前者不稳定，后者较稳定。如果GAN能100%分类真伪数据，那saturating函数的梯度是0，non-saturating的梯度虽然不为0，但它是易变的（volatile）。这意味着如果学习率过高，判别器很可能会“放弃”学习，导致模型性能很差，这种现象在高维数据中尤为明显。

虽然近几年许多研究人员提出了很多新的损失函数，但它们相比SGAN没有太多根本上的进展，因此大多数GAN可以用non-saturating和saturating函数简单地分成两类：g1=− f1and g2=− f2，saturating；g1=f1and g2=f2，non-saturating。从本质上来说，它们有一定的相通之处，为了后面方便对比，本文假设所有GAN都用non-saturating损失函数。

另外，一些研究人员发现把IPM（Integral probability metrics积分概率指标）用于GAN可以大幅提高最终结果，但至于IPM为什么能得到这样的效果，他们并没有给出说明。而根据本文的研究，IPM GAN背后起作用的正是相对判别器。

SGAN遗漏的关键元素

本文论证的过程分为两块，一是直接分析“降低实际图像是真实图像概率”的必要性，二是用提出的RGAN和RaGAN和上述GAN做对比。本章是第一部分。

先验知识

这块内容比较简单。经过足够训练后，判别器如果性能过关，那它就应该能正确区分大多数图像的真伪性，把实际图像归类为真实图像，把伪图像归类为非真实图像。而生成器的目标是“愚弄”判别器，让后者把更多的伪图像分类为真实图像，所以它会把一半实际图像和一半伪图像输入判别器，期待从中学到更多真实图像的分布。

虽然听起来很有道理，但这是不合逻辑的。如果实际数据和伪数据看起来差不多，那大多数图像的评估都符合C(xf) ≈ C(xr)。这时，如果判别器事先知道输入图像中一半真一半假，那它会认为每张图像为真的概率是0.5；如果判别器事先不知道，那它很可能就直接输出D(x) ≈ 1。

如果生成器的学习率设得很高/迭代次数很多，再加上判别器输出了个约等于1的概率，这时生成器“眼里”的实际数据和伪数据是不平等的，它会认为伪数据更真实，C(xf) > C(xr)。而如果是坚信有一半伪数据的判别器，它会被迫把实际图像分类成伪数据，背离正确分类的目标。

最小化散度

在SGAN中，我们认为判别器损失函数等于Jensen-Shannon散度（JSD）。因此，计算JSD可以等同为计算这个式子的最大值：

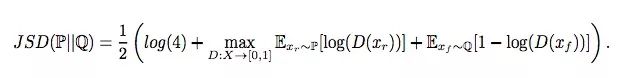
对于xr∈P和xf∈Q，如果D(xr) = D(xf) = 0.5，JSD最小化；如果D(xr) = 1，D(xf) = 0，JSD最大化。

如果我们想在JSD的最大值和最小值之间得出一个最小化的散度，这相当于D(xr)的阈值是(0.5, 1)，D(xf)的阈值是(0, 0.5)。但如下图所示，当我们执行最小化时，变化的只有D(xf)，而对实际图像计算出的概率D(xr)却没有发生改变，这不合理。

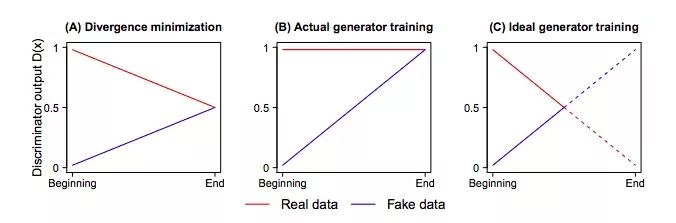
梯度

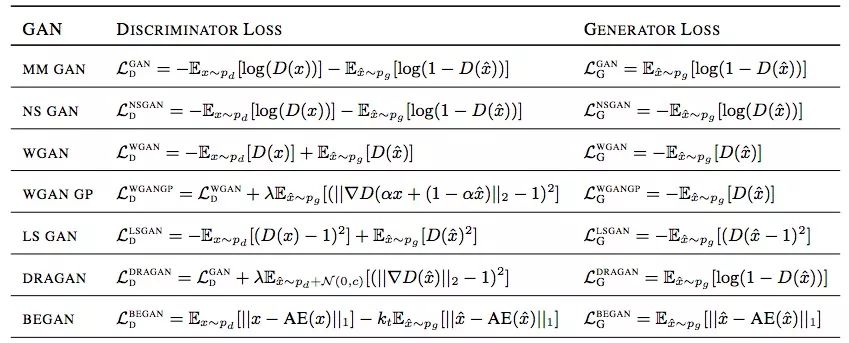
下面是SGAN和IPM GAN的损失函数对比：

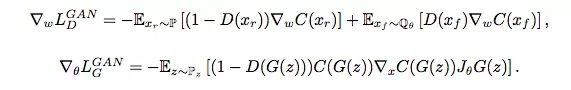
SGAN

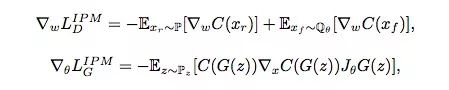
基于IPM的GAN

从这几个方程可以看出，当同时满足以下几点时，SGAN和 IPM GAN的结果是差不多的：

SGAN的判别器：D(xr) = 0，D(xf) = 1；

SGAN的生成器：D(xf) = 0；

C(x)∈F。

换句话说，如果生成器能直接影响判别器，那SGAN和基于IPM的GAN可以性能相近。对于后者，GAN在计算判别器损失函数梯度时会同时考虑实际数据和伪数据，但SGAN的D(xr)是不会随着D(xf)变化而变化的，它会停止学习，转而更关注伪数据。另一方面，如果D(xr)会随D(xf)的上升而下降，这就意味着真实数据会被纳入梯度计算中，这也是基于IPM的GAN更稳定，而SGAN更容易崩溃的原因。

实验对比

简而言之，相对的GAN和普通GAN的区别如下所示。

标准GAN（SGAN）的判别器：

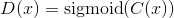
相对标准GAN（RSGAN）的判别器：

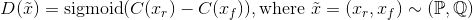
相对均值标准GAN（RaSGAN）的判别器：

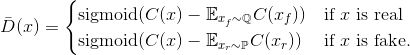
翻译后的论文图

CIFAR-10上的FID值对比，RSGAN表现出众

在LSGAN中引入相对判别器后生成的128×128猫图，FID值仅为15.85

WGAN-GP生成的256×256猫图，FID>100