编者按:如下图所示,这是一个非常基础的分类问题:空间中存在两个高维聚类(两簇蓝点),它们被一个超平面分离(橙线)。其中两个白色圆点表示两个聚类的质心,它们到超平面的欧氏距离决定了模型的性能,而橙色虚线正是它们垂直的方向。
在这类线性分类问题中,通过调整L2正则化的水平,我们能不断调整这个垂直方向的角度。但是,你能解释这是为什么吗?

许多研究已经证实,深层神经网络容易受对抗样本影响。通过在图像中加入一些细微扰动,分类模型会突然脸盲,开始指猫为狗、指男为女。如下图所示,这是一个美国演员人脸分类器,输入一张正常的Steve Carell图像后,模型认为照片是他本人的概率有0.95。但当我们往他脸上稍微加了点料,他在模型眼里就成了女演员Zooey Deschanel。
这样的结果令人忧心。首先,它挑战了一个基础共识,即新数据的良好泛化和模型对小扰动的稳健性(鲁棒性)是相互促进的,上图让这个说法站不住脚。其次,它会对现实应用构成潜在威胁,去年11月,MIT的研究人员曾把扰动添加到3D物品上,成功让模型把海龟分类成枪支。鉴于这两个原因,理解这种现象并提高神经网络的稳健性已经成为学界的一个重要研究目标。
近年来,一些研究人员已经探索了几种方法,比如描述现象、提供理论分析和设计更强大的架构,对抗训练现在也已经成了新的正则化技术。不幸的是,它们都没能从根本上解决这个问题。面对这一困难,一种可行的思路是从最基础的线性分类出发,去逐步分解问题的复杂度。
玩具问题
在线性分类问题中,我们一般认为对抗性扰动就是高维空间中的点积。对此,一种非常普遍的说法是:我们可以在高维问题中对输入进行大量无限小的改变,从而使输出发生巨变。但这种说法其实是有问题的。事实上,当分类边界靠近数据流形时,对抗样本依然存在——换句话说,它独立于图像空间维度。
建模
让我们从一个最小的玩具问题开始:一个二维图像空间,其中每个图像都是关于a和b的函数。
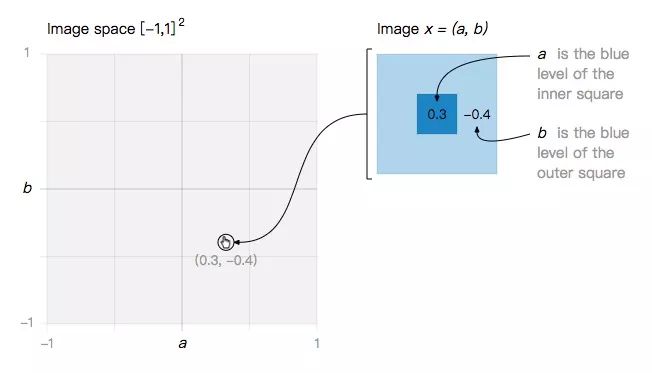
在这个简单的图像空间内,我们定义两类图像:

它们可以用无数个线性分类器进行分类,比如下图的Lθ:
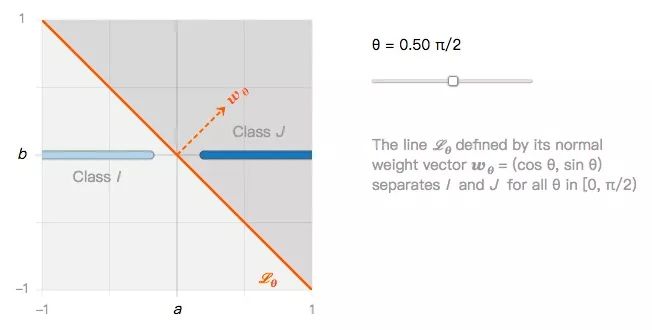
由此我们可以提出第一个问题:如果所有线性分类器都能很好地分类I类图像和J类图像,那它们是否也能同样稳健地分类图像扰动?
投影和镜像
假设x是I中的一张图像,它距离J类图像的最近距离是它到分类边界的投影,也就是x到Lθ的垂直距离:

当x和xp距离非常近时,我们把xp看做x的一个对抗样本。联系第一个问题,显然,xp被分类为I的置信度非常低,并不稳健。那么有没有置信度高的对抗样本呢?在下图中,我们根据之前的距离找到了x在J中的镜像图像xm:

不难理解,x和xm到分类边界的距离是一样的,它们的分类置信度也应该相同。
基于镜像构建关于θ的函数
让我们回到之前的玩具问题。有了图像x和它的镜像图像xm,我们可以据此构建一个包含θ的函数。
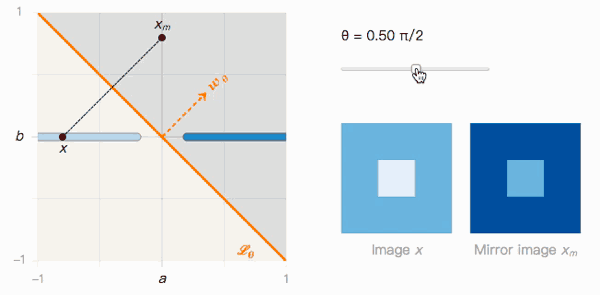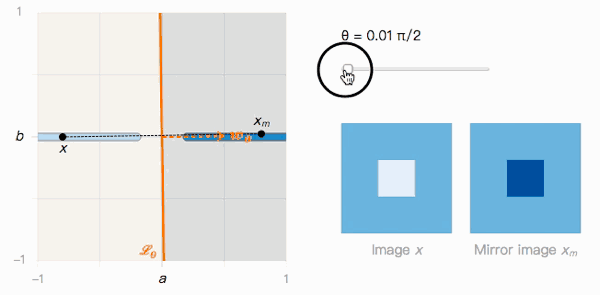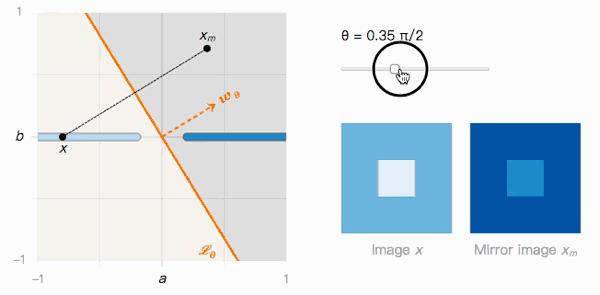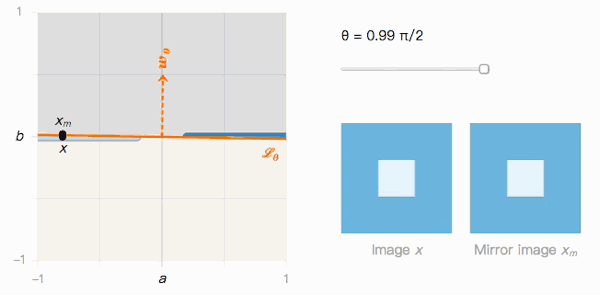
如上图所示,x到xm的距离取决于分类边界的夹角θ。我们来观察一下它的两个极值:

当θ=0时,Lθ没有受到对抗样本影响。x被分类为I的置信度很高,xm被分类为J的置信度也很高,我们可以轻松区分两者。
当θ→π/2时,Lθ很明显受到对抗样本影响。x被分类为I的置信度很高,xm被分类为J的置信度也很高,但它们在视觉上几乎不可区分。
这就带来了第二个问题:如果Lθ倾斜的越厉害,对抗样本存在的几率就越高,那事实上究竟是什么在影响Lθ?
过拟合和L2正则化
对于这个问题,本文的假设是标准线性模型,比如SVM、逻辑回归,是因为过拟合训练集中的噪声数据才导致过度倾斜的。Huan Xu等人在论文Robustness and Regularization of Support Vector Machines中的理论结果支持了这一假设,认为分类器的稳健性和正则化有一定关联。
要证明这一点不难,我们来做个实验:L2正则化是否可以削弱对抗样本的影响?
设训练集中存在一个噪声数据点p:
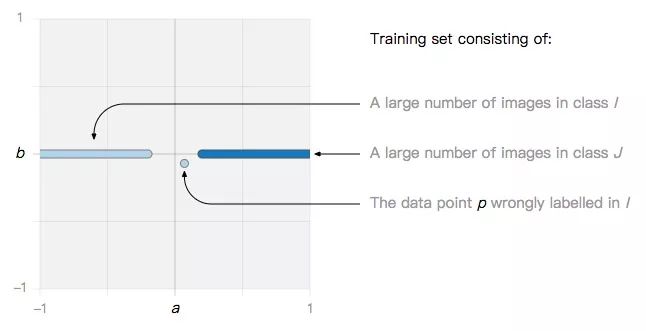
如果我们用的算法是SVM或逻辑回归,最后可能会观察到这两种情况。
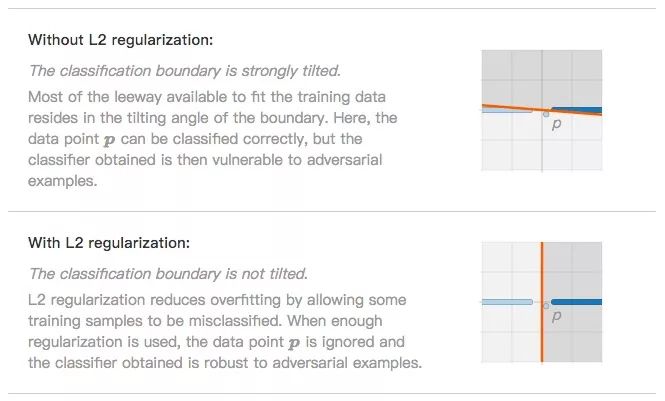
分类边界严重倾斜(无L2正则化)。为了尽量拟合数据点,分类边界会努力倾斜,让模型最终能准确分类p。这时分类器是过拟合的,也更易于受到对抗样本影响。
分类边界不倾斜(L2正则化)。L2正则化防止过拟合的思路是允许一小部分数据被分类错误,如噪声数据p。忽略它后,分类器在面对对抗样本时更稳健了。
看到这里,也许有人会有异议:上述数据是二维的,它和高维数据又有什么关系?
线性分类中的对抗样本
之前我们得出了两个结论:(1)分类边界越靠近数据流形,越容易出现对抗样本;(2)L2正则化可以控制边界的倾斜角度。虽然都是基于二维图像空间提出的,但对于一般情况,它们实际上都是成立的。
缩放损失函数
让我们从最简单的开始。L2正则化就是在损失函数后再加一个正则化项,不同于L1把权重往0靠,L2正则化的权重向量是不断下降的,因此它也被称为权重衰减。
建模
设I和J为高维图像空间Rd中的两类图像,C为线性分类器输出的超平面边界,它和权重向量w和偏置项b有关。x是Rd中的一幅图,则x到C的原始得分为:
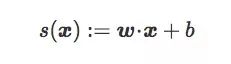
这个原始得分其实是x关于C的符号距离(signed distance,带正负号):
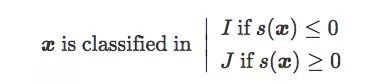
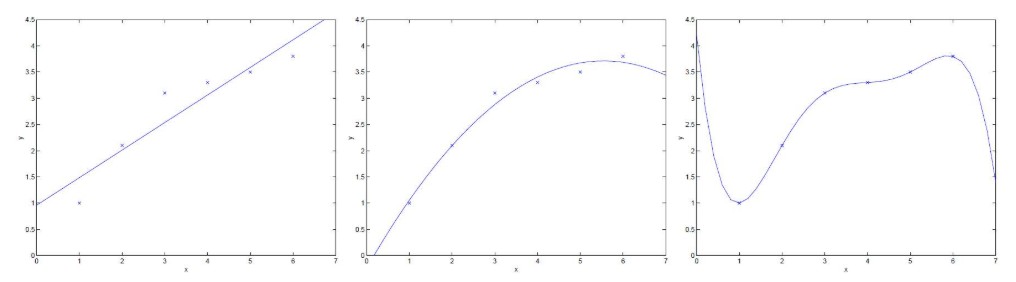
设存在一个包含n对(x,y)的训练集T,其中x是图像样本,当x∈I时,y=-1;当x∈J时,y=1。下面是T的三种分布:

分类器C的期望风险R(w,b),就是对训练集T的平均惩罚:
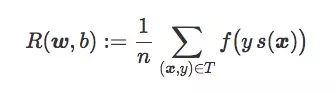
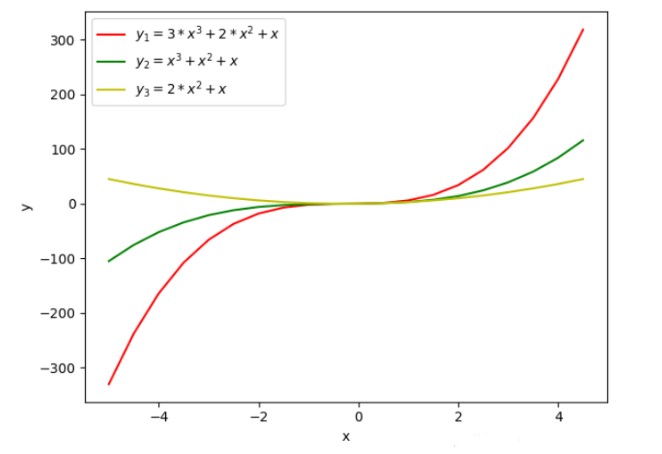
通常情况下,我们训练线性分类器时会用合适的损失函数f找到权重向量w和偏置项b,使R(w,b)最小。在一般二元分类问题中,下面是三个值得关注的损失函数:
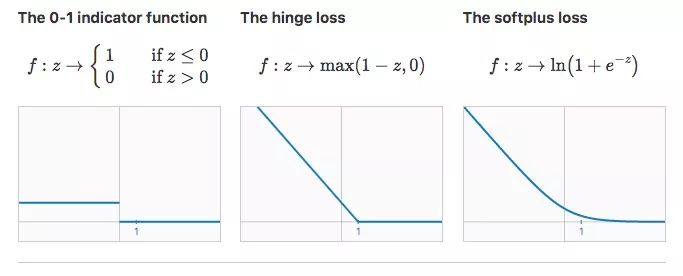
如上图所示,对于第一个损失函数,分类器的期望风险就是它的分类错误率。从某种意义上来说,这个损失函数是最理想的,因为我们只需最小化误差就能达成目标。但它的缺点是导数始终为0,我们不能在这个基础上用梯度下降。
事实上,上述问题现在已经被解决了,一些线性回归模型使用改进版损失函数,比如SVM的hinge loss和逻辑回归的softplus loss。它们不再继续在分类错误数据上使用固定惩罚项,而是用了一个严格递减的惩罚项。作为代价,这些损失函数也会给正确分类的数据带去副作用,但最终能保证找出一个较为准确的分类边界。
缩放参数‖w‖
之前介绍符号距离s(x)时,我们没有详细说明它的缩放参数w。如果d(x)是x到C的欧氏距离,我们有:
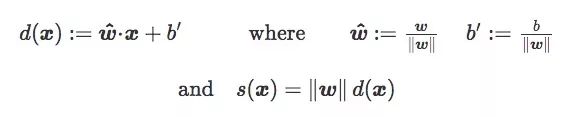
因此,‖w‖也可以被看作损失函数的缩放参数:

也就是:f‖w‖:z→f(‖w‖×z) 。
可以发现,这个缩放对之前提到的第一个损失函数没有影响,但对hinge loss和softplus loss却影响剧烈。

值得注意的是,对于缩放参数的极值,后两个损失函数变化一致。

更确切地说,两种损失函数都满足:
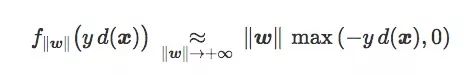
方便起见,我们将错误分类的数据定义为:

所以期望风险可以被改写成:

这个表达式包含了一个我们称之为“误差距离”的概念:

它是正的,可以解释为每个训练样本被C错误分类的平均距离(对正确分类数据的贡献为零)。它与训练误差有关,但不完全等同。
最后,我们可以得到:
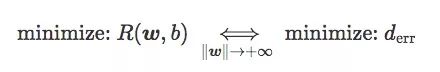
换句话说,当‖w‖足够大时,最小化hinge loss和softplus loss的期望风险就等于最小化误差距离,也就是最小化训练集上的错误率。
小结
综上所述,通过在损失函数后加上正则化项,我们能控制‖w‖的值,从而输出正则化的损失。

一个较小的正则化参数λ会让‖w‖失控增大,一个较大的λ会让‖w‖缩小。
总之,线性分类(SVM和逻辑回归)中使用的两个标准模型在两个目标之间取得平衡:它们在正则化参数低时最小化误差距离,并且在正则化系数高时最大化对抗距离。
对抗距离和倾斜角度
看到这里,我们又接触了一个新词——“对抗距离”——对抗性扰动的稳健性的度量。和之前二维图像空间的例子一样,它可以表示为包含单个参数的函数,这个参数即分类边界和最近的质心分类器之间的角度。
对于训练集T,如果我们按图像类别I和J把它分成TI和TJ,我们可以得到:
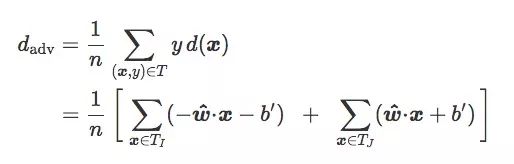
如果TI和TJ是均等的(n=2nI=2nJ):
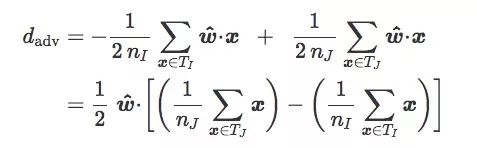
设TI和TJ的质心分别是i和j:

现在有一个离分类边界最近的质心分类器,它的法向量是z^=(j−i)/‖j−i‖:
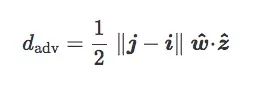
最后,我们将包含w^和z^的平面称为C的倾斜平面,我们称之为w^和z^之间的夹角θ为C的倾斜角度:

这个等式的几何含义如下图所示:

综合以上推算,在给定训练集T上,如果两个质心‖j−i‖之间的距离是个固定值,那对抗距离dadv仅取决于倾斜角θ。通俗地讲:
当θ=0时,对抗距离最大,对抗样本影响最小;
当θ→π/2时,对抗距离最小,对抗样本对分类器的影响最大。
最后的话
尽管对抗样本已经被研究了很多年,尽管它在理论和实践中都对机器学习领域具有重要意义,但学界对它的研究还非常有限,它对很多人来说还是个迷。这篇文章给出了线性模型下对抗样本的生成情况,希望能给对这方面感兴趣的新人提供一定见解。
可惜的是,现实并没有文章描述的这么简单,随着数据集变大、神经网络不断加深,对抗样本也正变得越来越复杂。根据我们的经验,模型包含的非线性因素越多,权重衰减似乎就越有用。这个发现可能只是浅层次的,但更深层次的内容将交给不断涌现的新人来解决。可以肯定的一点是,如果要对这个困难给出一个令人信服的解决方案,我们需要在深度学习中见证一种新的革命性观念的诞生。
-
神经网络
+关注
关注
42文章
4760浏览量
100480 -
图像
+关注
关注
2文章
1082浏览量
40396 -
分类器
+关注
关注
0文章
152浏览量
13169
原文标题:L2正则化视角下的对抗样本
文章出处:【微信号:jqr_AI,微信公众号:论智】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
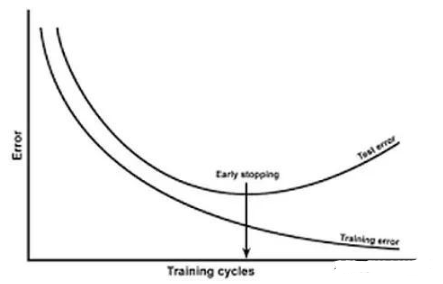
过拟合的概念和用几种用于解决过拟合问题的正则化方法





 基于镜像构建关于θ的函数,过拟合和L2正则化
基于镜像构建关于θ的函数,过拟合和L2正则化
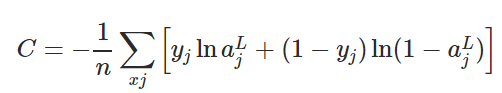










评论