线性SVM分类器通过简单地计算决策函数

背后机制

这个章节从线性 SVM 分类器开始，将解释 SVM 是如何做预测的并且算法是如何工作的。如果你是刚接触机器学习，你可以跳过这个章节，直接进入本章末尾的练习。等到你想深入了解 SVM，再回头研究这部分内容。

首先，关于符号的约定：在第 4 章，我们将所有模型参数放在一个矢量θ里，包括偏置项θ0，θ1到θn的输入特征权重，和增加一个偏差输入x0 = 1到所有样本。在本章中，我们将使用一个不同的符号约定，在处理 SVM 上，这更方便，也更常见：偏置项被命名为b，特征权重向量被称为w，在输入特征向量中不再添加偏置特征。

决策函数和预测

线性 SVM 分类器通过简单地计算决策函数

来预测新样本的类别：如果结果是正的，预测类别ŷ是正类，为 1，否则他就是负类，为 0。见公式 5-2

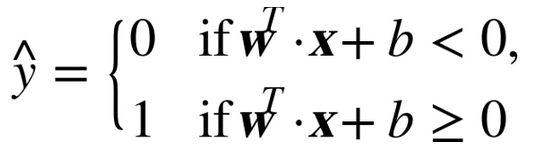
图 5-12 显示了和图 5-4 右边图模型相对应的决策函数：因为这个数据集有两个特征（花瓣的宽度和花瓣的长度），所以是个二维的平面。决策边界是决策函数等于 0 的点的集合，图中两个平面的交叉处，即一条直线（图中的实线）

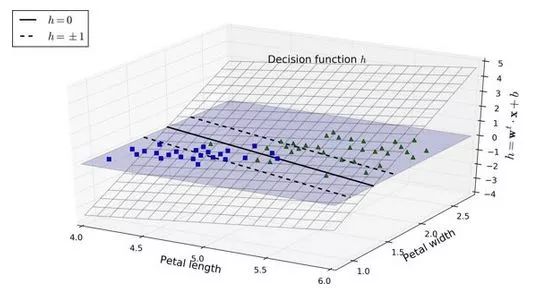
虚线表示的是那些决策函数等于 1 或 -1 的点：它们平行，且到决策边界的距离相等，形成一个间隔。训练线性 SVM 分类器意味着找到w值和b值使得这一个间隔尽可能大，同时避免间隔违规（硬间隔）或限制它们（软间隔）

训练目标

看下决策函数的斜率：它等于权重向量的范数。如果我们把这个斜率除于 2，决策函数等于 ±1 的点将会离决策边界原来的两倍大。换句话，即斜率除于 2，那么间隔将增加两倍。在图 5-13 中，2D 形式比较容易可视化。权重向量w越小，间隔越大。

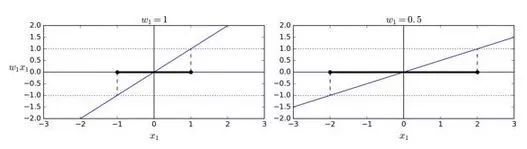
所以我们的目标是最小化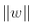，从而获得大的间隔。然而，如果我们想要避免间隔违规（硬间隔），对于正的训练样本，我们需要决策函数大于 1，对于负训练样本，小于 -1。若我们对负样本（即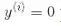）定义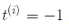，对正样本（即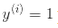）定义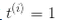，那么我们可以对所有的样本表示为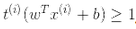

因此，我们可以将硬间隔线性 SVM 分类器表示为公式 5-3 中的约束优化问题

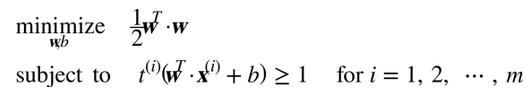
注

为了获得软间隔的目标，我们需要对每个样本应用一个松弛变量（slack variable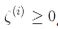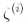） 表示了第i个样本允许违规间隔的程度。我们现在有两个不一致的目标：一个是使松弛变量尽可能的小，从而减小间隔违规，另一个是使1/2 w·w尽量小，从而增大间隔。这时C超参数发挥作用：它允许我们在两个目标之间权衡。我们得到了公式 5-4 的约束优化问题。

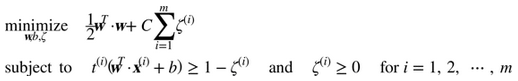
二次规划

硬间隔和软间隔都是线性约束的凸二次规划优化问题。这些问题被称之为二次规划（QP）问题。现在有许多解决方案可以使用各种技术来处理 QP 问题，但这超出了本书的范围。一般问题的公式在公式 5-5 给出。

对偶问题

给出一个约束优化问题，即原始问题（primal problem），它可能表示不同但是和另一个问题紧密相连，称为对偶问题（Dual Problem）。对偶问题的解通常是对原始问题的解给出一个下界约束，但在某些条件下，它们可以获得相同解。幸运的是，SVM 问题恰好满足这些条件，所以你可以选择解决原始问题或者对偶问题，两者将会有相同解。公式 5-6 表示了线性 SVM 的对偶形式（如果你对怎么从原始问题获得对偶问题感兴趣，可以看下附录 C）

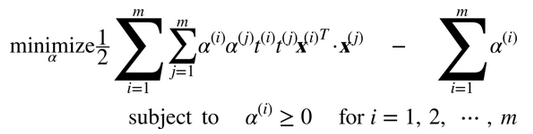
一旦你找到最小化公式的向量α（使用 QP 解决方案），你可以通过使用公式 5-7 的方法计算w和b，从而使原始问题最小化。

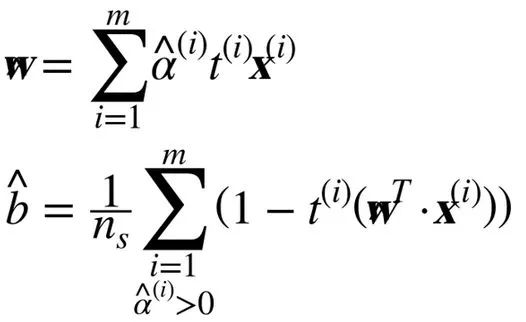
当训练样本的数量比特征数量小的时候，对偶问题比原始问题要快得多。更重要的是，它让核技巧成为可能，而原始问题则不然。那么这个核技巧是怎么样的呢？

核化支持向量机

假设你想把一个 2 次多项式变换应用到二维空间的训练集（例如卫星数据集），然后在变换后的训练集上训练一个线性SVM分类器。公式 5-8 显示了你想应用的 2 次多项式映射函数ϕ。

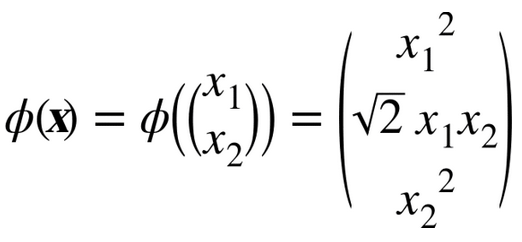
注意到转换后的向量是 3 维的而不是 2 维。如果我们应用这个 2 次多项式映射，然后计算转换后向量的点积（见公式 5-9），让我们看下两个 2 维向量a和b会发生什么。

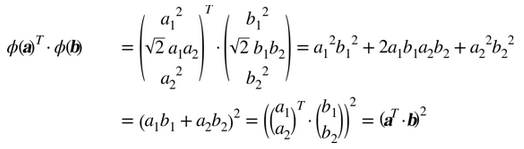
转换后向量的点积等于原始向量点积的平方：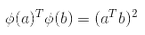

Mercer 定理

根据 Mercer 定理，如果函数K(a, b)满足一些 Mercer 条件的数学条件(K函数在参数内必须是连续，对称，即K(a, b)=K(b, a)，等)，那么存在函数ϕ，将a和b映射到另一个空间（可能有更高的维度），有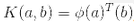。所以你可以用K作为核函数，即使你不知道ϕ是什么。使用高斯核（Gaussian RBF kernel）情况下，它实际是将每个训练样本映射到无限维空间，所以你不需要知道是怎么执行映射的也是一件好事。

注意一些常用核函数（例如 Sigmoid 核函数）并不满足所有的 Mercer 条件，然而在实践中通常表现得很好。

我们还有一个问题要解决。公式 5-7 展示了线性 SVM 分类器如何从对偶解到原始解，如果你应用了核技巧那么得到的公式会包含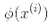。事实上，w必须和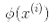有同样的维度，可能是巨大的维度或者无限的维度，所以你很难计算它。但怎么在不知道w的情况下做出预测？好消息是你可以将公式 5-7 的w代入到新的样本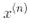的决策函数中，你会得到一个在输入向量之间只有点积的方程式。这时，核技巧将派上用场，见公式 5-11

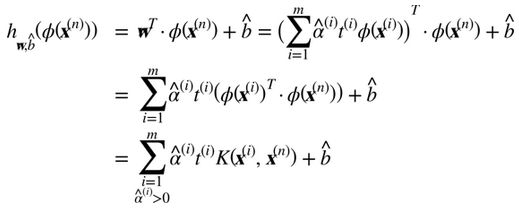
注意到支持向量才满足α(i)≠0，做出预测只涉及计算为支持向量部分的输入样本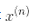的点积，而不是全部的训练样本。当然，你同样也需要使用同样的技巧来计算偏置项b，见公式 5-12

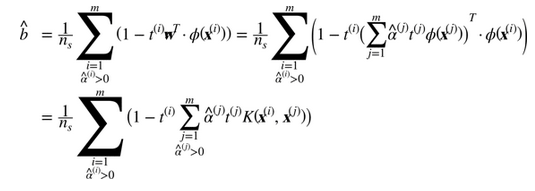
如果你开始感到头痛，这很正常：因为这是核技巧一个不幸的副作用

在线支持向量机

在结束这一章之前，我们快速地了解一下在线 SVM 分类器（回想一下，在线学习意味着增量地学习，不断有新实例）。对于线性SVM分类器，一种方式是使用梯度下降（例如使用SGDClassifire）最小化代价函数，如从原始问题推导出的公式 5-13。不幸的是，它比基于 QP 方式收敛慢得多。

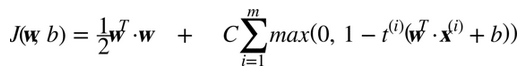
代价函数第一个和会使模型有一个小的权重向量w，从而获得一个更大的间隔。第二个和计算所有间隔违规的总数。如果样本位于“街道”上和正确的一边，或它与“街道”正确一边的距离成比例，则间隔违规等于 0。最小化保证了模型的间隔违规尽可能小并且少。

Hinge 损失

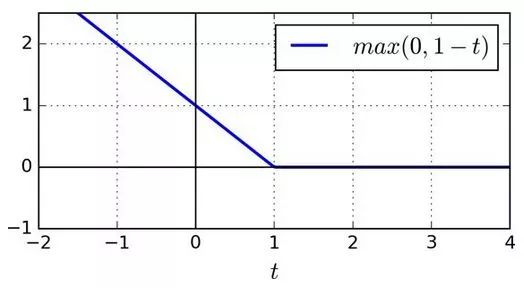
函数max(0, 1–t)被称为 Hinge 损失函数（如下）。当t≥1时，Hinge 值为 0。如果t<1,它的导数（斜率）为 -1，若t>1，则等于0。在t=1处，它是不可微的，但就像套索回归（Lasso Regression）（参见 130 页套索回归）一样，你仍然可以在t=0时使用梯度下降法（即 -1 到 0 之间任何值）

我们也可以实现在线核化的 SVM。例如使用“增量和递减 SVM 学习”或者“在线和主动的快速核分类器”。但是，这些都是用 Matlab 和 C++ 实现的。对于大规模的非线性问题，你可能需要考虑使用神经网络（见第二部分）