DeepMind最新提出“神经算术逻辑单元”，旨在解决神经网络数值模拟能力不足的问题

DeepMind最新提出“神经算术逻辑单元”，旨在解决神经网络数值模拟能力不足的问题。与传统架构相比，NALU在训练期间的数值范围内和范围外都得到了更好的泛化。论文引起大量关注，本文附上大神的Keras实现。

在昆虫、哺乳动物和人类等许多物种的行为中，表示和操纵数值的能力都是显而易见的。这表明基本的定量推理是智能（intelligence）的一个基本组成部分。

虽然神经网络能够在给出适当的学习信号的情况下成功地表示和操纵数值量，但它们学习的行为通常不会表现出系统的泛化。具体来说，当在测试时遇到训练时使用的数值范围之外的数值时，即使目标函数很简单（例如目标函数仅取决于聚合计数或线性外推），也经常会出现失败。

这种失败表明，神经网络学习行为的特点是记忆，而不是系统的抽象。触发外推失败的输入分布变化是否具有实际意义，取决于训练过的模型将在何处运行。然而，有相当多的证据表明，像蜜蜂这样简单的动物都能够表现出系统的数值外推（numerical extrapolation）能力，这表明基于数值的系统化推理具有生态学上的优势。

DeepMind、牛津大学和伦敦大学学院的多名研究人员最新发表的论文“Neural Arithmetic Logic Units”，旨在解决这个问题。研究人员开发了一种新的模块，可以与标准的神经网络结构（如LSTM或convnet）结合使用，但偏向于学习系统的数值计算。他们的策略是将数值表示为没有非线性的单个神经元。对于这些single-value的神经元，研究人员应用能够表示简单函数的运算符（例如 +， - ，×等）。这些运算符由参数控制，这些参数决定用于创建每个输出的输入和操作。尽管有这样的组合特征，但它们是可微的，因此可以通过反向传播来学习。

摘要

神经网络可以学习表示和操作数值信息，但它们很少能很好地推广到训练中遇到的数值范围之外。为了支持更系统的数值外推（numerical extrapolation），我们提出一种新的架构，它将数值表示为线性激活函数，使用原始算术运算符进行操作，并由学习门（learned gates）控制。

我们将这个模块称为神经算术逻辑单元（neural arithmetic logic unit, NALU），参照自传统处理器中的算术逻辑单元。实验表明，NALU增强的神经网络可以学习跟踪时间，对数字图像执行算术运算，将数字语言转化为实值标量，执行计算机代码，以及对图像中的对象进行计数。与传统架构相比，我们在训练期间的数值范围内和范围外都得到了更好的泛化，外推经常超出训练数值范围几个数量级之外。

这篇论文一经发表即引起很多关注，有人认为这篇论文比一眼看上去要更重要，Reddit用户claytonkb表示：“结合最近的D2NN，我们可以构建超低功耗的芯片，可以在恒定时间计算超级复杂的函数，我们很快就会转向异构计算架构。”

很快有大神在Keras做出了NALU网络的实现，感受一下：

https://github.com/kgrm/NALU

神经累加器和神经算术逻辑单元

算术逻辑单元（Arithmetic Logic Unit, ALU）是中央处理器的执行单元，是所有中央处理器的核心组成部分，由与门和或门构成的算数逻辑单元，主要功能是进行二进制的算术运算，如加减乘。

在这篇论文中，研究者提出两种能够学习以系统的方式表示和操作数字的模型。第一种方法支持累加积累量（accumulate quantities additively）的能力，这是线性外推的理想归纳偏差。这个模型构成了第二个模型的基础，即支持乘法外推（multiplicative extrapolation）。该模型还说明了如何将任意算术函数的归纳偏差有效地合并到端到端模型中。

第一个模型是神经累加器（Neural Accumulator，NAC），它是线性层的一种特殊情况，其变换矩阵W仅由-1，0和1组成；也就是说，它的输出是输入向量中行的加法或减法。这可以防止层在将输入映射到输出时更改数字表示的比例，这意味着无论将多少个操作链接在一起，它们在整个模型中都是一致的。我们通过以下方式鼓励W内的0，1和-1来改善简单线性层的归纳偏差。

由于硬约束强制W的每个元素都是{-1,0,1}中的一个，这会使学习变得困难，我们提出W在无约束参数方面的连续和可微分参数化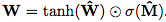：。 这种形式便于用梯度下降进行学习，并产生矩阵，其元素保证在[-1,1]并且偏向接近-1,0或1。

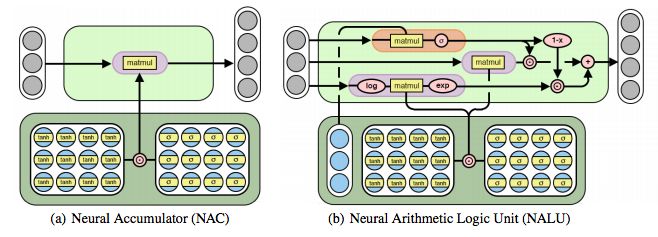
图2：神经累加器（NAC）是其输入的线性变换。 变换矩阵是tanh（W）和σ（M）的元素乘积。 神经算术逻辑单元（NALU）使用两个带有绑定权重的NAC来启用加/减（较小的紫色cell）和乘法/除法（较大的紫色cell），由门（橙色的cell）控制

虽然加法和减法使得许多有用的系统泛化成为可能，但是可能需要学习更复杂的数学函数（例如乘法）的强健能力。 图2描述了这样一个单元：神经算术逻辑单元（NALU），它学习两个子单元之间的加权和，一个能够执行加法和减法，另一个能够执行乘法，除法和幂函数，如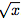。 重要的是，NALU演示了NAC如何通过门控子操作进行扩展，从而促进了新类型数值函数的端到端学习。

NALU由两个NAC单元（紫色单元）组成，这两个单元由学习的S形门g（橙色单元）内插，这样如果加/减子单元的输出值应用权重为1（on），则乘法/除法子单元为0（off），反之亦然。 第一个NAC（较小的紫色子单元）计算累加向量a，存储NALU的加法/减法运算的结果; 它与原始NAC的计算方式相同（即a = Wx）。 第二个NAC（较大的紫色子单元）在对数空间中运行，因此能够学习乘法和除法，将结果存储在m：

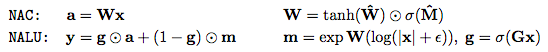
总之，这个单元可以学习由乘法，加法，减法，除法和幂函数组成的算术函数，其推断方式是在训练期间观察到的范围之外的数字。

实验和结果

我们在多个任务领域（合成、图像、文本和代码）、学习信号（监督学习和强化学习）和结构（前馈和循环）进行实验。结果表明，我们提出的模型可以学习捕获数据潜在数值性质的表示函数，并将其推广到比训练中观察到的数值大几个数量级的数值。我们还观察到，即使不需要外推，我们的模块相对于线性层也显示出优越的计算偏差。在一种情况下，我们的模型在误差率上超过了最先进的图像计数网络54%。

任务1：简单的函数学习任务

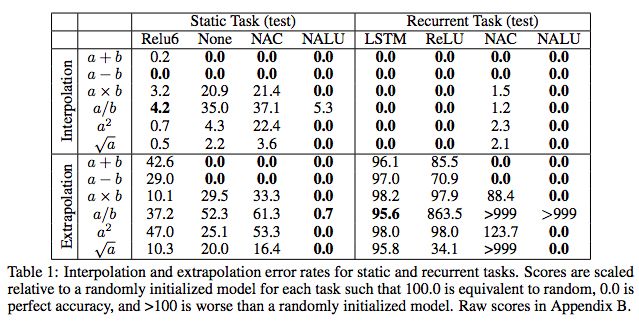
表1：静态和循环任务的插值和外推误差率。

任务2；MNIST计数和算术任务

表2：长度为1,10,100和1000的序列的MNIST计数和加法任务的准确度。

结果显示，NAC和NALU都能很好地推断和插值。

任务3：语言到数字的翻译任务

表3：将数字串转换为标量的平均绝对误差（MAE）比较。

图3：对先前未见过的查询的中间NALU预测。

图3显示了随机选择的测试实例中NALU的中间状态。 在没有监督的情况下，模型学会跟踪当前token的未知数的合理估计，这允许网络预测它以前从未见过的token。

程序评估

图4：简单的程序评估，外推到更大的值。

我们比较了三种流行的RNN（UGRNN，LSTM和DNC），结果显示即使域增加了两个数量级，外推也是稳定的。

学习在网格世界环境中跟踪时间

图5 :（上）Grid-World环境中时间跟踪任务的帧。 智能体（灰色）必须在指定时间移动到目的地（红色）。 （下）NAC提高了A3C智能体所学到的外推能力。

MNIST奇偶校验预测任务和消融研究

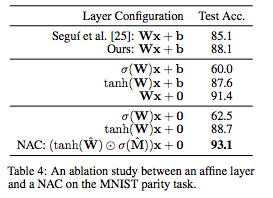
表4：关于MNIST奇偶校验任务的affine层和NAC之间的消融研究。

表4总结了变体模型的性能。结果显示，去除偏差并对权重应用非线性显着提高了端到端模型的准确性，即使大多数参数不在NAC中，NAC将先前最佳结果的误差减少了54％。

结论

目前神经网络中数值模拟的方法还不够完善，因为数值表示方法不能推广到训练中观察到的范围之外。我们已经展示了NAC和NALU是如何在广泛的任务领域中纠正这两个缺点的，它促进了数字表示和在训练过程中观察到的范围之外的数值表示函数。然而，NAC或NALU不太可能是每个任务的完美解决方案。相反，它们举例说明了一种通用设计策略，用于创建具有针对目标函数类的偏差的模型。这种设计策略是通过我们提出的单神经元数值表示（single-neuron number representation）来实现的，它允许将任意（可微的）数值函数添加到模块中，并通过学习门控制，正如NALU在加法/减法和乘法/除法之间实现的那样。