说一说信号与系统中的“归一化处理“

答疑群里面有同学问，“归一化是什么意思？”。关于数学上归一化严谨的定义我没有研究过。去网上查了一下，360百科上是这样定义的：

“ 归一化是一种简化计算的方式，即将有量纲的表达式，经过变换，化为无量纲的表达式，成为标量。 ”

不管是在信号处理类的课程中还是在工程实际中，归一化都是一种常用的处理方式。

比如，离散时间信号x(n)的自变量n，就是时间相对于采样周期（或者叫采样间隔）T的归一化，即

n=t/T

离散域的角频率（称为数字域频率）W，就是模拟角频率相对于采样频率的归一化，即：

数字域频率=模拟角频率/采样频率fs=模拟角频率×采样间隔T

在学习时域采样时，我们说：时域以T为间隔离散化，对应频域以2π/T为周期进行周期延拓，所以，抽样信号的傅里叶变换是以2π/T为周期的。但到了离散信号的傅里叶变换DTFT，又是以2π的周期的。就是因为把模拟角频率2π/T除以采样频率（即乘以采样间隔T）变成了数字域频率2π。如下图所示。

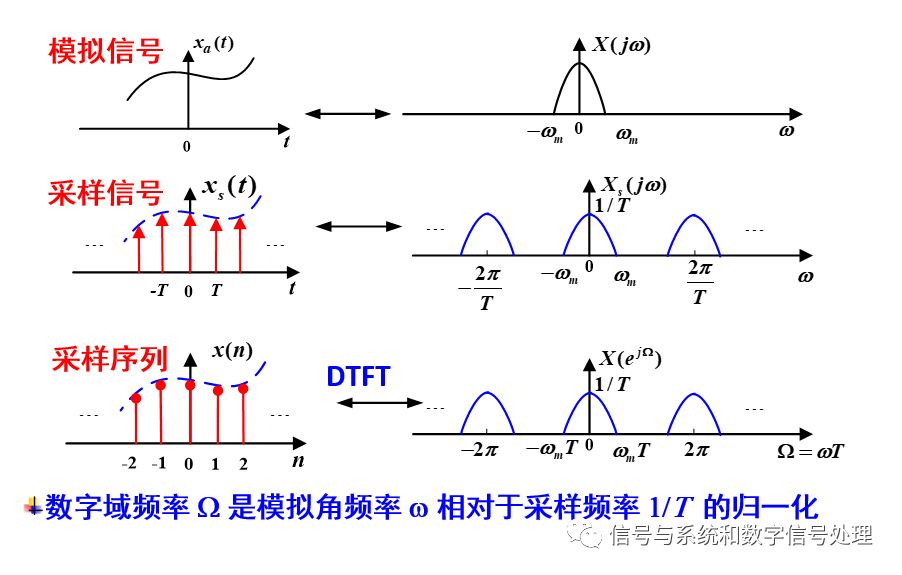
设模拟频率为f（Hz），模拟角频率就是2πf（rad/s），采样频率fs（fs≥2f），所以，数字域频率的最大值为π，如果去掉弧度，就是1。

在数字滤波器设计中，matlab中的相关函数的参数，截止频率通常限定在0~1之间，就是这个道理。对于一个采样频率为1000Hz的系统，400Hz的归一化频率就为400/500=0.8。理解这一点，不管是在学习数字信号处理，还是在工程实际中，都非常有用。

再比如，信号或者系统的幅频特性，我们信号与系统课程中，是以傅里叶变换H(jw)的模为纵轴画图，如果将其归一化，就是将|H(jw)|除以max(|H(jw)|)，也就是幅频特性的最大值为1。而在数字信号处理或者工程实际中，往往是以dB为单位画图，即：将|H(jw)|除以max(|H(jw)|)再取20倍的log。这样，幅频特性的最大值就是0dB。

比如下面这四幅图，分别是两个滤波器A和B。第一列是以归一化的|H(jw)|为纵轴，第二列，就是以归一化的dB为纵轴。看滤波器B，好像看不出来幅频特性的起伏，但以dB为纵轴，这种起伏就看的很清楚。而且阻带衰减多少个dB就一目了然。滤波器A的阻带衰减在20dB左右，而滤波器B的阻带衰减超过了40dB。从这个角度来说，滤波器B的滤波性能更优。

在数字滤波器设计中，归一化也是一种常见的思想。我们常常先设计一个截止频率为1的低通滤波器（称为归一化低通滤波器），然后通过频带变换，将其变换为所需要的滤波器。

以上内容，有些属于信号与系统，有些属于数字信号处理。

网易云课堂上线的《信号与系统》课程，同学们反映不错，也有同学希望尽快上线《数字信号处理》课程。

数字信号处理，我也上过多年，可是要做成上线的网课，我个人觉得还需要较长时间的准备。就拿已经上线的信号与系统来说吧，我从04年开始上这门课，并且参加了国家精品课程、精品资源共享课程等全程授课视频的录制（是教室实录），可以说有授课视频录制的经验，但网课和教室上课区别比较大，没有黑板，节奏也要快一些，内容全部重新梳理，课件全部重新做。从去年秋季开始准备，历经近一年的时间，直到今年暑假才全部完成。

所以，数字信号处理的网课，不能一蹴而就，我的计划是先在公众号上做，后面会陆续推出一些数字信号处理方面的文章，准备充分之后再录制成视频课。请大家谅解。