最大功率传输定理证明

最大功率传输定理概述

最大功率传输定理是关于使含源线性阻抗单口网络向可变电阻负载传输最大功率的条件。定理满足时，称为最大功率匹配，此时负载电阻（分量）RL获得的最大功率为：Pmax=Uoc^2/4R0。最大功率传输定理是关于负载与电源相匹配时，负载能获得最大功率的定理。

最大功率传输定理证明

因一个复杂的含源一端口网络可以用一个戴维南等效电路（或诺顿等效电路）来替代。下图可看成任何一个复杂的含源一端口网络向负载RL 供电的电路。设Uoc和Req 为定值，若RL的值可变，则RL等于何值时，它得到的功率最大，最大功率为多大？下面就这些问题进行讨论。从图中可知，负载RL消耗的功率pL为：

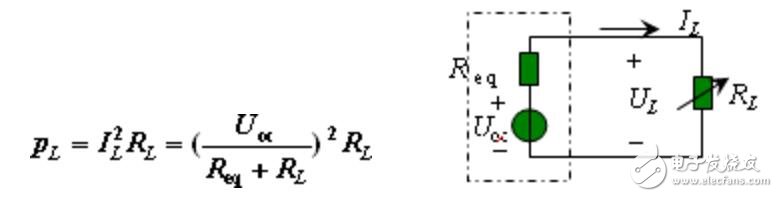
对于给定的Uoc和Req ，负载功率pL大小由负载RL决定。当RL= 0时，电流IL为最大，但因RL= 0 所以pL= 0；而当RL→∞ 时，因IL= 0所以pL仍为零，这样，只有当负载RL为某值时，必能获得最大功率，即 pL = pLmax。

由高等数学可知，欲使负载RL获得最大功率，只要满足dpL/dRL = 0的条件。将负载RL消耗的功率表达式代入得：

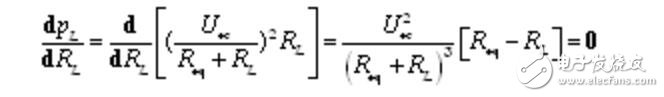
令上式为零，得 RL = Req，这时负载才能获得最大功率。这也是负载RL获得最大功率的条件。习惯上，把这种工作状态称为负载与电源匹配。在这条件下，负载电阻RL所获得的最大功率值为：

归纳以上结果可得结论，用实际电压源向负载RL供电，只有当RL= Req时，负载RL才能获得最大功率，其最大功率为：

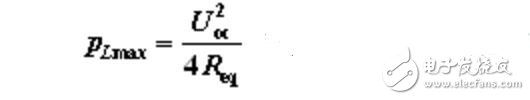
这个结论称为最大功率传输定理。

最大功率传输定理内容

最大功率传输定理是关于负载与电源相匹配时，负载能获得最大功率的定理。定理分为直流电路和交流电路两部分，内容如下所示。

直流电路

含源线性电阻单口网络（）向可变电阻负载传输最大功率的条件是：负载电阻与单口网络的输出电阻相等。满足条件时，称为最大功率匹配，此时负载电阻RL获得的最大功率为：

交流电路

工作于正弦稳态的单口网络向一个负载供电，如果该单口网络可用戴维宁（也叫戴维南）等效电路（其中）代替，则在负载阻抗等于含源单口网络输出阻抗的共轭复数（即电阻成份相等，电抗成份只数值相等而符号相反）时，负载可以获得最大平均功率。这种匹配称为共轭匹配，在通信和电子设备的设计中，常常要求满足共轭匹配，以便使负载得到最大功率。

最大功率传输定理使用范围

满足最大功率匹配条件（）时，Ro吸收功率与RL吸收功率相等，对电压源uoc而言，功率传输效率为。对单口网络N中的独立源而言，效率可能更低。电力系统要求尽可能提高效率，以便更充分地利用能源，不能采用功率匹配条件。但是在测量、电子与信息工程中，常常着眼于从微弱信号中获得最大功率，而不看重效率的高低。