引 言
智能电表(smart meter)作为智能电网的终端计量仪器,不仅需要能够精确计量用户的用电信息,而且还需各种通信功能,如RS485.红外。电力线载波等,以实现自动化远程管理。因此,智能电表在整个智能电网的建设中起着关键性作用。而对于智能电表的核心---电能计量专用芯片(Electrical Measurement Unit,EMU)也提出了更高的要求。目前计量芯片的模数转换电路基本上都采用Sigma-Delta 型,而降采样滤波器是Sigma-Delta ADC 的核心组成部分,因此,对降采样滤波器的研究具有十分重要的意义。
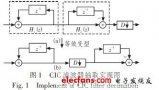
在Sigma-Delta ADC 中,功耗主要集中在降采样滤波器 。而滤波器的功耗主要由乘法器决定,因此如何减少滤波器中乘法器的个数成为降采样设计的研究重点.HOGENAUE 提出了级联积分梳状滤波器(Cascaded Integrator Com,CIC),由于CIC滤波器无须乘法运算,因此与传统通过FIR 滤波器直接降采样相比,极大地降低了面积与功耗。然而当降采样率较大时,单级CIC 滤波器却无法满足要求,且功耗也相对较大。多级采样交换理论及多相原理从而降低乘法运算次数,该方法的难点在于多相因子的不确定性,且不同的多相因子得到的滤波器结构不一样,功耗也不一样。串行算法实现CIC 从而降低功耗,但串行方法不适合计量芯片中并行的数据处理。文中提出了一种级联抽取的方法,不仅结构简单,也易于实现,完全满足电能计量的需求。前级为CIC 滤波器,后级为HBF 滤波器,实现128 倍的抽取。由于HBF 只适用于2 倍抽取,因此前级CIC 降采样率为64 倍。对HBF 的非零系数采用有符号CSD 编码,进一步减少了电路功耗。
1 CIC 滤波器原理及设计
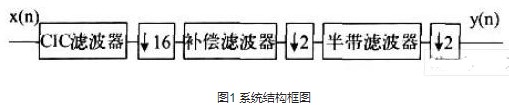
CIC 滤波器的基本结构如图1 所示,由积分级和梳状级级联组成。

积分级采样频率为FS ,它的传递函数:
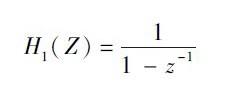
降采样的倍数为R,相对于积分级,梳状级的采样频率为FS / R,它的传递函数:
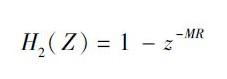
其中M 为延迟因子,控制梳状级的频率响应,在设计中,M 的取值一般为1 或2.
假设CIC 滤波器有N 阶,那么总的传递函数为 :
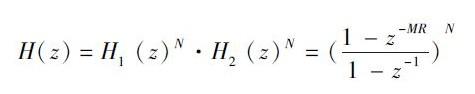
幅值响应为:
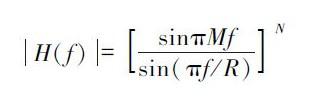
CIC 滤波器的优点是结构非常有规律,由若干级积分级与梳状级级联组成,且内部无须乘法运算,因此,在变速率系统中得到了广泛的应用。但随着降采样率的增加,内部寄存器的宽度以及功耗将会成倍的增加。电能计量芯片Sigma – Delta 的采样频率为1792kHz,后续数字信号处理的频率为14kHz,因此,在本设计中,为了实现128 倍的降采样,采用了分级抽取的方法。降采样滤波器的总体框架如图2 所示 。
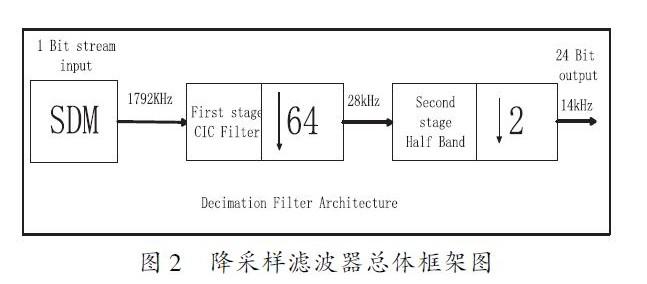
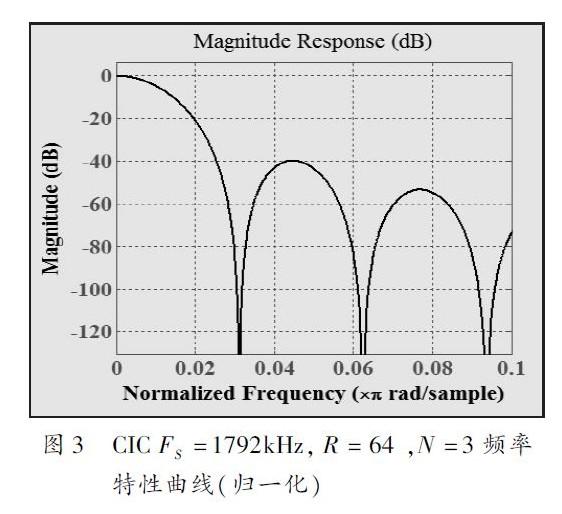
由于Σ-△为二阶调制器,因此,三阶CIC 滤波器即可达得很好的抽取效果。假定延迟因子为1,则内部寄存器的长度L = (N*(log2R ) + 1) 为19bit.采样定点算法,内部寄存器量化为Sfix34. En15,输出为Sfix24. En23.由CIC 滤波器的结构以及幅值响应公式可知,当R 足够大时,信号通过CIC 滤波器时,幅值将会被放大[RM]N 倍,此设计中为643 ,因此,需将CIC输出右移18 位,消除增益对信号的影响。图3 为通过MATLAB 仿真得到FS =1792kHz, R = 64,N = 3 的归一化(0 - 0. 1)幅频特性曲线。
2 半带滤波器的设计
第二级的抽取滤波器用于衰减经过第一级梳状滤波器后混叠在基带内的信号分量和量化噪声分量。由于电能计量对信号有严格的线性相位要求,所以必须采用FIR 型滤波器。半带滤波器是一种特殊的线性相位滤波器,它的偶数系数都为零(中间位系数为0. 5),因此其实现滤波的运算量与同样长度的其它线性相位滤波器相比减少一半,这将进一步减小芯片面积。降低电路的功耗。
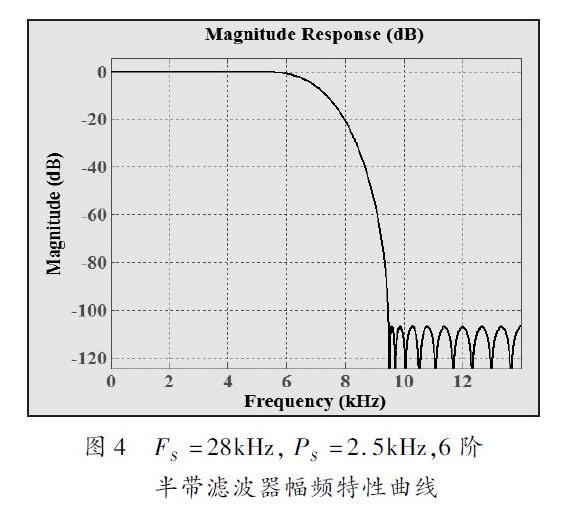
综合考虑芯片面积以及系统的频率响应,HBF 设定为6 阶。考虑到正弦信号的高次谐波以及CIC 补偿滤波器的通带频率,HBF 的通带频率设定为2. 5kHz.
由于HBF 的系数值很少,量化精度不够将影响系统的传输特性,仿真到的系数采用Sfix48. En47 Bit,内部乘法器采用Sfix56. En55 Bit 可满足系统要求,而考虑到补码定点数加法有可能产生溢出,所以加法器量化为Sfix56. En54 Bit.图4 为通过MATLAB 仿真得到的HBF 幅频特性曲线。
HBF 的运算包括乘法以及加法,而乘法运算的功耗最大。传统的乘法运算采用移位相加的原理,相加次数等于乘数中1 的个数,因此减少乘数中1 的个数即可降低乘法电路的功耗.CSD 编码正好满足这一要求,经过CSD 编码后,将乘法系数中1 的个数降到最低,从而减少加法(或减法)的次数.CSD 编码含三重值{1,0,-1},编码原则是从最低有效位开始,用100…0(-1) 来取代所有大于2 的1 序列。例如上述HBF中乘法系数b (3)= 0. 28847028573567002,量化后b(3)= 48′h24EC98258D1E(Sfix48_En47),则对应的CSD 编码b (3)= 0+00+0+000-0-00+0+0-00000+0+0-0-00+0-0+00+000-0(“+”表示1,“-”表示负1)。
x(n)*b(3) = – (x(n) 《 《 1) + x(n) 《 《 5 + x(n)《 《 8 – (x(n) 《 《 10) + x(n) 《 《 12 + … + x(n)《 《 40 + x(n) 《44,因此,经CSD 编码后, b (3)的乘法运算变成只有10 次加法和7 次减法运算,与传统的移位相加相比,减少了运算的次数,从而降低了HBF 的功耗。
3 补偿滤波器的设计
从图3 可以看出,CIC 滤波器幅频特性曲线在通带内并不平坦,在通带内信号被衰减。为了克服这一缺点,可加入补偿滤波器,它的幅频特性正好与CIC 滤波器相反,完成对频率响应的补偿,从而扩展了系统的频率特性。
补偿的基本原理是使通带内信号的衰减为零。补偿滤波器的幅值响应与(4)式相反。

当R 足够大时,补偿滤波器的响应接近反SINC 函数,因此补偿滤波器也称之为反SINC 滤波器。
补偿滤波器一般可借助MATLAB 仿真,再与CIC滤波器级联观察补偿后总的频率响应是否满足系统要求,从而得出补偿滤波器的参数。图5 为图3 中CIC滤波器加入补偿后的幅频特性曲线图。

在图3 中,衰减点在1kHz 左右,而从图5 中可以看出,加入补偿滤波器后,衰减点出现在2. 5kHz 左右,因此,补偿滤波器可以很好地克服由于CIC 滤波器在通带内幅值衰减的问题。
补偿滤波器的采样频率为CIC 滤波器降采样后的频率( FS / R),为了避免频率混叠,其截止频率的最大值为采样频率的一半:FC = (FS / R) / 2.在实际应用中,为了得到更加理想的频率特性,截止频率一般设定为采样频率的四分之一,即FC = (FS / R ) /4.
4 实验数据以及结论
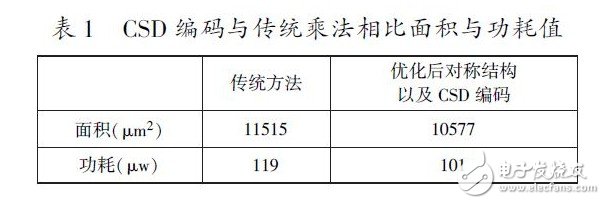
本设计针对电能计量芯片.Sigma-Delta 的采样频率为1792kHz,数字电路工作时钟为14kHz.CIC 滤波器的降采样率R =64.根据经验,当CIC 滤波器的阶数比Sigma-Delta 调制器的阶数高一阶时可以达到较好的效果,因此,本CIC 滤波器设定为3 阶,延迟因子为1.半带滤波器采样频率为28kHz,通过MATLAB仿真,6 阶通带频率为2. 5kHz 可以满足系统要求。在实验过程中利用Verilog HDL 语言,HBF 采样对称结构以及CSD 编码,在CSMC 0. 18μm 工艺下综合,得到面积与功耗如表1 所示。
5 结束语
本设计根据电能计量芯片的要求,对Sigma-Delta降采样滤波器进行优化设计。由于单级CIC 滤波器在实现高倍降采样率时功耗大,效果不理想,因此,本设计对128 倍的降采样进行分级抽取,前级采用CIC 滤波器进行64 倍抽取,后级采用半带滤波器实现2 倍抽取。在HBF 的实现过程中采用对称结构以及CSD 编码,减少运算过程中乘法的次数以及乘法运算过程中移位相加次数,降低了电路功耗。与传统方法相比,经优化后,电路面积减少8% ,功耗降低15% .
-
芯片
+关注
关注
456文章
50955浏览量
424784 -
智能电网
+关注
关注
35文章
2932浏览量
116342 -
滤波器
+关注
关注
161文章
7846浏览量
178404
发布评论请先 登录
相关推荐
求助,AD7190关于Σ-Δ ADC其中的抽取滤波器的数据转换问题求解
Σ-Δ ADC数字滤波器类型
数字下变频中抽取滤波器的设计及FPGA实现
FPGA的FIR抽取滤波器设计详细教程
关于高频数字抽取滤波器的设计
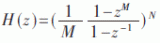
基于FPGA的_ADC数字抽取滤波器Sinc_3设计

ADC数字下变频器:抽取滤波器和ADC混叠,第1部分




 应用于电能计量芯片中Σ-△ADC的数字抽取滤波器的设计
应用于电能计量芯片中Σ-△ADC的数字抽取滤波器的设计











评论