1 、研究背景
随着半导体器件的尺寸不断缩小,集成电路(IC)设计的规模越来越大,芯片集成度越来越高,使得芯片测试越来越困难。为了提高集成电路的成品率,研究人员把更多的精力放在芯片的测试技术上,试图采用更简便有效的方法测试芯片,并获得满足要求的故障覆盖率。
电路故障覆盖率的*测方法可以在芯片制造完成后,通过自动测试仪(ATE)获得芯片的故障覆盖率。这种方法是一种事后的*估行为,他只能对成品芯片的优劣做出估计,不能对改进芯片设计起到至关重要的作用。
另一种获得故障覆盖率的方法是,设计或测试人员在进行电路功能仿真(前仿真)或电路时序仿真(后仿真)的过程中,对电路注入单故障或多故障,然后在电路存在故障的情况下,模拟电路的行为,确认该故障是否会导致电路产生差错或失效。对所选定的故障集中的所有故障进行模拟后,就可以获得电路的故障覆盖率。对于门级电路,故障注入的位置可以是门电路的输入或输出线。这种方法对改进电路设计有直接的效果。
2、 故障与故障注入
故障覆盖率是给定测试集所能检测的给定电路在给定的故障模型下的故障数与电路中含有的故障总数之比。
比较常见的故障模型有固定型故障和桥接故障,桥接故障会改变电路的拓扑结构,本文主要讨论的是固定型故障。固定型故障主要反映电路或系统中某一根信号线上信号的不可控,即系统运行过程中该信号线永远固定在某一个值上。故障注入是指按照选定的故障模型加于运行特定工作负载的目标系统中,用人工的方法有意识地产生故障并施以加速该系统的错误和失效的发生,同时观测和回收系统对所注入故障的反应信息,并对回收信息进行分析,从而向试验者提供有关结果的试验过程。
3、 电路故障响应分析程序设计
3.1 确定型测试
本程序采用确定型测试,即为被测电路的每个故障产生相应的测试码,生成一个能测试电路中所有故障的测试码集合作为测试码源,无故障电路对应于测试码中的各个测试的响应值存储起来作为参考值,如图1所示。可以采用公式的方法对测试码进行更准确的定义。
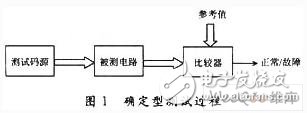
X:被测电路的可控输入矢量;
G(X):电路无故障时的可测输出矢量;
Gf(x):电路有故障f时的可测输出矢量;
测试和测试码:一个输入矢量A,满足G(A)≠Gf(A);
故障的完全测试集:所有满足G(A)≠Gf(A)的输入矢量的集合。
这里有定理,一个电路中所有的单固定型故障都是可测的,当且仅当该电路是无冗余的。本程序采用最小完全测试集(含有最小测试数的完全测试集)作为测试码。
3.2 输入电路
选用的输入为ISCAS85基准电路。他是电子自动化关于IC测试的标准,85指组合电路,89指时序电路。
3.3 注入单故障的分析
程序共分以下4个重要步骤:
(1)初始化网表
首先读入电路的门级电路的描述的ISCAS85电路网表,对其进行文本修改,将其变成便于程序运行的格式。
(2)载入测试向量
测试向量的最小完全测试集存储在.test为后缀名的文件中,载入后以ver.out为后缀名的文件输出。
(3)无故障时电路输出
输入测试向量到注入故障前的电路,得到无故障电路时对于测试向量的正确输出作为参考值,将结果存储在fault_free_output.out文件中。以for(p_tr=0;p_tr
(4)故障注入
首先一个循环是对于整个故障集for(p_f=0;p_f
根据以上结果做统计工作,写文件fault_list.out和fault_sum.out。写文件fault_list.out是在每次循环for(p_no=1;p_no
根据数据得到程序最后需要的统计结果,即故障响应率。其计算公式为:
sum of error/(refss*tlotv)
sum of error是注入单故障之后,对于测试向量集,得到的结果与参考值不同的次数;srefss是simplistically reduced equivalent fault set size的缩写,即最小等价故障类的大小;tlotv是the length of test vectors的缩写,即测试向量的个数。
3.4 注入双故障的分析
在进行注入单故障情况下的分析以及得出结果故障响应率(FRF)后,继续考虑对ISCAS85基准电路注入双重故障的情况进行研究。
注入双故障,基本的思想就是在注入一个单故障的情况下,再注入一个与之不同的故障,其等价效果极为注入双故障。所以在fault_injection增加1层循环,即:
for(p_f=0;p_f
从而由原先的整个故障集-整个测试向量-遍历网表每一行的3层嵌套循环,扩展为整个故障集-整个故障集-整个测试向量-遍历网表每一行的4层循环。当然另外在便利网表时要注入双重故障,即要判断此节点是否时注入故障的那2个节点以及注入的是故障0还是故障1,进行响应的操作。
注入双故障时的故障响应率(FRF)的计算公式为:
sum of errot/{[srefss*(srefss-1)]*tlotv}
4 、结 语
根据各个电路的输出结果,结合上面的计算参数,就可以得到注入单故障的故障响应率(FRF)。如表2所示。
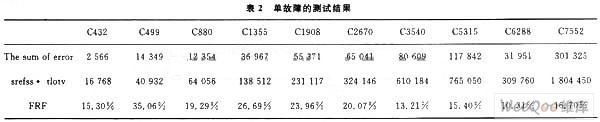
对于注入单故障的故障响应率(FRF)的分析可以从两个方面来看:从故障注入的角度,他反映了注入故障之后的电路,对于测试向量的响应情况,故障响应率越高,说明这组测试向量对电路的故障检测能力越强;但是如果从容错的角度来看,故障响应率(FRF)越低,说明更多情况下,即使电路中存在故障,也可以得到正确的输出结果,说明的电路具有比较强的容错能力。
同样,结合注入单故障时的计算参数srefss和tlotv,得到注入双故障的故障响应率(FRF)。如表3所示。
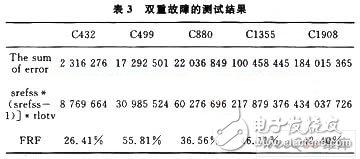
从此组数据可以看出,注入双重故障下的故障响应率比注入单故障是的故障响应率有明显的增大,增加1倍左右。这个结果是可以理解的,从故障响应的角度,一组测试向量在双故障情况下其故障响应能力明显提高(因为输出结果出错的几率大大增加);而从容错的角度来看,电路能够容纳双故障的能力一定会大大降低,导致故障响应率的提高。
-
芯片
+关注
关注
455文章
50844浏览量
423835 -
半导体
+关注
关注
334文章
27382浏览量
218967 -
仿真
+关注
关注
50文章
4086浏览量
133639
发布评论请先 登录
相关推荐
后驱动技术在故障注入中的退化机理的研究
PXI故障注入开关模块应用于故障注入测试
如何为波特图设置频率响应分析仪
运行时软件故障注入器的设计与实现
分布式星载系统故障注入研究
基于FPGA的容错计算机故障注入研究
Moku:Lab频率响应分析仪的应用指南
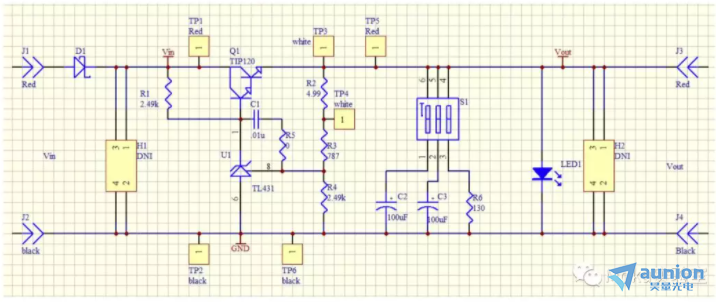
电源稳定性分析-Moku:Lab频率响应分析仪应用指南





 基于故障注入的数字电路故障响应分析
基于故障注入的数字电路故障响应分析











评论