通过利用编程语言LabVIEW实现数字变频FFT的频谱细化算法设计

引 言

在运动目标速度测量中，常利用频谱分析的方法获取目标的多普勒频率，并依据多普勒测速原理来完成动目标速度测量。为达到高精度测速的要求，需进一步提高频率分辨率，在实际频谱分析中，要对获取的试验数据先进行分段处理，在此基础上再进行细化操作，这样可获得比常规FFT分析更高的频率分辨率。近年来，频谱细化技术发展迅速，常见的方法有：HR-FA法，基于多相滤波器的ZFFT法，基于复调制的Zoom-FFT法，自适应Zoom-FFT法，Chirp-Z变换和小波基法等。然而，这些频谱细化技术普遍存在运算量大，不易实现编程的缺点。为此，提出了一种数字变频FFT的频谱细化算法，并利用图形化编程语言LabVIEW进行了编程设计。

1数字变频FFT的数学原理

在频谱分析中，频率分辨率表示频谱中能够分辨的两个频率分量的最小间隔，用频率间隔△f表示为：

要提高FFT的频率分辨率，可通过以下两种途径实现：

(1)降低采样频率fs。这会使频率分析范围缩小，其降低的幅度受到采样定律的限制。

(2)需要增加分析的采样点数N。这意味着计算机的存储量和计算量大大增加，由于实际系统软、硬件方面的限制，这样做并不总是可能的。

可以看出以上两种方法提高频率分辨率的能力有限且灵活性差。所用的数字变频FFT主要指采用移频特性进行频谱细化的技术，其原理框图如图1所示。

设模拟信号为x(t)，经A／D转换后得到采样时间序列x(n)(n=0，1，…，N-1)，设fs为采样频率；f1～f3为细化分析频带；f0为需要细化的频带中心频率；D为细化倍数；N为FFT分析的点数，算法如下：

(1)复调制移频

所谓复调制移频就是将频域坐标向左移或向右移，使得被观察的起点为频域坐标的零频位置。这里对离散信号x(n)用exp[-2πf0／fs]进行复调制，把需要细化的频带起点移至频率轴原点，得到：

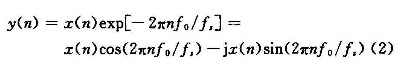
(2)数字低通滤波

为保证重新采样后不发生频谱混叠，必须进行抗混叠滤波，以滤出所需分析频段信号。设频率细化倍数为D，则低通滤波器的截止频率fc=fs／2D。

(3)重新采样

信号被移频和低通滤波后，分析信号频带变窄，因而可以以较低的采样频率fs=fs／D进行重采样，fs比原采样频率降低了D倍，即对原采样点每隔N点再抽样一次。

(4)反移频处理

实行反移频操作就是将频率中心重新移到需要细化的频带起始频率，使得移频前后的频率保持一致。

(5)FFT运算

对反移频后的信号进行FFT处理，得到细化后的频谱，其频率分辨率提高了D倍。

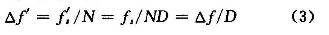
2数字变频FFT的LabVIEW实现

2.1虚拟仪器LabVEW

LabVIEW是美国NI公司推出的虚拟仪器开发平台软件，是一种非常优秀的面向对象的图形化编程语言，用于快速创建测试、测量和控制应用程序。它的优点是数据处理速度快，硬件支持等方面功能强大；缺点是在数值处理、分析和算法工具等方面的效率不高。而MathWorks公司开发的Matlab提供了强大的矩阵运算和图形处理功能，编程效率高，特别擅长数值分析和处理，但其界面开发能力较差，不能进行实时操作和控制。

鉴于LabVIEW和Matlab两种语言的优点，在虚拟仪器开发过程中，除利用LabVIEW直接编程外，还可结合Matlab进行混合编程。通常用LabVIEW设计用户图形界面，负责数据采集和网络通信；Matlab在后台提供大型算法供LabVIEW调用。

2.2 LabVIEW直接编程实现数字变频FFT

在LabVIEW直接编程中，通过调用Ramp Pattern.vi节点和Exponential.vi节点完成信号的复调制和反移频操作；通过调用Decimate.vi节点对复调制后的信号进行滤波，压缩频带，然后进行整数倍抽取。其中，对信号进行数字低通滤波的滤波器为切比雪夫I型滤波器，其主要参数：阶数为8阶，截止频率为0.8·(fs／2)／D；通过调用FFT.vi和Array Size.vi节点完成FFT运算，辅以其他相应的计算处理节点，根据数字变频的原理图最终实现数字变频FFT，其程序框图如图2所示。

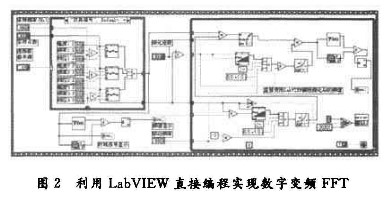
2.3 LabVIEW与Matlab混合编程实现数字变频FFT

LabVIEW与Matlab的混合编程，可通过调用LabVIEW中的Matlab Script节点实现。其中，MatlabScript节点本身具有多输入、多输出的特点，一次处理的信息量可以很大。在Matlab中，根据数字变频FFT的数学原理，编程实现复调制移频、低通滤波、重采样、反移频和FFT操作处理，经调试无误后，导入到Matlab Script节点中；然后在LabVIEW中，通过调用SineWave.vi产生仿真信号，或从文件中读取信号数据，同时添加采样频率，细化倍数等控制节点；最后连接各图标，实现数字变频FFT，其程序框图如图3所示。

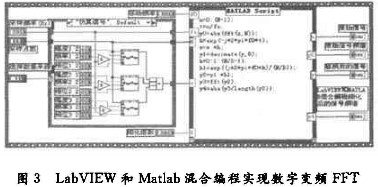
3仿真分析

利用LabVIEW编程实现数字变频FFT软件处理平台，调用Functions＼Analyze＼Signal Processing＼Signal Generation子模板中的Sine Wave.vi创建正弦信号发生器，构造仿真信号：

x(t)=sin(2πf1t)+2sin(2πf2t)+5sin(2πf3t)

式中：f1=2 002 Hz；f2=2 004 Hz；f3=2 006 Hz；采样点数N=5 120；采样频率为51 200 Hz。根据式(1) 可知，此时频率分辨率为10 Hz，在频域内分辨不出这3个信号。

若要把分辨率提到1 Hz，即细化10倍，就要采样51 200个点，然后把分析频带(2 000～2 010 Hz)的起始频率f=2 000 Hz点移到原点，当细化倍数D=10时，即51 200个采样点每隔10个点进行抽取，完成对复调制移频、滤波后的信号重采样。新的采样频率即为5 120 Hz，降低了10倍，抽取得到5 120个点。为了使细化后的频率与细化前的一致，在作FFT前应该实行反移频，这样就可以得到分析频带上的细化频谱。如果采用LabVIEW直接编程处理，其细化频谱如图4所示；如果采用LabVIEW和Matlab混合编程处理，其细化频谱如图5所示。

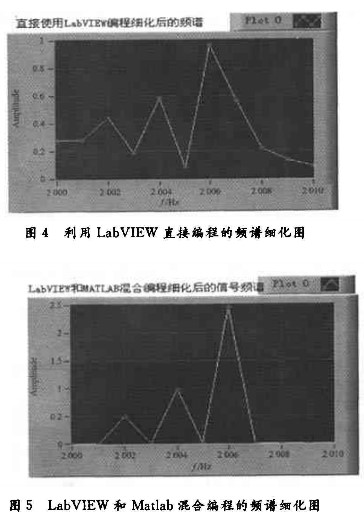
从图4和图5中可以看出，基于LabVIEW的两种编程方法都实现了频谱细化的功能，2 002 Hz，2 004 Hz和2 006 Hz三个频率点对应的幅值谱清晰可见，且幅值相差2.5倍，分辨率为1 Hz。

4结语

数字变频FFT是频谱分析中一种约束条件少，可操作性强的方法。在此借助功能强大的LabVIEW软件编程处理方法，使得数字变频实现简便，能够满足提高频率分辨率的要求，并具有很高的实时性。

显然，在动目标速度测量中，利用数字变频FFT进行频谱细化处理，可获得更高的频率测量精度。根据多普勒原理，也可获得更高的测速精度。因此，研究中基于LabVIEW的数字变频FFT频谱细化方法在工程实践中有着重要的应用价值，可广泛应用于汽车、飞机等运动目标的速度测量中。