耦合机构沿轨道相对运动时，ICPT系统能够保持良好的平稳性

摘要：

设计了发射线圈平面缠绕和发射线圈竖直缠绕这两种不同的耦合结构，通过分析选择了一种传输功率大的耦合机构，并研究了这种耦合机构在接收线圈沿轨道运动时非接触电能传输的平稳性状况。借用ANSYS有限元仿真工具，得到这两种耦合结构耦合线圈的自感及互感，再仿真这种耦合机构沿轨道相对运动时传输功率的变化情况。实验中制作了这两种耦合机构，最后选用了一种传输能力强的耦合机构，使其沿轨道水平运动，结果表明系统能够保持良好的平稳性。

0 引言

感应耦合式非接触电能传输(Inductive Contactless Power Transfer，ICPT)是一种电源与负载之间没有直接的电气接触能量传输方式，不会产生电火花，避免了导线拖拽带来的不便，减少了有线供电存在的安全隐患[1]。因此，ICPT在一些特殊的场合下有着广泛的应用前景，比如应用在电动汽车的无线充电以及在一些起重运输的设备上[2-4]。

针对ICPT的耦合机构，国内外许多研究机构对此进行专门的研究。以新西兰BOY T教授为首的课题组提出了一种E型耦合结构，这种耦合结构的初次级线圈耦合紧密、效率高、传输功率大[5-6]。文献[7]针对电动汽车无线充电，为使耦合机构提供一个较大的充电区域，设计了一种DLDD（Double Layer Double D-type）形式的耦合线圈。文献[8]中又提出一种新型的耦合结构——H型结构，该机构具有效率高、横向位移范围大和质量轻等特点。以上文献中均未对耦合机构沿轨道相对运动时，ICPT系统的平稳性进行研究。

本文利用ANSYS有限元软件并设计了实验，最后得出在耦合机构沿轨道相对运动时，ICPT系统能够保持良好的平稳性的结论。

1 沿轨道相对运动的耦合结构

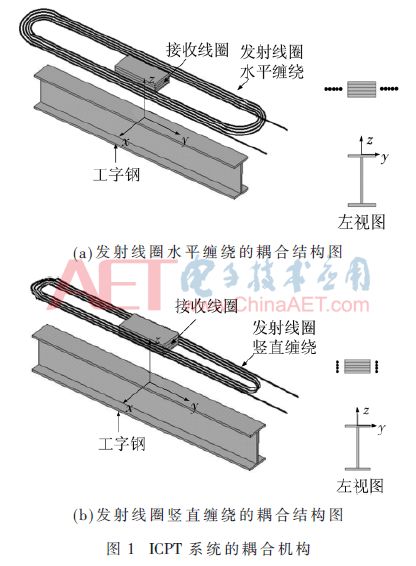
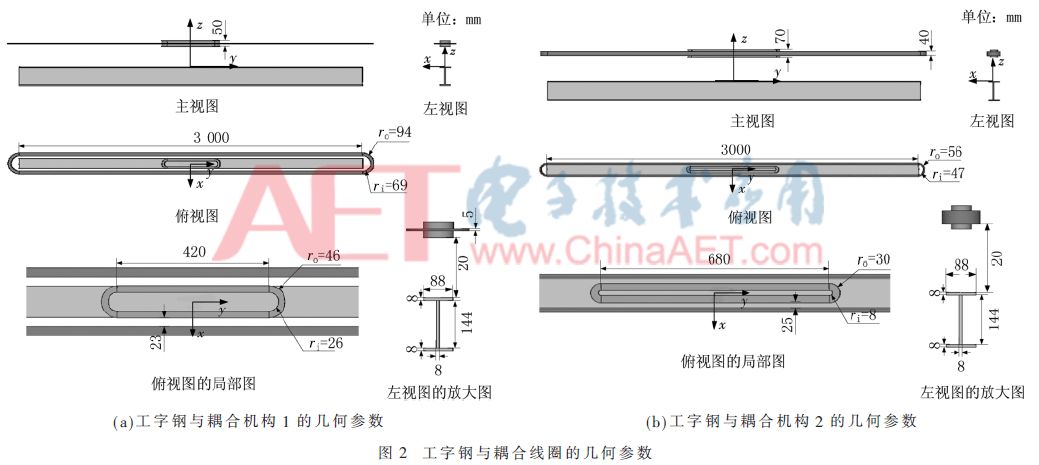
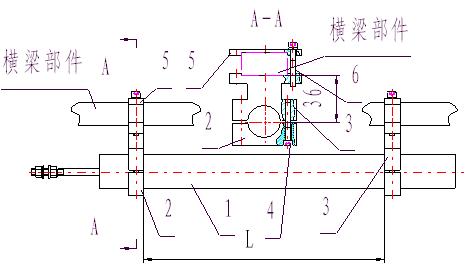
本文以起重运输设备为背景，为了便于对比，设计并制作了两种耦合结构沿轨道相对运动的ICPT系统，如图1所示，在后文分别称为耦合机构1和耦合机构2，它们的几何参数如图2所示。两者主要区别是，耦合机构1的发射线圈是水平缠绕，而耦合机构2的发射线圈是竖直缠绕。其支撑框架均为木材和有机玻璃框架，发射线圈固定在起承重作用的工字钢梁上，接收线圈与其他所有接收装置沿工字钢横梁做水平直线运动。因而，发射线圈与接收线圈存在长距离的相对运动。

2 理论分析

2.1 耦合线圈参数的理论分析

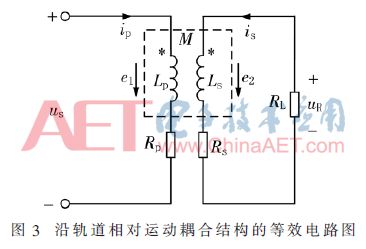
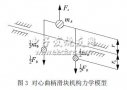
基于ANSYS有限元仿真得到的结果，通过ICPT系统的等效电路模型分析可得到耦合线圈的自感及互感。图1中所表示的沿轨道相对运动耦合结构的等效电路图如图3所示。

式(2)是一个复数方程组，根据互感线圈二端口输入、输出能量守恒，可推出式(2)中只有3个实数方程线性无关。因此式(2)中Lp、Ls和M有唯一解。

2.2 非接触电能传输系统的传输功率

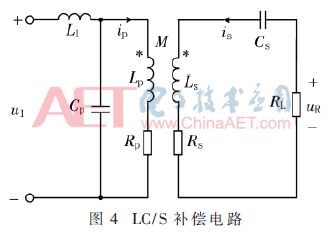
本文采用LC/S网络补偿方式，其补偿电路图如图4所示，将接收端等效到发射端，再将发射端电路用诺顿电路等效，其等效电路图如图5所示，Zeq为接收端等效到发射端的等效阻抗。

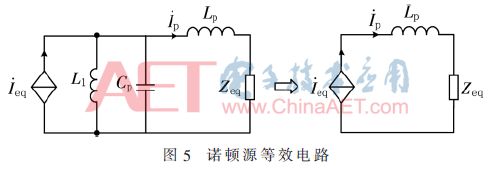
其诺顿等效源为：

将图4中接收侧回路用受控源回路等效，如图6所示。

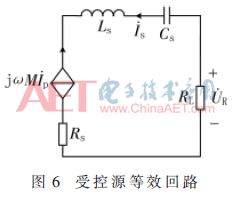
接收侧回路满足：

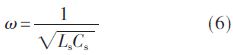
因此，ICPT系统的传输功率为：

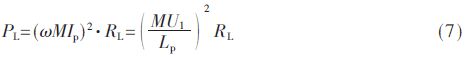
3 耦合机构的仿真结果

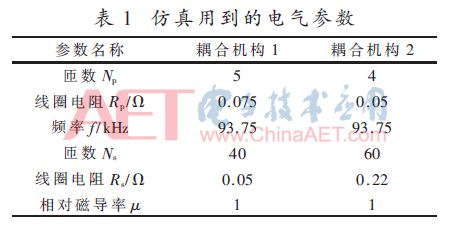
本文使用通用电磁场仿真工具ANSYS有限元软件，对上述这两种耦合机构进行仿真。设定耦合机构中发射线圈距工字钢距离d=20 cm，电源电压Us=351 V，负载电阻RL=68 Ω，仿真中所用到的电气参数如表1所示。工字钢相对磁导率μ为4 000，电阻率为20×10-8Ω/m。

3.1 两种耦合机构传输能力的比较

利用耦合线圈与工字钢结构对称特点，采用其二分之一结构模型。借用ANSYS有限元仿真软件，得到如图7所示耦合线圈感应电动势的实部，同理，还可得到耦合线圈感应电动势的虚部及负载电压。图7是耦合机构1接收线圈处于中间的位置。

因此，通过ANSYS有限元仿真可得出发射线圈和接收线圈的感应电动势及负载电压。根据第2部分的理论推导，可得耦合机构线圈的自感和互感如表2所示。

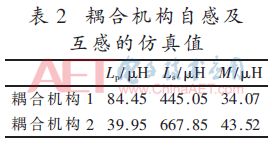
由表2可知，耦合机构1的M1/Lp1=0.4，耦合机构2的M2/Lp2=1.1，而系统的传输功率正比于M与Lp比值的平方，即耦合机构2比耦合机构1的传输能力强，因此，下面将对耦合机构2沿轨道相对运动进行ICPT的平稳性研究。

3.2 耦合机构2沿轨道相对运动

下面研究耦合机构2沿轨道相对运动时，ICPT功率的变化情况。分为以下3种情况：(1)接收线圈相对于发射线圈沿水平方向运动；(2)接收线圈相对于发射线圈在竖直方向上有偏离；(3)接收线圈在发射线圈内前后侧方向上有偏离。

为了消除系统的无功损耗，减小回路阻抗，需要在接收回路中串联补偿电容。耦合机构2中接收线圈的自感Ls2=667.848 μH，根据串联谐振公式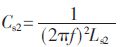：s2≈4.32 nF。由于串联补偿电容的影响，导致接收侧回路中的交流电流i2的变化很大，这样工字钢会反过来影响耦合线圈的自感，因此根据Ls2=667.848 μH计算出来的串联谐振电容Cs2≈4.32 nF并不是最佳的补偿电容值。可从优化方法的思想，根据仿真寻找出串联补偿电容的最优值，其结果如表3所示。

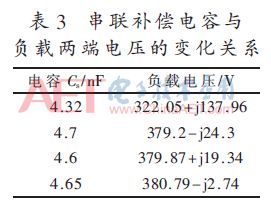
由表3可知，接收回路中串联补偿电容的大小近似为4.65 nF，而实验中串联补偿电容选为4.7 nF，因此仿真中选用接收回路的串联补偿电容为4.7 nF。

3.2.1 接收线圈相对于发射线圈沿水平方向运动

下面仿真耦合机构2的接收线圈沿水平方向运动时ICPT系统的平稳性情况。记发射线圈的中心位置为原点O，以接收线圈在水平方向上的运动轨迹定为x轴，分别对接收线圈的中心位于x=±105 cm、±75 cm、±45 cm、±15 cm这8个位置仿真，得到耦合机构2系统的传输功率随水平位置的变化曲线如图8所示，其中系统的传输功率的相对变化量在2%之内。

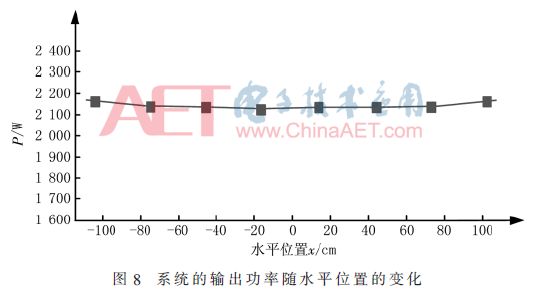
3.2.2 接收线圈相对发射线圈在竖直方向上有偏离

接收线圈相对于发射线圈在竖直方向上有偏离的情况下，仿真耦合机构2系统的传输功率的变化情况。其相对偏离量是在接收线圈的自身高度±10%内，图9是其传输功率随偏离量的变化曲线，其中传输功率相对于无偏离时最大的相对变化量均不大于5%。

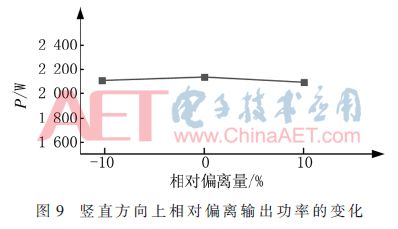
3.2.3 接收线圈在发射线圈内前后侧方向上有偏离

接收线圈在发射线圈内前后侧有偏离的情况下，仿真系统的传输功率的变化情况。其相对偏离量是耦合线圈之间空隙的±20%内，图10是其传输功率随偏离量的变化曲线。其中系统的传输功率相对于无偏离时的相对变化量均不大于2%。

从图8～图10的仿真结果可知，耦合机构2沿轨道相对运动时，ICPT系统传输功率的波动范围均在5%之内，说明这种耦合机构在传输电能的过程中能够保持良好的平稳性。

4 实验结果

4.1 耦合线圈中自感和互感的测量

图11是实验中搭建的两种耦合机构的实验平台，左图是耦合机构1实验装置，右图是耦合机构2实验装置。在接收线圈处于发射线圈的中间位置，实验测得这两种耦合机构的自感和互感如表4所示。

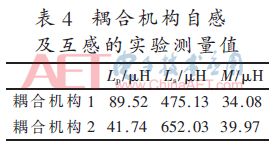
将表2中的仿真值与表4中的实验值对比，根据误差计算公式：误差=

4.2 耦合机构2沿轨道水平运动时测互感的实验

当接收线圈沿轨道水平运动时，利用PA2000mini功率测试仪对ICPT系统进行测试。按照3.2.1小节中8个位置的传输功率进行测量，得到的结果如图12所示，其中传输功率的最大波动在6%之内。图13是接收线圈运动到某一位置时的测量结果，图中星号标记点处系统的输出功率为2.073 kW。

实验结果表明，由实验测量到的数据与仿真数据存在一定的误差，但数据相差不大，并且变化趋势基本保持一致，主要原因是在仿真过程中，耦合结构的建模采用了简化的模型。

5 结论

借用ANSYS电磁场仿真软件分析了耦合机构沿轨道相对运动时，ICPT系统能够保持良好的平稳性，并通过实验验证了该结论。通过理论分析和实验分析发现，工字钢对耦合线圈的自感确实存在一定的影响，使得在接收回路中串联补偿电容的理论计算值和实验值存在一定的差异，而利用ANSYS电磁场仿真软件能够很好地解决这一问题。