1985年,德国鲁尔大学教授Depenbrock和日本学者Takahashi提出了直接转矩控制理论,由于它直接控制定子磁链空间向量和电磁转矩,使得控制系统得以简化,并且提高了快速相应能力。直接转矩控制不仅拓宽了向量控制理论,同时促进了电机现代控制技术的进一步发展。
SIMUUNK是MATLAB提供用来对动态系统进行建模、仿真、分析的软件包。SIMULINK包含许多模块库,利用这些模块库可以很方便的进行复杂系统构建与仿真分析,为研究者提供了一个实用的仿真平台。本文对基于MATLAB/SIMULINK异步电动机的直接转矩控制离散系统仿真模型做出分析和介绍。
1 异步电机的数学模型
1.1 三相变两相的物理意义

1.2 三相异步电机在α-β静止坐标系下的电压、磁链方程:
电机电压方程为:
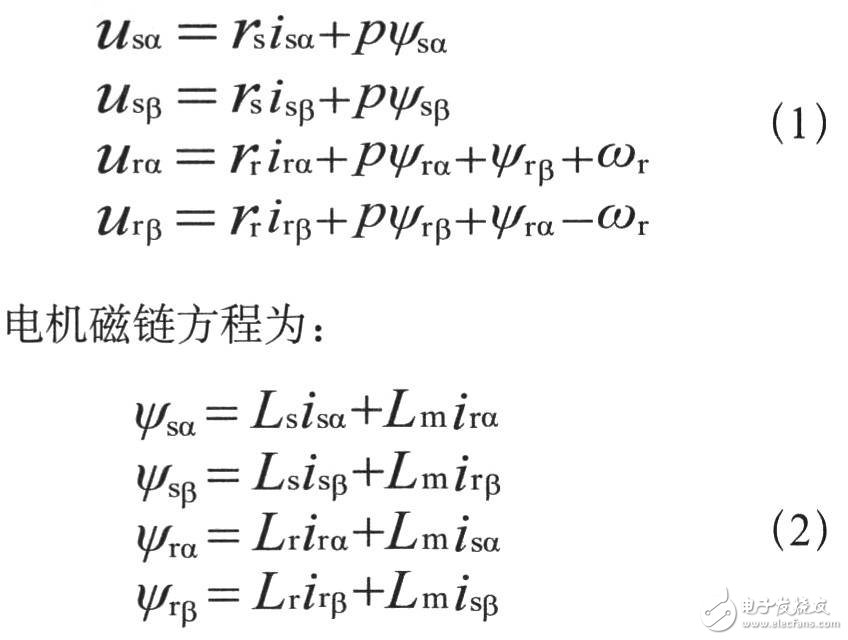
则电压方程的矩阵形式为:
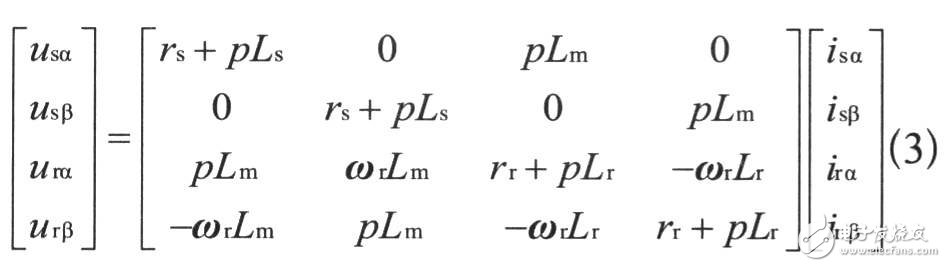
式中usα、usβ、isα、isβ分别是定子在α、β轴上电压、电流分量;urα、urβ、irα、irβ分别是转子在α、β轴上的电压、电流分量;ψsα、ψsβ、ψrα、ψrβ分别是定子、转子在α、β轴的磁链;Ls、Lr、Lm分别是定子绕组、转子绕组及电机励磁电感;P为微分算子;ωr是转子的角速度。
1.3 电机的转矩方程
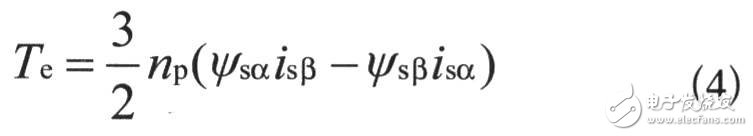
Te为电机的电磁转矩;np为电机的极对数。
1.4 电机的运动方程
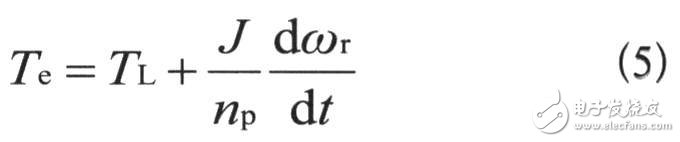
TL为负载转矩;J为电机转子和系统的转动惯量。
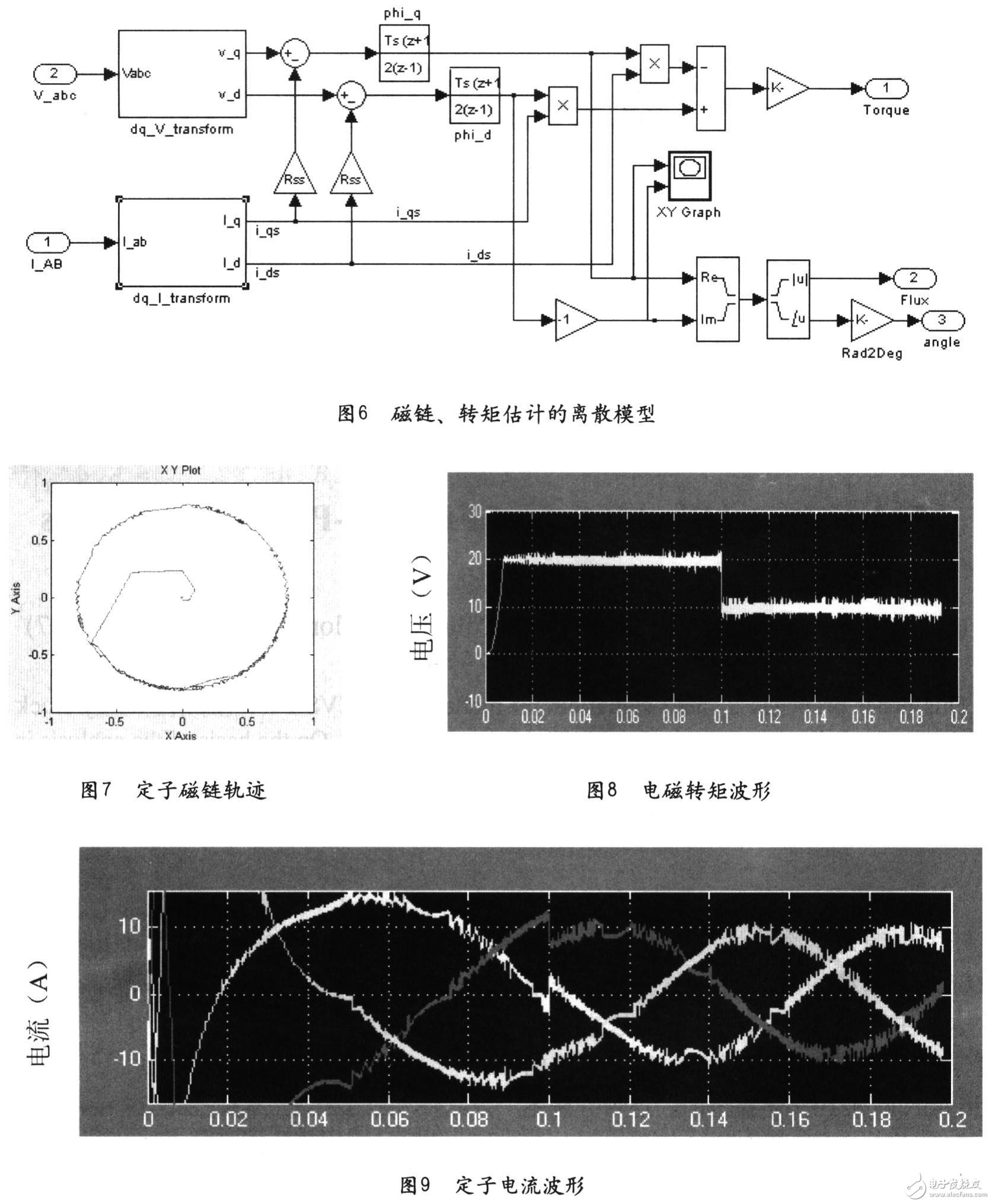
根据异步电机的数学模型,利用SIMULINK的基本模块及电机模块搭建异步电机的仿真模型。
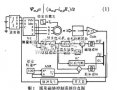
2 建立仿真模型
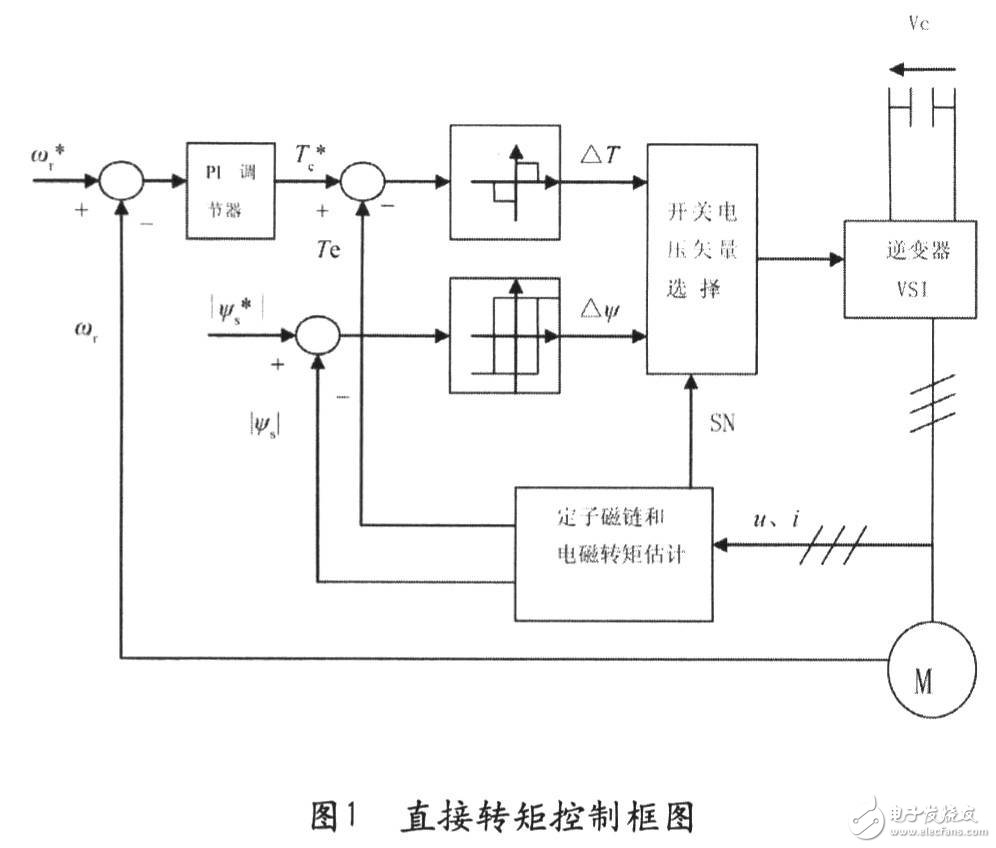
2.1 直接转矩控制基本原理
定子、转子磁链以及电磁转矩可表示为:
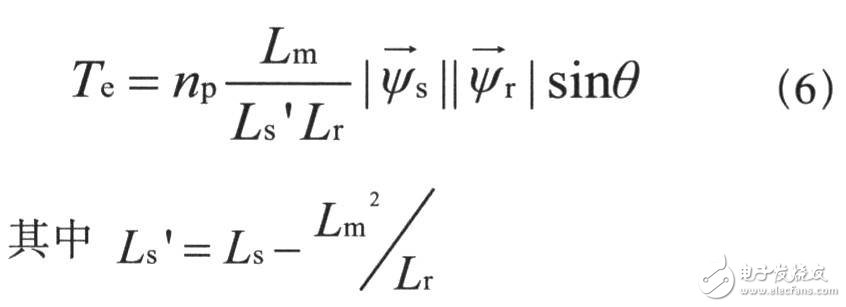
2.2 开关电压矢量的合理选择
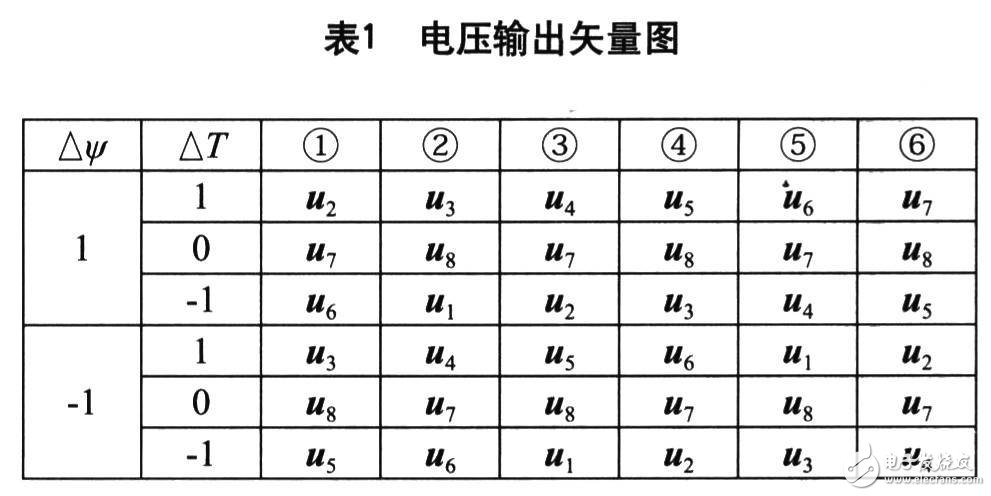
逆变器不同的开关状态可产生如图2中所示的u1~u6及u7,u8两个零矢量。基于便于控制的考虑,把定子磁链所在空间位置划分为①~⑥区间,总共六个扇区。
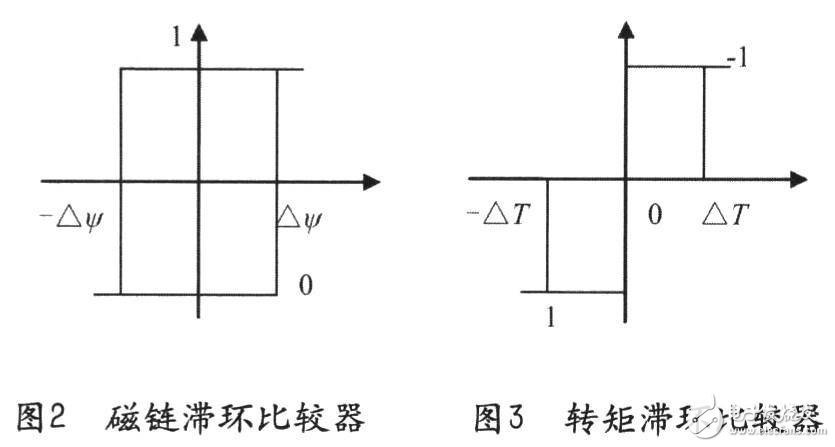
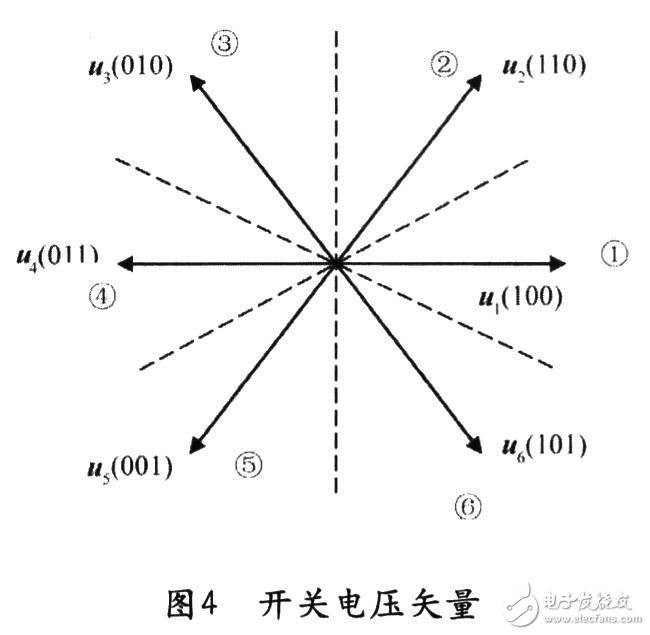
其中△ψ、△T的取值是根据滞环比较器的输出来确定,即有:若|ψs|≤|ψsref|-|△ψs|,则△ψ=l;若|ψs|≥|ψsref|—|△ψs|,则△ψ=一1;若|Tc|≤|Tcref|—|△Te|,则△T=1;若|Tc|≥Tcref,则△T=0,若|Tc|≥|Tcref|-|△Tc|,则△T=一1;若|Tc|≤Tcref,则△T=0。依据图4的磁链区间划分、推理和控制经验得到在磁链所在的区间的电压输出矢量表。
2.3 磁链观测的离散仿真模型
磁链观测采用定子磁链的u一i模型:
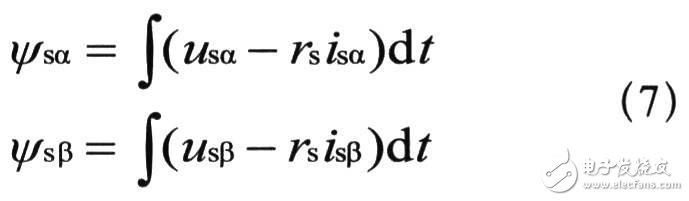
为了验证离散直接转矩控制的可行性,模型采用信号离散采样的方式,将电压、电流离散化,通过离散积分进行磁链观测。

离散定子磁链观测原理如下:
把定子电流、电压和磁链离散化,式(7)可写成下面的离散形式:

基于上面的推导就可以将通常的连续积分改为离散信号的积分,通过改变采样时间Ts来对磁链和转矩的估计精度进行调整。
3 仿真结果
设置电机的仿真参数,额定电压380V,额定功率为2.5kW,极对数np=2,rs=0.435Ω,rr=0.816Ω,Ls=0.006H,Lm=0.08931H,Lr=0.006H,转动惯量J=0.089kg.m2,转矩滞环宽度为lN.m,磁链滞环宽度为0.02wb。
4 结论
本文通过MaUab/simulink搭建出直接转矩控制离散仿真系统,并进行仿真研究,得出定子磁链、转矩、定子电流的波形(见图7~图9)。从仿真结果来看,图7的定子磁链轨迹近似为圆形,图9的定子电流近似为正弦波形,从而验证了此离散模型的正确性。直接转矩控制离散仿真系统为直接转矩控制系统仿真提供了一种新思路,是一种有益的探索。
-
matlab
+关注
关注
185文章
2974浏览量
230452 -
电动机
+关注
关注
74文章
4110浏览量
96280 -
仿真
+关注
关注
50文章
4080浏览量
133586
发布评论请先 登录
相关推荐
三相异步电动机直接转矩控制系统的matlab/simulink设计实现
永磁同步电机直接转矩控制系统中的MATLAB/Simulink建模方法
基于Matlab/Simulink建立在直接转距控制系统中的定子磁链仿真模型
三相异步电动机直接转矩控制系统的matlab/simulink实现





 基于MATLAB/simulink的直接转矩控制离散仿真系统的研究分析
基于MATLAB/simulink的直接转矩控制离散仿真系统的研究分析










评论