本论文结合上述情况,在某项目中总结出了一套对PID算法的参数进行整定的方法。PID调节方法是三阶系统中一种常用的有效控制方法。PID在许多系统中能够得到广泛的运用是由于这些系统都存在非线性和未知的干扰,尤其是在模拟和数字的混合系统中,由于模拟信号很容易受到影响,导致系统设计较为复杂。在一些相互合作的项目中,由于存在单位之间需要保密的原因,对系统的理论分析通常不能够做到具有精确的数学模型,因此,PID算法是解决这类情况的一种有效控制方法。
1 传统数字PID算法
1.1 位置式控制算法
位置式PID控制算法描述为:

式中:k——采样序号;
u(k)——第k次采样时刻的计算结果;
e(k)——第是次采样相对目标位置的偏差值;
Kl——积分系数;
KD——微分系数;
KP—— 比例系数;
TI——积分时间常数;
TD——微分时间常数;
T——采样周期。
由式(2)可以看出,每次输出与过去的状态有关,要想计算u(k),不仅涉及到e(k-1),且须将历次相加。故用式(2)计算复杂,浪费内存。控制从手动切换到自动时,必须先将计算机的输出值设置为原始阀门开度uD,才能保证无冲击切换。
1.2 增量式控制算法
增量式PID控制算法描述为:
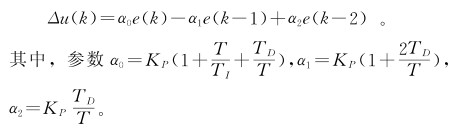
增量式只需计算增量,当存在计算误差或精度不足时,对控制量计算的影响较小。由于算式中不出现uO,易于实现手动到自动的无冲击切换。此外,在计算机发生故障时,由于执行装置本身有寄存作用,故可仍然保持在原位。
基于以上两种常规的算法,我们在实际应用中又提出了多种改良的算法。在本项目中采用了积分分离PID控制算法。
2 积分分离PID算法
积分分离控制算法的数学模型如下:
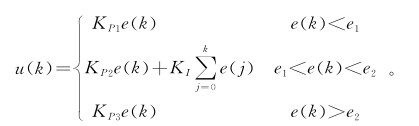
其中,e1、e2分别表示左、右的区间,即离目标位置的距离,这是常规积分分离PID控制算法。在实际的应用中可以根据不同的系统和实际情况再度进行分段。
3 位置伺服系统中的算法
在我们研究的系统中,所用的方法是多次积分分离以及在正反向超调的过程中进行的积分分离。
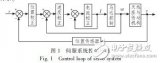
首先我们对所用的参数整定数学模型进行一下描述,其中的分段见图1。
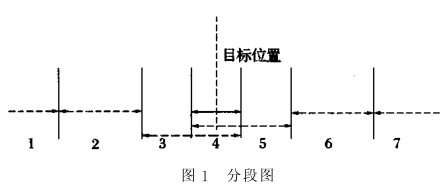
图1中,1和7表示在全速运动区间有正、负之分。以右为正,左为负;2和6分别表示在目标位置的左、右利用纯比例调节控制的区间;3和5分别表示需要利用常规PID算法的部分;4表示在小误差范围内利用比例积分控制。
上述分段是针对实际系统进行的分段,是适合这个系统的一个分段方法,它不仅在速度和精度上都可以满足要求,而且比我们所用过的其它方法都更加适合这个系统。
4 参数整定
由于我们研究的这个系统是一个位置精度要求比较高的系统,所以对参数的整定要求比较高,在不断实验的基础上总结出了一套适合本系统的通过近似计算得到参数的方法。
由于本系统是一个随动系统,建立系统精确的数学模型比较困难,只知道前向通道的放大倍数是N,电机饱和电压是U1以及电机的最大速度是v1。位置环参数的整定影响整个系统的精度和快速性,我们在不断实验的基础上,总结出如下方法:
(1)对系统进行相应的分段。分段是根据实验确定的,由于系统本身是复杂的非线性的高阶系统,所以分段是一个比较重要的环节,通过实验不断测试系统在不同情况下的阶跃响应,将其作为分段依据。
(2)确定最后算法部分的参数。我们对不同的位置采用不同的PID算法,其中转折部分的电压是一个比较关键的参数,根据实验,我们确定将通过算法输出的电压乘以前向通路的放大倍数作为加载到电机上的电压值,当然这个电压值必须使得电机在负载情况下还有速度。
(3)确定2段、6段的比例系数。这里的比例系数是通过两个转折点的电压和位移量来得到的,是一个线性的函数关系,即U输出=KPS位移。其中,U输出是算法输出部分;KP是2段、6段的比例系数;S位移是相对于目标位置的位移量。通过1和2或6和7之间的转折部分可以得到一组U输出、S位移,并通过2和3或5和6之间的转折部分又可以得到另一组U输出、S位移,从而确定KP。
(4)确定第4段的PID参数。通过以上得到的转折部分的电压值,我们有了起始电压,再根据得到的起始电压,就可以确定比例系数。确定这个比例系数时,必须使得积分和微分系数为0。通过这个比例系数的确定,我们就可以完全地通过计算得到所需要的参数。为满足精度的要求,根据经验加入适当的积分项就可以完成参数的整定。注意这里积分项加的越小越好,当然要在保证精度的范围内。
5 结 论
通过实验证明我们所得到的运动过程满足了快速性和精度的要求。在实验中总结出的方案是可行的,也是合理的。
-
计算机
+关注
关注
19文章
7519浏览量
88204 -
PID
+关注
关注
35文章
1472浏览量
85609 -
伺服系统
+关注
关注
14文章
575浏览量
39248
发布评论请先 登录
相关推荐
PSO算法在数控机床交流伺服系统PID参数优化中的应用
基于Simulink环境下的船载雷达伺服系统PID参数整定




 对某位置伺服系统中PID算法参数进行整定的方法研究
对某位置伺服系统中PID算法参数进行整定的方法研究
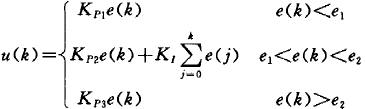











评论