自抗扰控制技术在非圆数控车削中的应用研究及设计

为了提高非圆车削中快速伺服刀架的跟踪精度和抗干扰性，研制了一种自抗扰控制器。通过对执行机构建模分析，将模型中的非线性部分归结为系统的内扰，将加工过程中切削力干扰归结为系统外扰，设计出相应的扩张状态观测器，对系统内、外扰的总和做出实时估计和补偿。仿真实验表明，自抗扰控制性能优于传统的PID控制。通过DSP（digital signal processor）编程，将自抗扰控制器应用于非圆车削。切削加工试验结果表明，自抗扰控制具有良好的控制品质，快速伺服刀架跟踪精度控制在5μm以内。

非圆数控车削是实现非圆截面零件高效、柔性、高精度加工的有效方法。非圆车削时，刀具在快速伺服刀架（fast tool servo，FTS）的驱动下，随着主轴高速回转沿工件径向做快速往复运动。FTS的跟踪精度是影响非圆截面零件轮廓精度的主要因素。FTS控制器设计面临两个技术难点：第一，如何提高FTS的伺服刚度，以减小变化的切削力对跟踪精度的影响；第二，如何减小FTS执行机构的非线性和参数变化对跟踪精度的影响。

目前，许多学者都对适于非圆车削的FTS控制器进行了深入研究。文采用PID控制结合前馈补偿的方式，设计出基于位置反馈和速度反馈的两种干扰观测器。文针对非圆车削中，跟踪信号为有规律的周期信号这一特点，采用重复控制算法，并进行了相应的改进，增强了系统响应的快速性。文采用模型参考自适应控制，对FTS进行控制，提高了系统的鲁棒性和抗干扰能力。

自抗扰控制（active disturbance rejectioncontroller，ADRC）是一种基于误差反馈的非线性控制方法，其原理简单，可对系统的未建模动态和未知扰动做出很好的估计和补偿，具有很强的适应性和鲁棒性。本文应用自抗扰控制技术，根据非圆车削对FTS控制器在跟踪精度、响应速度、抗扰动性等方面的要求，研制了自抗扰精密跟踪运动控制器，并进行仿真分析和切削试验。

1 被控对象建模

非圆车削采用的FTS执行机构结构见文，它采用音圈电机驱动原理，弹簧和滚动导轨复合支承，可近似为弹簧阻尼系统，运动微分方程为

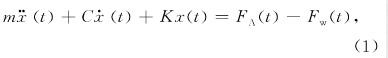
其中：m为运动部分质量，K为执行机构内弹簧的刚度系数，C为阻尼因数，Fw为加工过程中的切削力，FA为电磁力。根据电磁力汁算公式，有FA（t）=nBLI（t），其中：n为线圈匝数，B为磁通密度，L为有效线圈长度，I为电流强度。

对执行机构进行控制时，输入为电压控制信号，通过功率放大器转换为电流输出，转换的关系为I（t）=ku（t），运动方程可写为如下形式：

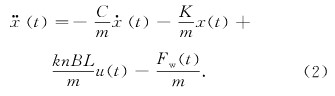
然而，执行机构在实际工作过程中，由于线圈磁通不均匀和磁阻推力，使得执行机构的推力与线圈电流并不呈线性关系，从而给控制带来了较大的难度。同时，由于切削力在加工过程中是实时变化的，也对系统的稳定性产生了很大的影响。

2 自抗扰精密跟踪运动控制器的设计

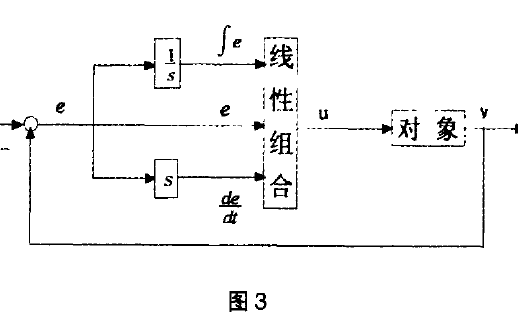
图1给出了自抗扰控制器结构。

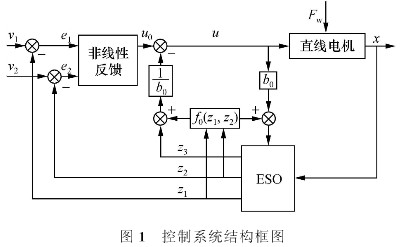
典型的自抗扰控制器包括跟踪微分器（trackingdifferential，TD）、扩张状态观测器（extended stateobserveF，ESO）和非线性反馈控制器3部分。n阶TD的作用是给出不可微输入信号的跟踪信号及其l至n-l阶微分信号。TD产生的信号相对于输入信号有少许滞后，此外，非圆零件截面形状一般用可微函数表示，直接对该函数求导就可以获得参考信号的微分值。因此，本控制器去掉了TD环节。。ESO可实时估测出被控对象的各阶状态变量和系统的总扰动中的未知部分（包括内扰和外扰），并给予补偿。非线性反馈控制器将TD的输出信号与由ESO观测到的相对应的状态变量作差后，经过非线性组合，产生未包含扰动在内的控制量，达到提高系统的快速性，减小超调量的目的。

设FTS执行机构在实际工作过程中，推力FA与输入u之比为一未知函数b（t）。则执行机构的运动微分方程可写为：

3 仿真分析

为了考察自抗扰控制器抵抗外界扰动和内部参数变化的能力，利用Matlab编程，分别进行了仿真分析。为了更直观地说明问题，同时还对PID控制进行了仿真。在仿真编程时，被控对象采用二阶模型。由于实际被控对象中的未建模环节，在比例系数过大时将造成系统不稳定。为了尽量准确地反映实际加工过程中切削力的影响，仿真过程中对两种控制算法的比例系数根据实际情况进行了限制。在此限制下，通过反复调节，分别整定出使跟踪误差最小的控制参数，并用这组参数进行了下面的仿真实验。

3．1 抵抗外界扰动的性能分析

非圆车削中FTS所受到的外界扰动主要是变化的切削力，故仿真分析时干扰信号采用加工过程中两种典型的切削力信号。仿真采用的参考信号为非圆车削过程中刀具沿工件径向理想的往复运动轨迹。以主轴转速1 200 r／min，加工椭圆度为0．4 mm的活塞为例，刀具运动方程为y=100（cos（251．33t／s）-1）。

试验1：从第0．05 s开始，加入幅值为50 N，频率与刀具运动频率相同的切削力信号Fw／N=50（1-cos（251．33t／s）），这相当于由圆形截面车削形成非圆截面的工况。仿真结果如图2所示，其中纵坐标为跟踪误差e，横坐标为时间t。

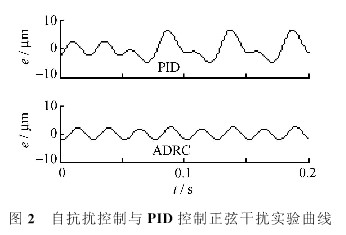
由图2可以看出，PID控制在加入干扰信号后，误差幅度明显增大，误差曲线规律也有明显改变。而自抗扰控制在加入干扰信号后，所受到的影响基本被消除，误差范围与未加入干扰前相当，说明自抗扰控制有良好的抗干扰特性，对于因切深变化而产生的交变切削力，抑扰能力要强于PID控制。

试验2：从第0．05 s开始，加入幅值为50 N，频率与刀具运动频率相同的方波切削力信号，这相当于加工带有活塞削孔椭圆形截面的工况。两种控制方法的跟踪误差仿真结果如图3所示。

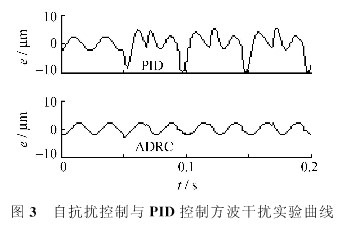
从图3可见，方波切削力干扰信号由于具有力突变的性质，所以对控制系统的影响要大于正、余弦干扰信号。对于自抗扰控制，在切削力发生突变时，误差仅发生小幅波动，对整体的误差范围没有影响。但对于PID控制，这种干扰所带来的误差波动是相当剧烈的。因此，对于因凹槽等原因而产生的方波规律变化的切削力，自抗扰控制的抑扰能力也强于PID控制。

3．2 抵抗内部参数变化的性能分析

为了检验控制算法抵抗内部参数变化的能力，在上述参考信号的基础上，从O．05 s开始，将FTS执行机构的输出增益减小50％，试验结果如图4所示。

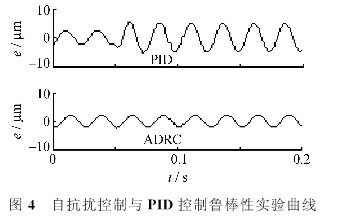
从图4可见，增益减小50％后，PID控制的误差范围有了较为明显的变化，而自抗扰控制的跟踪效果几乎没有受到任何影响。这个试验充分反映了自抗扰控制对被控对象模型不依赖的特性，其鲁棒性强于PID控制。

4 切削试验研究

4．1 试验系统

切削试验是在G-CNCP200型中凸变椭圆活塞数控机床上进行的。该机床横向和纵向运动为开环控制，交流伺服驱动。FTS机械结构部分安装在机床的横向刀架上，驱动刀具实现精密往复运动。主轴采用变频控制，可实现无级调速。FTS硬件包括DSP（digital signal processor）控制板，D／A转换器，功率放大器和线性执行机构和线性光栅5部分。DSP控制器经过算法运算后，通过数摸转换器将模拟控制信号发送给功率放大器，经放大后直接驱动机构往复运动，其位置值通过尾部的光栅反馈回DSP控制板，形成一个闭环控制系统。

DSP控制板采用TMS320LS2407型DSP芯片。这种芯片主频为30 MHz，支持32位加法及1616位乘法运算，并同时支持汇编语言和C语言编程。由于加工过程中采样周期仅几十微秒，为了尽量缩短控制周期，同时方便优化程序代码，本文采用汇编语言编程。由于该DSP控制板为定点DSF，所以在进行浮点运算时，需要事先进行定标处理。同时，由于定点DSP在执行开方等指数运算时，执行效率较低，所以在编写程序时，考虑将算法中的非线性函数做线性处理，以简化程序，缩短控制周期。通过仿真实验，简化处理后，控制周期可缩短50％以上，而快速性略有下降，但对抗干扰性和鲁棒性影响甚微，所以采用线性处理是必要且可行的。

4．2 切削试验

切削试验所用活塞试件材料为硬铝（2A80），椭圆度分别为0．2、0．4、0．6、0．8mm，刀具材料为硬质合金（YT3）。分别在主轴转速800、l 000、1 200、1 400 r/min，切削深度0．05、0．1、0．2、0．3mm，进给量0．05、0．1 mm／r条件下，进行了多次正交切削试验。

上述各种切削试验中刀具跟踪运动误差控制在5μm以内。图5给出了主轴转速1 200 r／min，进给量0．05 mm/r，切深分别为0．05、0．1和0．2mm时刀具跟踪运动误差。在实验过程中发现，跟踪误差随切削深度的增加而略有增加，但所加工活塞的椭圆度对误差范围的影响很小，因此，在加工大椭圆度活塞时将获得很好的相对误差值。

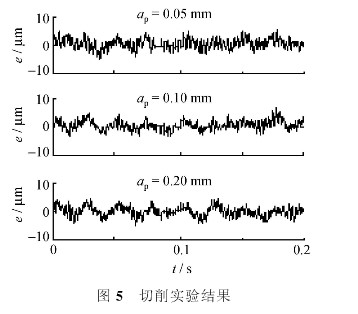
切削试验结果表明，所设计的自抗扰精密跟踪控制器能抵抗非线性变化的切削力的影响，跟踪精度能满足加工要求。但是，与仿真分析结果不同，切削时刀具跟踪运动的误差曲线包含许多毛刺，这是由于光栅反馈分辨率为0．5／μm，从而造成误差曲线跳变，同时也影响了跟踪精度；此外，DSP的定点运算功能限制了参数的取值和运算精度，从而也降低了跟踪控制精度。

5 结 论

本文将自抗扰控制技术应用于非圆数控车削中的快速伺服刀架控制。通过对执行机构建模和分析，设计出自抗扰控制器。在Matlab仿真试验中，自抗扰控制在抗干扰性与鲁棒性上，均优于传统的PID控制方法。活塞切削实验结果表明，应用该控制算法，加工精度可达5／μm。目前，中国的数控非圆车削机床，加工精度一般在1 0 μm左右，国外进口机床加工精度虽然可达5μm以内，但价格昂贵。因此，本文进行的此项研究，将具有很大的应用价值。