如何使用了一个简单的反证法，就证明了159年来无人能攻克的黎曼猜想

40分钟后，89岁的阿蒂亚爵士（Sir Michael Francis Atiyah）完成了他全球瞩目的黎曼猜想证明演讲，现场听众报以10多秒的掌声。

接下来是提问环节。

没想到，高智商听众云集的会场里，随即陷入一片沉默。“Come on！”等待20秒仍不见人提问的阿蒂亚呼吁大家勇敢一点。

直到一分钟后，站在台上的阿蒂亚才听到第一个问题：

“黎曼猜想这算是被成功证明了吗？”

提问者应该是一位印度小哥，他来自数学家鄙视链的下下游，人工智能领域，一上来就抛出这个尖锐的问题。

阿蒂亚说，他自己觉得算是已经证明了黎曼猜想，不过如果你坚决不接受反证法的话……

当然，阿蒂亚也表示这个证明现在还不完整，接下来还有很多后续问题要解，今天只是万里长征的第一步，不过，第一步也应该算是问题的一个解。

他说：“我可以退休了。”

第二位提问观众关心论文什么时候发表，好检验一下这个证明。这样一个问题勾起了阿蒂亚的伤心事。

顺着这个提问，阿蒂亚开始吐槽了学术界的“老龄歧视”。他说：“等你到了我这个年纪，人们就不发表你的论文了，他们会说你太老了，肯定哪儿证明错了。”

他说他甚至被arXiv拒了稿，简直是歧视啊。

第三位提问的终于是个小姐姐，关心了一下阿蒂亚自己对证明黎曼猜想这件事的感受：你认为大家会相信你的证明吗？还是说你根本不在乎大家信不信？

大家信不信，阿蒂亚是很在乎的。他说，得不得奖不重要，有人听才重要。

不过，大家不信也正常，因为他发现，如果有人给旧方法找了种更聪明的用法，人们还比较容易相信，但大家不愿意相信全新的证明。

而他这次所讲的，就是一个全新的方法。

核心三分钟

作为菲尔兹奖与阿贝尔奖双料得主、英国皇家学会院士，阿蒂亚爵士于德国柏林时间9月24日上午9点45分登上讲台。

在他40分钟的演讲中，大部分在回顾历史，严格来讲，只有三分多钟在讲解他如何使用了一个简单的反证法，就证明了159年来无人能攻克的黎曼猜想。

三分多钟讲解，只有一张PPT。

阿蒂亚爵士对黎曼猜想的证明，只是推演物理学中精细结构常数α的副产品，建立在冯·诺依曼（John von Neumann）和弗里德里希·希策布鲁赫（Friedrich Hirzebruch）工作的基础之上。

也就是说，他最初也不是想根据这两位的工作来证明黎曼猜想，而是要推演精细结构常数。

精细结构常数通常被认为约等于1/137.03599913，但它究竟是怎么来的，到底是不是一个常数，困扰着无数物理学家，就像黎曼猜想困扰着数学家一样。

这个推演过程，就用上了Todd函数，这个函数是希策布鲁赫用阿蒂亚老师的名字命名的。

阿蒂亚在推演精细结构常数的过程中，发现Todd函数还能用来证明黎曼猜想，于是就有了今天这场演讲。

用Todd函数，靠反证法证明黎曼猜想的过程，全在下面这一页PPT里了：

为了避免曲解（实际也听不懂）阿蒂亚的原意，我们把现场这段三分多钟的讲解，剪出来放在这里，我们一起聆听大师现场教学：

想要进一步研究，可以参考阿蒂亚证明黎曼猜想的论文预印本。

论文获取链接:https://pan.baidu.com/s/1m6de_9f2503yZeyQPqlwvA提取码: cs2u

全文很短，只有5页。

同行不予置评

不知道这个证明，你能看懂几分。

但根据我们的观察，这个演讲发表之后，阿蒂亚爵士并没有收到太多的赞美。科技媒体New Scientist曾经联系了多位数学家，问他们怎么看阿蒂亚证明黎曼猜想的方法，但数学家们大多表示不予置评。

就像爵士演讲之后的提问环节，全场无人举手，空气像冻住了一样。

△“证明部分，就留作课后练习吧。“

从20日发布演讲预告，到昨天下午演讲结束，外界对阿蒂亚的这份证明，一直不太看好。毕竟十年来，他几乎没有做出过让学界认可的成果了。

甚至，演讲开始前传出的预印本，许多人都怀疑是假的，不相信阿蒂亚会给出那样的证明。听了演讲之后，才惊呼“啊，是真的啊。”

另外，阿蒂亚爵士在演讲中提到，证明过程中用到的最重要的工具，是Todd函数。

针对这一点，有不止一个网友表示，“这跟Todd函数没啥关系啊，就是多项式而已。”

另外据《文汇报》报道，对于阿蒂亚这次的工作，有同行在网上表示，为了尊重这位曾经做出过非常杰出而漂亮工作的伟大数学家，就不要再讨论了，因为他的证明是“not even wrong”。

在科学界，这个英语短语描述了一个声称是科学的论点或解释，但是基于无效的推理或推测前提。因此，它指的是不能严格地、科学地讨论的论述。

再看看学术讨论之外的世界，推特用户的娱乐精神就比较充足：

“我跟导师聊起阿蒂亚证明黎曼假说的事。他说每个人，不管 (前一秒) 是在带孩子，还是在呼吸，还是在干嘛，都纷纷放下手上的事，开始证明黎曼假说了。”

妄自解读了一下这条评论，大概是说，这样就能证明的话，是人都能证明了。

当然，负面评价也不是全部。

有人指出，这份证明，只是阿蒂亚其他研究的一个推论(Corollary) ，而那些研究外界都没有看过，无从评价对错。真正的问题在于，Todd函数到底是怎么用的。

阿蒂亚本人也说，这个证明只是“万里长征第一步 (the First Step on a Long Road) ”，还有很多需要补充的东西。

不过，他依然相信，自己有理由把 (证明黎曼猜想的) 100万美元收入囊中。

全程视频+PPT

阿蒂亚此次演讲+问答的全程，视频在此：

如果你想下载观摩阿蒂亚此次演讲使用的PPT，这里是下载地址：https://pan.baidu.com/s/1akir2ySSlHbU4lxyYfI9CA（提取码: qeb7）

黎曼猜想简史

所以讲了这么多，黎曼到底猜想了啥？

一个找质数的方法。

质数，就是自然数中那些只能被1和它自己整除的整数。比如2、3、5、7、11、13、17、19、23……这些数。

质数看起来似乎没什么规律，在数轴上突然地出现，又突然地消失，从古希腊开始，人们就被这个“玄学”所困扰：

质数啊，你们到底有没有什么规律？

然而当时，古希腊人对质数除了定义之外的唯一知识就是：

自然界有无数个质数。

这个证明来自于欧几里得，他用反证法证明了这一点。

之后的1600年，人们对于素数的认知毫无进展。

研究调和级数的奥里斯姆大佬

时间一跃来到了中古晚期，法国瓦卢瓦王朝国王查理五世的顾问，title包括经济学家、数学家、物理学家、天文学家、哲学家、音乐学家、神学家等一长串的一位大佬尼克尔·奥里斯姆（Nicole Oresme）研究出了一个新的函数：调和级数发散

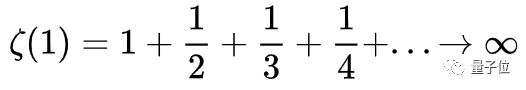
是不是觉得看起来很玄学？

他的证明过程就很简单了，非常的奥数style。

△调和级数发散的证明，小学数学就能看懂

调和级数发散看起来跟质数似乎没啥关系，但是就是这个式子，一不小心给后来的黎曼猜想奠定了基础。

欧拉老师的乘积公式

奥里斯姆大佬告别历史舞台353年之后，轮到欧拉老师秀了。

莱昂哈德·欧拉（Leonhard Eule），就是那个从陪伴大家从中学到高数到复变函数的欧拉老师，他发现了一个名叫欧拉乘积公式的函数：

这个公式仿佛冥冥中和质数的分布有某种联系，数学王子高斯（Gauss）和另一位数学大师勒让德（Legendre）就感觉到了这一点，俩人不约而同的提出了质数定理：

从不大于n的自然数中随机选一个，它是质数的概率大约是1/ln n。

黎曼大神登场

前面四位数学家做了一些铺垫之后，主角黎曼大神终于登上了历史舞台。

黎曼33岁那一年，当上了柏林科学院的通信院士，这可是非常高的荣誉，黎曼一开心，想想来这么好一家单位不能白来，我来的时候以单位为荣，我走的时候就要单位以我为荣。

怎么以我为荣呢？黎曼就写了一篇牛逼哄哄的论文，题目叫《论小于已知数的质数的个数》，翻译成人话就是：质数是怎么分布的。

这篇论文里，黎曼提出了一个函数，被后世称为黎曼ζ函数（ζ，读音Zeta）。

如果把它展开，你就会发现，黎曼ζ函数长得跟前面奥里斯姆调和级数发的式子差不多。

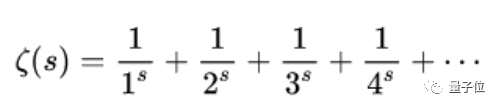
之后，黎曼还定义了两类零点：

平凡零点：某个三角sin函数的周期零点；

非平凡零点：ζ函数自身的零点。

针对非平凡零点，黎曼提出了三个命题：

第一个命题，黎曼指出了非平凡零点的个数，且十分肯定其分布在实部大于0但是小于1的带状区域上。

黎曼大神形容“这是不言而喻的普适性的结果”，意思就是“这特么简直是废话，还用说吗？”

可是地球上的其他人类不这么觉得。46年后，在芬兰数学家梅林和德国数学家蒙戈尔特的努力下，第一个命题终于被证明了。

第二个命题，黎曼提出所有非平凡零点都几乎全部位于实部等于1/2的直线上。

这个命题，黎曼大神自己证出来了，可是他不说，因为他觉得命题的证明还没有简化到可以发表的程度。

这些地球上的其他数学家懵逼了：大神你不说就撒手西去了，这得让我们活着的数学家急死啊！

所以这个黎曼觉得很简单的命题，地球上的其他数学家至今还处在一脸懵逼的状态中。

第三个命题，黎曼不像前两个那么确定了，他用十分谨慎的语气写到：很可能所有非平凡零点都全部位于实部等于1/2的直线上。这条线，从此被称为临界线。

注意，黎曼猜想终于出现了！就是这第三个命题。

从此，黎曼猜想就开始折磨数学家们：到底能不能证明？能证明还是证伪？什么时候才能证明？

数学家们纠结到什么程度呢？

如果能穿越到500年后，德国数学家希尔伯特醒来的第一句话就是：黎曼猜想被证明还是证伪了？

美国数学家蒙哥马利也说，如果有魔鬼答应让数学家们用自己的灵魂来换取一个数学命题的证明，多数数学家想要换取的将会是黎曼猜想的证明。

黎曼猜想，简直是数学界の终极奥义。

后世数学家的烧脑历史

虽然黎曼猜想很难证明，不过别忘了前面的第二个命题，他自己证明了，还不说，黎曼大神可是一个喜欢藏着掖着的人啊！

于是后世数学家们就开始扒拉黎曼遗留的手稿。

万万没想到，黎曼大神自己谨慎到证明没简化就不发，可是黎曼大神的管家是个粗心汉。他想都没想，就把主子遗留的手稿给烧了。

不过，好歹黎曼的遗孀是个聪明人，她看管家犯傻，就赶紧去抢救了一部分手稿出来，送给了黎曼生前好友、另一位数学家戴德金。

可是送过去之后，黎曼夫人后悔了：万一那些手稿里有黎曼给我写的情书呢？

她就找戴德金把大部分手稿要回来了，剩下的被戴德金献给了哥根廷大学图书馆。

因为天才的思路普通人往往跟不上，这些手稿看起来很难懂。不过，关于手稿的故事我们告一段落，后面它会发挥巨大的价值。

下面，则是历代数学家们一步步靠近黎曼猜想真理的过程。

阿达马与普森

黎曼去世30年后，法国数学家雅克·阿达马和英国天文学家诺曼·普森两位也不约而同了一下，他们几乎同时证明了ζ(s)的所有非平凡零点的实部均小于1，即Re(s)=1上无非平凡零点。

所以这也就是素数定理。

玻尔与兰道

时间走到了一战爆发那年。

丹麦数学家哈拉尔德·玻尔和德国数论家爱德蒙·兰道开始了一场合作，证明了玻尔-兰道定理：

含有临界线的任意带状区域都几乎包含了ζ的所有非平凡零点，表明了临界线为零点汇聚的“中心位置”。

零点现世

黎曼一直在讲“零点”。

可是，他要的零点在哪儿？没人知道。

1903年，丹麦数学家第一次算出了前15个非平凡零点的具体数值。在黎曼猜想公布44年后，人们终于看到了零点的模样。

毫无意外的是，这些零点的实部全部都是0.5。

哈代与利特尔伍德

1921年，英国数学家戈弗雷·哈代和约翰·李特尔伍德证明了存在常数T，使临界线上虚部位于0与T之间的非平凡零点的数量至少为KT。

四年后，两人还算出前138个零点，这基本达到了人类计算能力的极限。

沉迷手稿的西格尔

还记得前面的手稿么？终于有人看明白啦！

1932年，德国数学家西格尔（Siegel）在手稿中发现了一个被尘封了73年的公式：

△来自维基百科截图

这个公式表明，黎曼当年发表第三命题不是拍脑门瞎说的，而是经过了深刻的思考和计算。为了纪念西格尔对手稿的辛苦挖掘，这个公司后来被叫做黎曼-西格尔公式。

利用黎曼-西格尔公式，后来的数学家们就可以开心的找零点了。

挪威数学家塞尔伯格（Selberg）证明了临界线上的零点个数占全部非平凡零点个数的比例大于零，这意味着临界线上的零点在全部零点的分布中举足轻重。

之后，美国数学家莱文森（Levinson）引入了独特的方法，证明临界线的零点占全部零点的比例达到了34.74%。

基于莱文森的技巧，美国数学家康瑞（Conrey）在1989年把比例推进到了40%，这也是迄今为止得到的最好结果。