任何一本信号与系统的教材上,都有这样一个结论:
LTI系统稳定性的充要条件是:单位冲激响应h(t)/h(n)绝对可积/绝对可和。但是,理想低通滤波器呢?它是不是稳定系统?如果是,它的单位冲激响应满足绝对可积吗?如果不是,能找到一个有界的输入,通过理想低通,产生无界的输出吗?
下面是厦门理工学院唐骏老师的一篇旧文,此惑一直未解,欢迎大家讨论。
以下试卷摘自《信号与系统学习指导》:
选择题第4题所给的参考答案是B,即说明理想低通滤波器是稳定的,这一点似乎没什么疑问?!
以下摘自《信号与系统》第二版 奥本海姆 刘树棠 译
(6.19)式并非绝对可积,关于这一点,可参考《数字信号处理理论、算法与实现》第二版 胡广书 P96,摘抄如下:
综上可以得出以下两个结论:
1、低通滤波器是稳定的;
2、其单位冲激响应h(t)是平方可积的,但不是绝对可积的。
然而,在几乎所有的信号与系统的教材中都有如下结论:
LTI系统稳定的充要条件是:单位冲激响应绝对可积或单位脉冲响应绝对可和。
以下摘自《信号与系统》第二版奥本海姆 刘树棠 译 P82:
以下摘自《信号与系统性系统分析》第四版吴大正 P339:
通过以上分析,有关LTI系统稳定条件是否应该作修改?还是分析过程中有不对之处?
以上为唐老师原文。我查阅了一下数字信号处理的书籍,对于离散时间系统,也有相同的结论。以下为为程佩青《数字信号处理第四版》清华大学出版社P30页。
下面是书中P96和P97页,阐述了绝对可和与平方可和的区别,也明确指出,理想低通滤波器的单位冲激响应h(n)不满足绝对可和,满足平方可和。但书中未分析其稳定性。
那么,理想低通滤波器,到底是不是稳定系统呢?欢迎大家来讨论。
-
滤波器
+关注
关注
161文章
7811浏览量
178083 -
LTI
+关注
关注
0文章
11浏览量
10484
原文标题:关于LTI系统稳定性充要条件的一个疑问
文章出处:【微信号:SignalAndSystem_DSP,微信公众号:信号与系统和数字信号处理】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
LC低通滤波器作用及应用案例
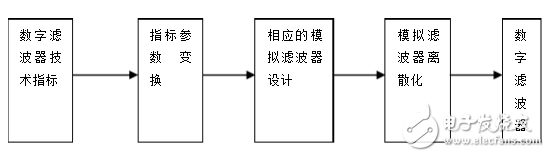
数字低通滤波器的设计

基于MATLAB的理想低通滤波器的设计
LTCC低通滤波器的设计解析
低通滤波器的设计与实现
Matlab低通滤波器设定与实践

低通滤波器与高通滤波器有什么不同
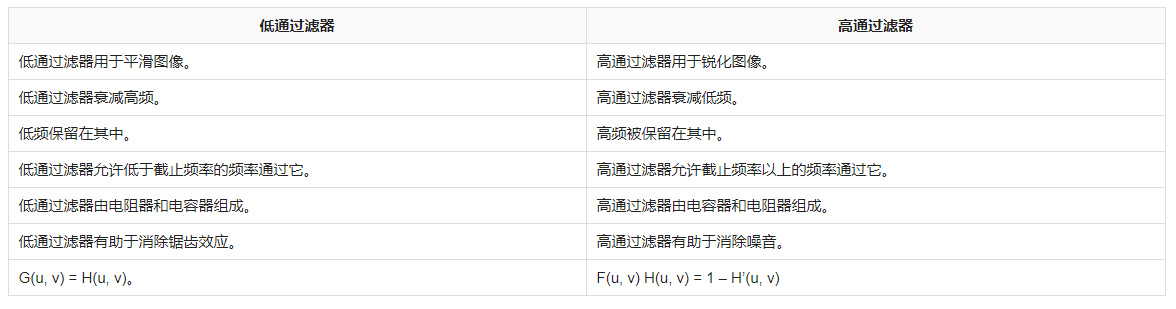
高通滤波器和低通滤波器的关系
低通滤波器电路图分享
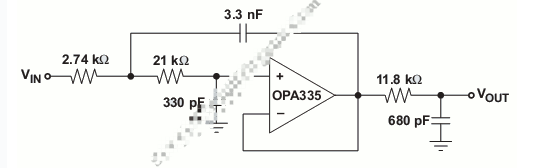




 理想低通滤波器,是稳定系统吗?
理想低通滤波器,是稳定系统吗?












评论