推荐系统中的EE问题及解决问题的基本Bandit算法详细概述

1、推荐系统中的EE问题

Exploration and Exploitation(EE问题，探索与开发)是计算广告和推荐系统里常见的一个问题，为什么会有EE问题？简单来说，是为了平衡推荐系统的准确性和多样性。

EE问题中的Exploitation就是：对用户比较确定的兴趣，当然要利用开采迎合，好比说已经挣到的钱，当然要花；而exploration就是：光对着用户已知的兴趣使用，用户很快会腻，所以要不断探索用户新的兴趣才行，这就好比虽然有一点钱可以花了，但是还得继续搬砖挣钱，不然花完了就得喝西北风。

2、Bandit算法

Bandit算法是解决EE问题的一种有效算法，我们先来了解一下Bandit算法的起源。Bandit算法来源于历史悠久的赌博学，它要解决的问题是这样的：

一个赌徒，要去摇老虎机，走进赌场一看，一排老虎机，外表一模一样，但是每个老虎机吐钱的概率可不一样，他不知道每个老虎机吐钱的概率分布是什么，那么每次该选择哪个老虎机可以做到最大化收益呢？这就是多臂赌博机问题（Multi-armed bandit problem, K-armed bandit problem, MAB）。

怎么解决这个问题呢？最好的办法是去试一试，不是盲目地试，而是有策略地快速试一试，这些策略就是Bandit算法。

Bandit算法如何同推荐系统中的EE问题联系起来呢？假设我们已经经过一些试验，得到了当前每个老虎机的吐钱的概率，如果想要获得最大的收益，我们会一直摇哪个吐钱概率最高的老虎机，这就是Exploitation。但是，当前获得的信息并不是老虎机吐钱的真实概率，可能还有更好的老虎机吐钱概率更高，因此还需要进一步探索，这就是Exploration问题。

下面，我们就来看一下一些经典的Bandit算法实现吧，不过我们还需要补充一些基础知识。

3、基础知识

3.1 累积遗憾

Bandit算法需要量化一个核心问题：错误的选择到底有多大的遗憾？能不能遗憾少一些？所以我们便有了衡量Bandit算法的一个指标：累积遗憾：

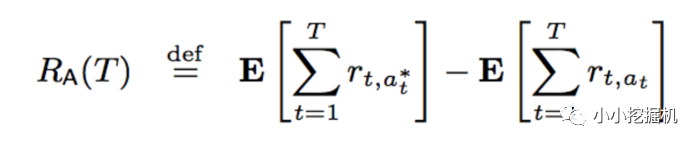
这里 t 表示轮数, r表示回报。公式右边的第一项表示第t轮的期望最大收益，而右边的第二项表示当前选择的arm获取的收益，把每次差距累加起来就是总的遗憾。

对应同样的问题，采用不同bandit算法来进行实验相同的次数，那么看哪个算法的总regret增长最慢，那么哪个算法的效果就是比较好的。

3.2 Beta分布

有关Beta分布，可以参考帖子：https://www.zhihu.com/question/30269898。这里只做一个简单的介绍。beta分布可以看作一个概率的概率分布。它是对二项分布中成功概率p的概率分布的描述。它的形式如下：

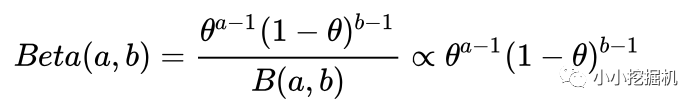
其中，a和b分别代表在a+b次伯努利试验中成功和失败的次数。我们用下面的图来说明一下Beta分布的含义：

上图中一共有三条线，我们忽略中间的一条线，第一条线中a=81，b=219。也就是说在我们进行了300次伯努利试验中，成功81次，失败219次的情况下，成功概率p的一个分布，可以看到，p的概率在0.27左右概率最大，但我们不能说成功的概率就是0.27，这也就是频率派和贝叶斯派的区别，哈哈。此时，我们又做了300次试验，此时在总共600次伯努利试验中，成功了181次，失败了419次，此时成功概率p的概率分布变味了蓝色的线，在0.3左右概率最大。

4、经典Bandit算法原理及实现

下文中的收益可以理解为老虎机吐钱的观测概率。

4.1 朴素Bandit算法

先随机试若干次，计算每个臂的平均收益，一直选均值最大那个臂。

4.2 Epsilon-Greedy算法

选一个(0,1)之间较小的数epsilon，每次以epsilon的概率在所有臂中随机选一个。以1-epsilon的概率选择截止当前，平均收益最大的那个臂。根据选择臂的回报值来对回报期望进行更新。

这里epsilon的值可以控制对exploit和explore的偏好程度，每次决策以概率ε去勘探Exploration，1-ε的概率来开发Exploitation，基于选择的item及回报，更新item的回报期望。

对于Epsilon-Greedy算法来首，能够应对变化，即如果item的回报发生变化，能及时改变策略，避免卡在次优状态。同时Epsilon的值可以控制对Exploit和Explore的偏好程度。越接近0，越保守，只想花钱不想挣钱。但是策略运行一段时间后，我们已经对各item有了一定程度了解，但没用利用这些信息，仍然不做任何区分地随机Exploration，这是Epsilon-Greedy算法的缺点。

4.3 Thompson sampling算法

Thompson sampling算法用到了Beta分布，该方法假设每个老虎机都有一个吐钱的概率p，同时该概率p的概率分布符合beta(wins, lose)分布，每个臂都维护一个beta分布的参数，即wins, lose。每次试验后，选中一个臂，摇一下，有收益则该臂的wins增加1，否则该臂的lose增加1。

每次选择臂的方式是：用每个臂现有的beta分布产生一个随机数b，选择所有臂产生的随机数中最大的那个臂去摇。

4.4 UCB算法

前面提到了，Epsilon-Greedy算法在探索的时候，所有的老虎机都有同样的概率被选中，这其实没有充分利用历史信息，比如每个老虎机之前探索的次数，每个老虎机之前的探索中吐钱的频率。

那我们怎么能够充分利用历史信息呢？首先，根据当前老虎机已经探索的次数，以及吐钱的次数，我们可以计算出当前每个老虎机吐钱的观测概率p'。同时，由于观测次数有限，因此观测概率和真实概率p之间总会有一定的差值 ∆ ，即p' - ∆ <= p <= p' + ∆。

基于上面的讨论，我们得到了另一种常用的Bandit算法：UCB(Upper Confidence Bound)算法。该算法在每次推荐时，总是乐观的认为每个老虎机能够得到的收益是p' + ∆。

好了，接下来的问题就是观测概率和真实概率之间的差值∆如何计算了，我们首先有两个直观的理解：1）对于选中的老虎机，多获得一次反馈会使∆变小，当反馈无穷多时，∆趋近于0，最终会小于其他没有被选中的老虎机的∆。2）对于没有被选中的老虎机，∆会随着轮数的增大而增加，最终会大于其他被选中的老虎机。

因此，当进行了一定的轮数的时候，每个老虎机都有机会得到探索的机会。UCB算法中p' + ∆的计算公式如下：

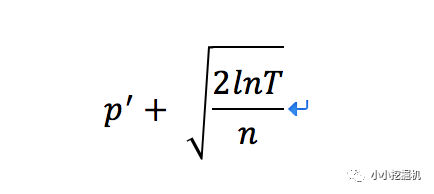
其中加号前面是第j个老虎机到目前的收益均值，后面的叫做bonus，本质上是均值的标准差，T是目前的试验次数，n是该老虎机被试次数。

为什么选择上面形式的∆呢，还得从Chernoff-Hoeffding Bound说起：

因此(下面的截图来自于知乎https://zhuanlan.zhihu.com/p/32356077)：

5、代码实现

接下来，我们来实现两个基本的Bandit算法，UCB和Thompson sampling算法。

5.1 UCB算法

代码中有详细的注释，所以我直接贴完整的代码了：

import numpy as np T = 1000 # T轮试验 N = 10 # N个老虎机 true_rewards = np.random.uniform(low=0, high=1, size=N) # 每个老虎机真实的吐钱概率 estimated_rewards = np.zeros(N) # 每个老虎机吐钱的观测概率，初始都为0 chosen_count = np.zeros(N) # 每个老虎机当前已经探索的次数，初始都为0 total_reward = 0 # 计算delta def calculate_delta(T, item): if chosen_count[item] == 0: return 1 else: return np.sqrt(2 * np.log(T) / chosen_count[item]) # 计算每个老虎机的p+delta，同时做出选择 def UCB(t, N): upper_bound_probs = [estimated_rewards[item] + calculate_delta(t, item) for item in range(N)] item = np.argmax(upper_bound_probs) reward = np.random.binomial(n=1, p=true_rewards[item]) return item, reward for t in range(1, T): # 依次进行T次试验 # 选择一个老虎机，并得到是否吐钱的结果 item, reward = UCB(t, N) total_reward += reward # 一共有多少客人接受了推荐 # 更新每个老虎机的吐钱概率 estimated_rewards[item] = ((t - 1) * estimated_rewards[item] + reward) / t chosen_count[item] += 1

5.2 Thompson sampling算法

Thompson sampling算法涉及到了beta分布，因此我们使用pymc库来产生服从beta分布的随机数，只需要一行代码就能在选择合适的老虎机。

np.argmax(pymc.rbeta(1 + successes, 1 + totals - successes))