递归与动态规划：基础例题分析

个人简介：一个热爱编程的在校生，我的世界不只有coding，还有writing。目前维护订阅号「苦逼的码农」，专注于写「算法与数据结构」，「Java」,「计算机网络」。

ps:最近几天正在刷一些有关动态规划的题，我会把自己学习时的想法以及做题的想法记录下来。

题目1：一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法

对于这道题，我第一眼看到的想法是用递归的做法的，用递归的方法做题，我觉得最重要的就是找出 这个函数与下一个函数之间的关系 以及 一个函数体结束的临界条件（即递归的结束）。

例如就本题而言,

1.第一步先找这个函数与下一个函数之间的关系：

假如有n个台阶，跳上一个n级的台阶的跳法总数为f(n).

我们在跳的过程中，每一次有两种跳法，即跳一个或两个台阶。

第一种跳法：第一次我跳了一个台阶，那么还剩下n-1个台阶还没跳，剩下的n-1个台阶的跳法有f(n-1)种。

或者用

第二种跳法：第一次跳了两个台阶，那么还剩下n-2个台阶还没，剩下的n-2个台阶的跳法有f(n-2)种。

由此不难得出递归公式：f(n) = (n-1) + f(n-2);

2.第二步，找出递归的结束条件

当n <= 0时，跳法为0，即此时f(n) = 0

当只剩下一个台阶n = 1时，那么只有一种跳法，即f(1) = 1;

当n = 2时，此时跳法为2种，即f(2) = 2;

函数与函数之间的关系以及递归的临界条件都找出来了，那么接下来就可以开始写代码了。如下所示：

不过观察一下你就会发现，其实在递归的过程中，有很多相同的)f(n)重复算。

如下图：

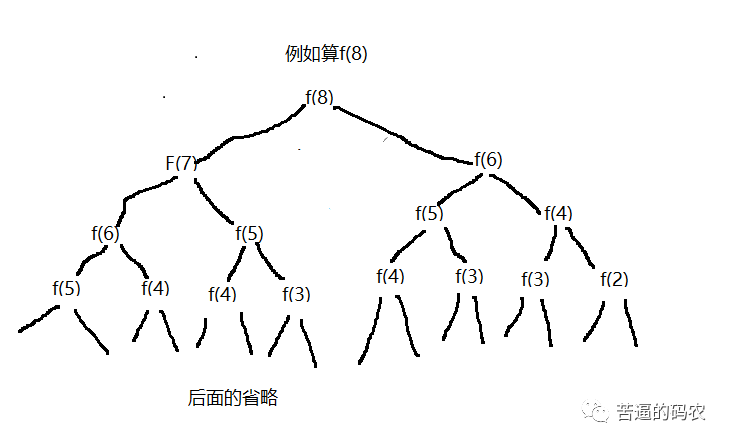
算一下你就知道，时间复杂度是指数级别的。如果是比赛这样做的话，绝对超时不通过

因此对于那些重复算过的，其实我们可以不用在重复递归来算它的，也就是所我们可以把f(n)算的结果一边给保存起来，这种就是动态规划的思想。

也就是说，我们可以把每次计算的结果保存中一个map容器里，把n作为key,f(n)作为value.然后每次要递归的时候，先查看一下这个f(n)我们是否已经算过了，如果已经算过了，我们直接从map容器里取出来返回去就可以了。如下：

这种方法会快很多很多。

实际上，对于f(n) = f(n-1) + f(n - 2)这种有递推关系的题，其实和斐波那契数列很相似，还可以这样做：

问题2： 一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。 求该青蛙跳上一个n级的台阶总共有多少种跳法。

分析，其实这道题和上面那道题一样的，只是本来每次跳有两种选择，现在有n中选择，即f(n) = f(n-1) + f(n - 2) + f(n-3)+.....+f(1);

因此做法如下：

如果你有其他想法，或者更完美的做法，欢迎指点江山。

下面为大家讲解另外两道，难度会提升一点点

数字三角形案例

题目描述 Description 下图给出了一个数字三角形，请编写一个程序，计算从顶至底的某处的一条路径，使该路径所经过的数字的总和最大。 注意：每一步可沿左斜线向下或右斜线向下

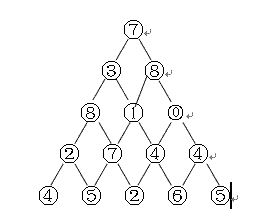
输入描述： 第1行是输入整数（如果该整数是0,就表示结束，不需要再处理），表示三角形行数n，然后是n行数样例输入： 5 7 3 8 8 1 0 2 7 4 4 4 5 2 6 5

解题思路：对于这种有多种选择的题，一般都可以使用递归的方法来做，上节讲过，对于递归的题，最重要的 就是找出递归的两个条件：

1. 两个函数之间存在的关系 2. 递归结束的临界条件

我们先来声明一些变量来记录一些东西

1. 用D(i,j)这个二维数组来记录这个数字三角形，i表示第i行，j表示第j列，D(i,j)表示第i行j列这个点的值 2. MaxSum(i, j) : 从D(r,j)到底边的各条路径中，最佳路径的数字之和(动态规划记录状态会用到) 3. state(i,j):用来记录D(i,j)这个点是否计算过，如果还没有计算过，则state(i,j) = -2,否则state(i,j) = MaxSum(i,j).

现在我们来寻找递归的两个条件

1. 我们从第0行开始一直走，显然，当我们走到最后一行时，递归结束，此时i = n-1(因为我们从第0行开始算)

2. 当我们处在D(i, j)这个点时，我们可以笔直往下走，也可以斜着往下走，有两种走法 。我们的目标时找出使总路径较大的点，可以得到递归公式：

MaxSum(i,j) = max{MaxSum(i+1, j), MaxSum(i+1, j+1)} + D(i, j)

找出了这两个条件，就好做了。代码如下：

int MaxSum(int i, int j){ if(i == n-1) return D[i][j];//最底层，把该点的路径值返回 int x = MaxSum(i + 1, j);//计算笔直向下走时的最优路径 int y = MaxSum(i + 1, j + 1);//计算斜向下走时的最优路径 return max(x,y) + D[i][j]; }

问题所在：

和上次讲的一样，这种递归属于暴力递归，会有很多重复计算的。和上次讲的跳台阶那个类似。时间复杂度是O(2的n次方)

重复计算的次数如下图所示

下面我们采用动态规划的方法（递归动态保存）

其实，我们可以每次在计算D(i,j)的时候，把计算出来的最优解MasSum(i,j)保存起来， 下次需要的时候，先查看D(i,j)是否之前计算过，如果计算过，直接取出来就可以了。前面说过我们把值存放在state(i,j)这个数组里。

代码如下所示

` int MaxSum(int i, int j){ if(i == num)//临界值 return D[i][j]; else if (state[i][j] != -2)//表示这个 点已经计算过了 { return state[i][j]//直接取出返回 }else//否则的话就只好乖乖计算 { int x = MaxSum(i + 1, j); int y = MaxSum(i + 1, j + 1); state[i][j] = max(x,y) + D[i][j];//保存起来 return state[i][j]; } }`

时间复杂度为O(n2)O(n2)，因为三角形的数字总和为n(n+1)/2n(n+1)/2

ps:其实这道题也可以用递推方法的动态递归来接，从底部往上算起，有兴趣的可以思考下。有兴趣且想不出的可以问我勒

二、

学这个最重要的就是多练些题了，刚开始的时候尽量找写简单点的题，函数与函数之间的递归关系比较容易 找的题。下面找给大家介绍道题，和上次讲的类型比较一样，算是比较基础的题：

问题： 我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？

还是我说的一样，找出

(1).递归的结束条件。

(2).函数与函数之间的递归关系

1.先找结束条件：

（1）当 n < 1时，显然不需要用2*1块覆盖，应该返回 0。

（2）当 n = 1时，只存在一种情况

（3）当 n = 2时，存在两种情况

（4）当 n > 2时，显然是需要横着放和竖着，这时两种情况交替放，就会产生递归的之间的函数关系（下图是n=3的情况）

即 f(n) = f(n-1) + f(n-2). (有木发现这些题都很类似，解法几乎一样)

代码如下所示

int f(int n){ if(n < 1)return 0    else if(n == 1)return 1    else if(n == 2)return 2    else return f(n-1) + f(n-2) }

老规矩，这样做，有很多重复算的，采用动态记录的方法。以n为key,f(n)为value保存在map容器中

Map m = new HashMap<>(); int f5(int n){ if(n < 1){            return 0;        }        else if(n == 1){            return 1;        }else if(n == 2){            return 2;        }else{            if(m.containsKey(n)){                return m.get(n);            }else{                int sum = f5(n-1) + f5(n-2);                map.put(n, sum);                return sum;            }        }    }