“深度学习”虽然深奥，本质却很简单

“深度学习”虽然深奥，本质却很简单。无论是图像识别还是语义分析，机器的“学习”能力都来源于同一个算法 — 梯度下降法 (Gradient Descent)。要理解这个算法，你所需要的仅仅是高中数学。在读完这篇文章后，你看待 AI 的眼光会被永远改变。

Google 研发了十年自动驾驶后，终于在本月上线了自动驾驶出租车服务。感谢“深度学习”技术，人工智能近年来在自动驾驶、疾病诊断、机器翻译等领域取得史无前例的突破，甚至还搞出了些让人惊艳的“艺术创作”：

Prisma 把你的照片变成艺术作品

AI 生成的奥巴马讲话视频，看得出谁是本尊吗？

开源软件 style2paints 能自动给漫画人物上色

如果不了解其中的原理，你可能会觉得这是黑魔法。

但就像爱情，“深度学习”虽然深奥，本质却很简单。无论是图像识别还是语义分析，机器的“学习”能力都来源于同一个算法 — 梯度下降法 (Gradient Descent)。要理解这个算法，你所需要的仅仅是高中数学。在读完这篇文章后，你看待 AI 的眼光会被永远改变。

一个例子

我们从一个具体的例子出发：如何训练机器学会预测书价。在现实中，书的价格由很多因素决定。但为了让问题简单点，我们只考虑书的页数这一个因素。

在机器学习领域，这样的问题被称为“监督学习 (Supervised Learning)”。意思是，如果我们想让机器学会一件事（比如预测书的价格），那就给它看很多例子，让它学会举一反三（预测一本从未见过的书多少钱）。其实跟人类的学习方法差不多，对吧？

现在假设我们收集了 100 本书的价格，作为给机器学习的例子。大致情况如下：

页数

书价

接下来我们要做两件事：

告诉机器该学习什么；

等机器学习。

告诉机器该学什么

为了让机器听懂问题，我们不能说普通话，得用数学语言向它描述问题，这就是所谓的“建模”。为了让接下来的分析更直观，我们把收集回来的例子画在数轴上：

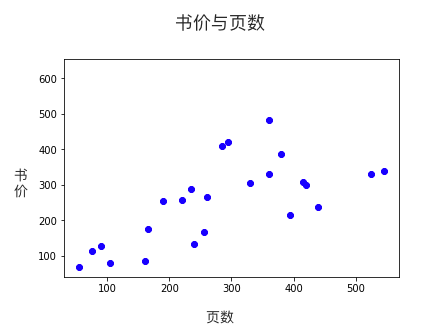
我们希望机器通过这些样本，学会举一反三，当看到一本从未见过的书时，也能预测价格。比如说，预测一本480页的书多少钱：

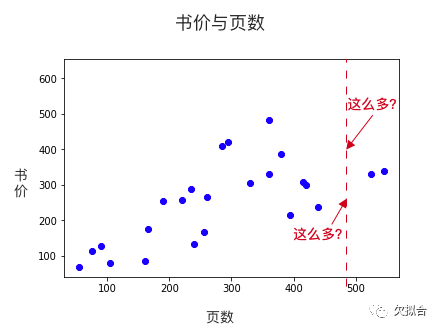
480页的书多少钱？

观察图表，我们能看出页数和书价大致上是线性关系，也就是说，我们可以画一根贯穿样本的直线，作为预测模型。

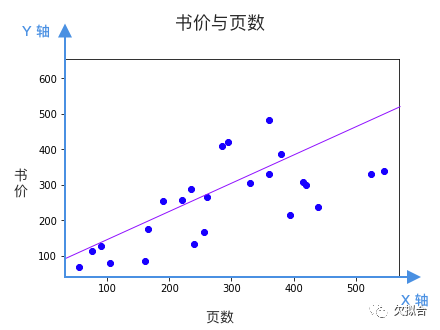
如果我们把页数看作 X 轴，书价看作 Y 轴，这根直线就可以表示为：

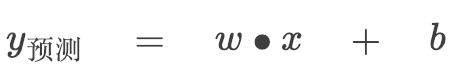
w 决定直线的倾斜程度，b 决定这根直线和 Y 轴相交的位置。问题是，看起来有很多条线都是不错的选择，该选哪条？换句话说 w 和 b 该等于多少呢？

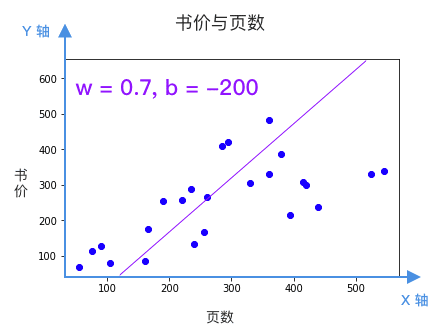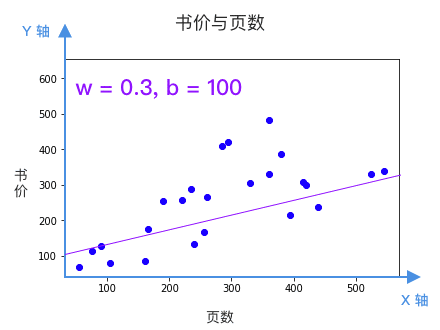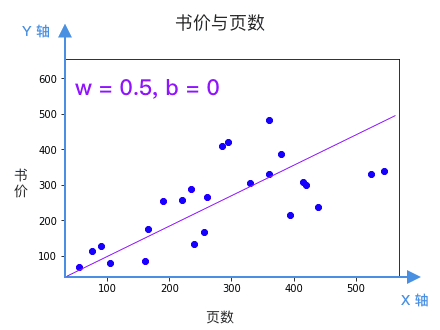
每根直线都是一个候选的模型，该选哪个？

显然，我们希望找到一根直线，它所预测的书价，跟已知样本的误差最小。换句话说，我们希望下图中的所有红线，平均来说越短越好。

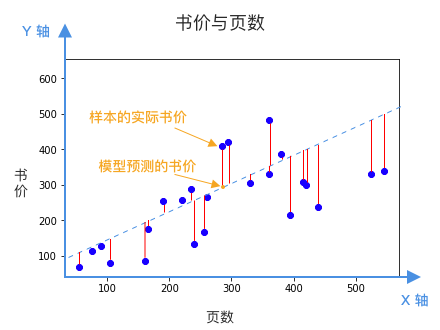
红线的长度，就是模型（蓝色虚线）预测的书价，和样本书价（蓝点）之间的误差。

红线的长度等于预测书价和样本书价的差。以第一个样本为例，55页的书，价格69元，所以第一根红线的长度等于：

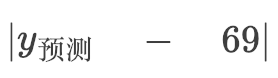
因为绝对值不便于后面的数学推导，我们加个平方，一样能衡量红线的长度。

因为我们的预测模型是：

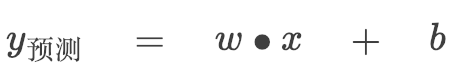
所以

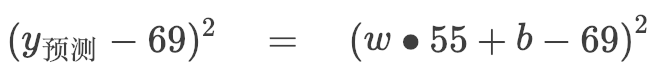
这个样本是一本 55 页，69 元的书。

算式开始变得越来越长了，但记住，这都是初中数学而已！前面提到，我们希望所有红线平均来说越短越好，假设我们有 100 个样本，用数学来表达就是：

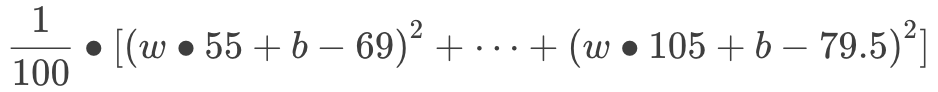
至此，我们把“预测书价”这个问题翻译成数学语言：“找出 w 和 b 的值，使得以上算式的值最小。”坚持住，第一步马上结束了！

我们现在有 2 个未知数：w 和 b。为了让问题简单一点，我们假设 b 的最佳答案是 0 好了，现在，我们只需要关注 w 这一个未知数：

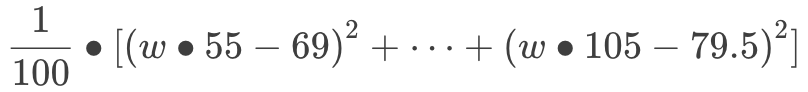
把括号打开：

在机器学习领域，这个方程被称为“代价 (cost) 函数”，用于衡量模型的预测值和实际情况的误差。我们把括号全打开：

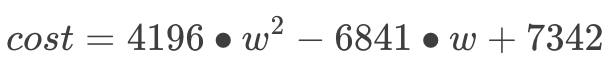
不用在意方程中的数字，都是我瞎掰的。

至此，我们把“预测书价”这个问题翻译成数学语言：“w 等于多少时，代价函数最小？”第一步完成！到目前为止，我们只用上了初中数学。

—

机器是怎么学习的

代价函数是个一元二次方程，画成图表的话，大概会是这样：

不用在意坐标轴上的具体数字，都是我瞎掰的。

前面讲到，机器要找到一个 w 值，把代价降到最低：

机器采取的策略很简单，先瞎猜一个答案（比如说 w 等于 20 ，下图红点），虽然对应的代价很高，但没关系，机器会用“梯度下降法”不断改进猜测。

如果你微积分学得很好，此时可能会问：求出导数函数为 0 的解不就完事了吗？在实际问题中，模型往往包含上百万个参数，它们之间也并非简单的线性关系。针对它们求解，在算力上是不现实的。

现在，我们得用上高中数学的求导函数了。针对这个瞎猜的点求导，导数值会告诉机器它猜得怎么样，小了还是大了。

如果你不记得导数是什么，那就理解为我们要找到一根直线，它和这条曲线只在这一个点上擦肩而过，此前以后，都无交集（就像你和大部分朋友的关系一样）。所谓的导数就是这根线的斜率。

我们可以看得出，在代价函数的最小值处（即曲线的底部）导数等于 0。如果机器猜测的点，导数大于 0，说明猜太大了，下次得猜小一点，反之亦然。根据导数给出的反馈，机器不断优化对 w 的猜测。因为机器一开始预测的点导数大于 0 ，所以接下来机器会猜测一个小一点的数：

机器接着对新猜测的点求导，导数不等于 0 ，说明还没到达曲线底部。

那就接着猜！机器孜孜不倦地循环着“求导 - 改进猜测 - 求导 - 改进猜测”的自我优化逻辑 —— 没错，这就是机器的“学习”方式。顺便说一句，看看下图你就明白它为什么叫做“梯度下降法”了。

终于，皇天不负有心机，机器猜到了最佳答案：

就这样，头脑简单一根筋的机器靠着“梯度下降”这一招鲜找到了最佳的 w 值，把代价函数降到最低值，找到了最接近现实的完美拟合点。

总结一下，我们刚刚谈论了三件事：

通过观察数据，我们发现页数与书价是线性关系——选定模型；

于是我们设计出代价函数，用来衡量模型的预测书价和已知样本之间的差距——告诉计算机该学习什么；

机器用“梯度下降法”，找到了把代价函数降到最低的参数 w ——机器的学习方法。

机器“深度学习”的基本原理就是这么简单。现在，我想请你思考一个问题：机器通过这种方法学到的“知识”是什么？

现实问题中的深度学习

为了让数学推演简单点，我用了一个极度简化的例子。现实中的问题可没那么简单，主要的差别在于：

现实问题中，数据的维度非常多。

今天在预测书价时，我们只考虑了页数这一个维度，在机器学习领域，这叫做一个“特征 (feature)”。

但假设我们要训练机器识别猫狗。一张 200 * 200 的图片就有 4 万个像素，每个像素又由 RGB 三个数值来决定颜色，所以一张图片就有 12 万个特征。换句话说，这个数据有 12 万个维度，这可比页数这一个维度复杂多了。好在，无论有多少个维度，数学逻辑是不变的。

现实问题中，数据之间不是线性关系。

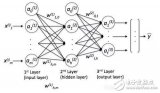
在今天的例子中，页数和书价之间是线性关系。但你可以想象得到，猫照片的 4 万个像素和“猫”这个概念之间，可不会是简单的线性关系。事实上两者之间的关系是如此复杂，只有用多层神经网络的上百万个参数（上百万个不同的 w：w1, w2, ..., w1000000）才足以表达。所谓“深度”学习指的就是这种多层网络的结构。

说到这里，我们可以回答前面的问题了：机器所学到的“知识”到底是什么？

就是这些 w。

在今天的例子中，机器找到了正确的 w 值，所以当我们输入一本书的页数时，它能预测书价。同样的，如果机器找到一百万个正确的 w 值，你给它看一张照片，它就能告诉你这是猫还是狗。

正因为现实问题如此复杂，为了提高机器学习的速度和效果，在实际的开发中，大家用的都是梯度下降的各种强化版本，但原理都是一样的。