浅析特征抽取的经典算法PCA

之前格物汇的文章给大家介绍过，随着近几年大数据技术的普及，企业可以获取海量数据，但是这些海量数据带给我们更多信息的同时，也带来了更多的噪音和异常数据，如何降维去噪成为很多企业关注的焦点。而特征抽取和特征选择都是降维的重要方法，针对于the curse of dimensionality(维数灾难)，都可以达到降维的目的，但是这两种方法有所不同。

>>>>

特征抽取（Feature Extraction)

Creatting a subset ofnew features by combinations of the exsiting features.也就是说，特征抽取后的新特征是原来特征的一个映射。

>>>>

特征选择（Feature Selection）

choosing a subset of allthe features(the ones more informative。也就是说，特征选择后的特征是原来特征的一个子集。

特征抽取是如何对数据进行变换的呢？其两个经典的方法：主成分分析(Principle Components Analysis ,PCA)和线性评判分析（LinearDiscriminant Analysis,LDA）给出了解答，今天我们就先来看一下什么是主成分分析。

什么是主成分分析

主成分分析（principal component analysis），PCA是其缩写。此方法是一种无监督线性转换技术，其目标是找到数据中最主要的元素和结构，去除噪音和冗余，将原有的复杂数据降维，揭露出隐藏在复杂数据背后的简单结构。

主成分分析就是试图在力保数据信息丢失最少的原则下，对这种多变量的数据表进行最佳综合简化。这些综合指标就称为主成分,也就是说，对高维变量空间进行降维处理，从线性代数角度来看，PCA目标是找到一组新正交基去重新描述得到的数据空间，这些新维度就是主成分。

PCA的原理

我们现在来看一下PCA算法是如何实现的，我们通过一个具体实例来理解，假设我们有这样一些标准化后的数据：[-1,-2],[-1,0],……,[2,1],[0,1]。我们写成向量的形式如下：

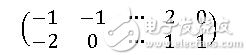
我们还可以在二维坐标系中画出来：

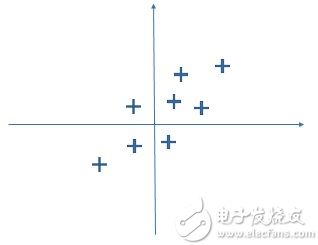
PCA主要的目的是降维简化数据，这些数据本就是二维，想要再降维则需要重新找一个方向，并把这些点映射到这个方向上（降到1维）。试想，怎么才能找到这个方向，且不损失大部分信息呢？PCA的做法是，找到新映射的方法需要满足如下两个原则：

在新映射的方向上每个数据的映射点方差尽可能大。因为方差大的数据所包含的信息量越大。

新映射的方向应彼此正交，这样映射出的坐标点选取才更有意义。

寻找新映射也可以看作基变换，我们可以不断旋转基，寻找满足上面两个原则的情况。如下图所示，中间的映射方向图里数据在新基上映射点的方差就比右边图映射点方差大的多。而方差大则表示该数据在该方向上含有的信息量多，反之另一个新基的方向上含有的信息量就少的多。如果这个方向上的信息量非常少，即使舍去也无伤大雅，我们就可以考虑将其舍去，实现降维的操作。

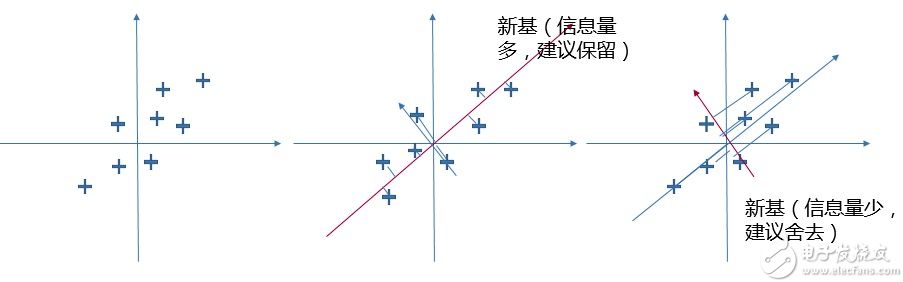
新基可以看成是由以前标准直角坐标系旋转而成，在线性代数中，这样的坐标轴旋转操作可以通过原本直角坐标系坐标乘转换矩阵得到：

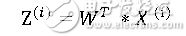
所以我们就将问题转换成找转移矩阵W上，如何去求W呢？我们希望降维后的数据要尽可能的与原数据非常接近（不丢失信息）。我们可以计算转换后的坐标Z与转换之前的坐标X之间的距离：

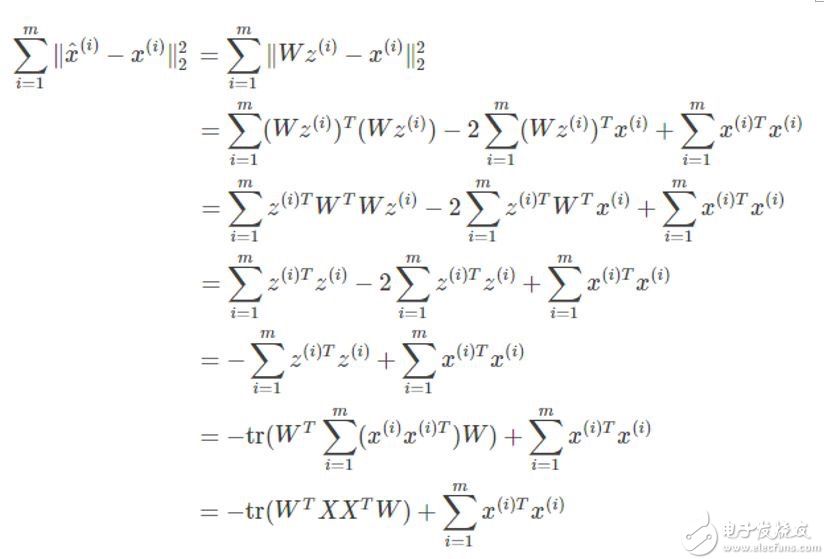
因此为了让转换距离最小，我们可以将问题等价转换成：

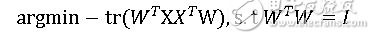
由于中间推导过程较为复杂，故在此省略，最后求解推导的结果为：

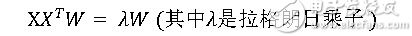
这不正是特征值的定义公式吗？所以只需要对协方差矩阵进行特征值分解，并将求得的特征值排序，取前N（PCA所要降低的目标维度）个特征值构成的向量W，即为PCA的解。

PCA优缺点

优点

（1）它是无监督学习，只与数据相关，无参数限制。

（2）通过PCA降维，可以达到简化模型和对数据进行压缩的效果。同时最大程度的保持了原有数据的信息。

（3）各主成分之间正交，可消除原始数据成分间的相互影响。

（4）计算方法简单，易于在计算机上实现。

缺点

（1）如果用户对观测对象有一定的先验知识，掌握了数据的一些特征，却无法通过参数化等方法对处理过程进行干预，可能会得不到预期的效果，效率也不高。

（2）贡献率小的主成分往往可能含有对样本差异的重要信息。

好了，今天格物汇的内容就到这里，近期我们还将介绍特征抽取的另一种方法LDA（线性评判分析），敬请期待。

本文作者：格创东智OT团队（转载请注明作者及来源）