TensorFlow回归：建立了一个模型来预测汽车的燃油效率。

今天的内容介绍的是回归问题。在回归问题中，我们的目标是预测连续值的输出，如价格或概率。将此与分类问题进行对比，我们的目标是预测离散标签（例如，图片里有一个苹果或一个橙子）。

本笔记采用了经典的 Auto MPG 数据集，并建立了一个模型来预测 20 世纪 70 年代末和 80 年代初汽车的燃油效率。为此，我们将为模型提供该时间段内许多模型的描述。此描述包括以下属性：气缸，排量，马力和重量。

此示例使用 tf.keras API，有关详细信息，请参阅指南

https://tensorflow.google.cn/guide/keras?hl=zh-CN

# Use seaborn for pairplot!pip install -q seaborn

from __future__ import absolute_import, division, print_functionimport pathlibimport pandas as pdimport seaborn as snsimport tensorflow as tffrom tensorflow import kerasfrom tensorflow.keras import layersprint(tf.__version__)

1.12.0

Auto MPG 数据集

该数据集可从UCI Machine Learning Repository 获得（https://archive.ics.uci.edu/）。

取得数据

首先下载数据集

dataset_path = keras.utils.get_file("auto-mpg.data", "https://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data")dataset_path

Downloading data from https://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data

32768/30286 [================================] - 0s 1us/step

'/root/.keras/datasets/auto-mpg.data'

使用 pandas 导入

column_names = ['MPG','Cylinders','Displacement','Horsepower','Weight', 'Acceleration', 'Model Year', 'Origin'] raw_dataset = pd.read_csv(dataset_path, names=column_names, na_values = "?", comment='\t', sep=" ", skipinitialspace=True)dataset = raw_dataset.copy()dataset.tail()

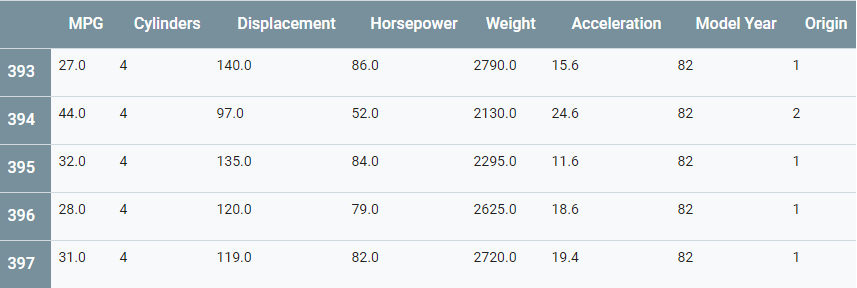
清理数据

数据集包含一些未知数值

dataset.isna().sum()

MPG 0Cylinders 0Displacement 0Horsepower 6Weight 0Acceleration 0Model Year 0Origin 0dtype: int64

删除那些行来保持本初始教程简单明了

dataset = dataset.dropna()

上方表格中，“Origin” 列实际上是分类，而不是数字。所以把它转换为one-hot：

origin = dataset.pop('Origin')

dataset['USA'] = (origin == 1)*1.0dataset['Europe'] = (origin == 2)*1.0dataset['Japan'] = (origin == 3)*1.0dataset.tail()

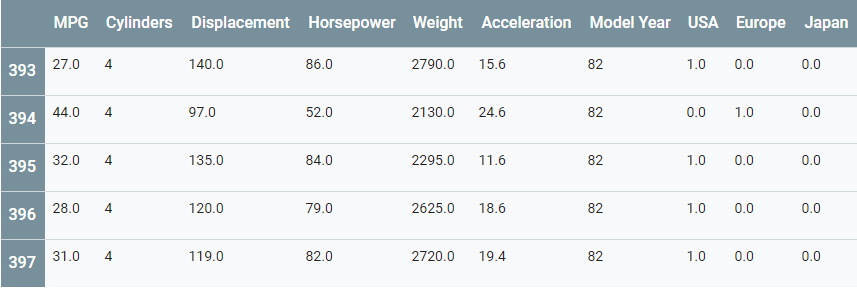
将数据拆分成训练和测试

现在将数据拆分成一个训练集和一个测试集。我们将在模型的最终评估中使用测试集。

train_dataset = dataset.sample(frac=0.8,random_state=0)test_dataset = dataset.drop(train_dataset.index)

检查数据

快速浏览训练集中几个对列的联合分布

sns.pairplot(train_dataset[["MPG", "Cylinders", "Displacement", "Weight"]], diag_kind="kde")

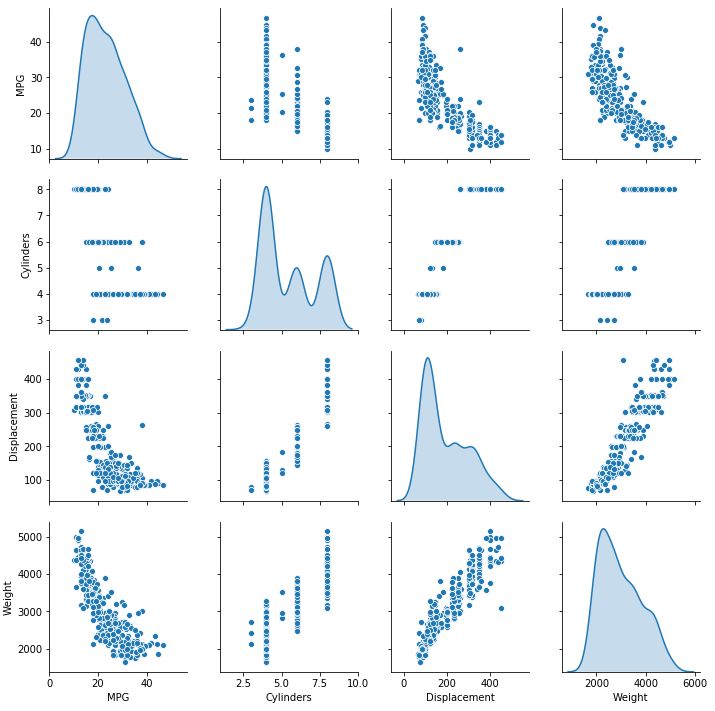
并查看这个整体统计数据：

train_stats = train_dataset.describe()train_stats.pop("MPG")train_stats = train_stats.transpose()train_stats

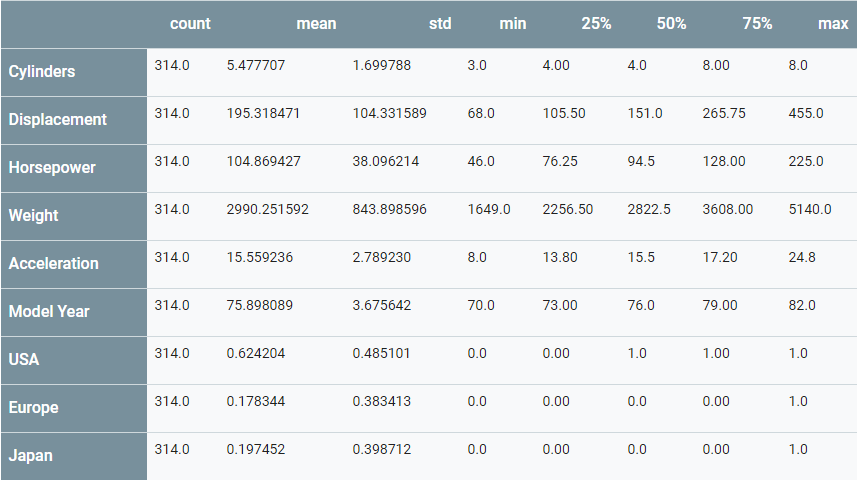
从标签中分割特征

将目标值或 “标签” 与特征分开。此标签是您将要训练模型进行预测的数值。

train_labels = train_dataset.pop('MPG')test_labels = test_dataset.pop('MPG')

将数据规范化

再次查看上面的train_stats 块，并注意一下，每个特征的范围有多么的大相径庭。

使用不同比例和范围进行特征规范化是一个不错的做法。尽管模型可能在没有特征归一化的情况下收敛，但它会使训练更加困难，并且它使得结果模型依赖于输入中使用的单位的选择。

注意：我们故意只使用来自训练集的统计数据，这些统计数据也将被用于评估。这样模型就没有关于测试集的任何信息。

defnorm(x): return(x - train_stats['mean']) / train_stats['std']normed_train_data = norm(train_dataset)normed_test_data = norm(test_dataset)

这个规范化的数据是我们用来训练模型的数据。

注意：此处用于规范化输入的统计信息与模型权重同样重要。

模型

建模

让我们建立我们的模型。在这里，我们将使用具有两个密集连接的隐藏层的 Sequential 模型，以及返回单个连续值的输出层。模型构建步骤包含在一个函数 build_model 中，因为我们稍后将创建第二个模型。

def build_model(): model = keras.Sequential([ layers.Dense(64, activation=tf.nn.relu, input_shape=[len(train_dataset.keys())]), layers.Dense(64, activation=tf.nn.relu), layers.Dense(1) ]) optimizer = tf.train.RMSPropOptimizer(0.001) model.compile(loss='mse', optimizer=optimizer, metrics=['mae', 'mse']) return model

model = build_model()

检查模型

使用 .summary 方法打印模型的简单描述

model.summary()

_________________________________________________________________Layer (type) Output Shape Param # =================================================================dense (Dense) (None, 64) 640 _________________________________________________________________dense_1 (Dense) (None, 64) 4160 _________________________________________________________________dense_2 (Dense) (None, 1) 65 =================================================================Total params: 4,865Trainable params: 4,865Non-trainable params: 0_________________________________________________________________

现在来试一试这个模型。从训练数据中取出一批 10 个示例并调用 model.predict。

example_batch = normed_train_data[:10]example_result = model.predict(example_batch)example_result

array([[ 0.08682194], [ 0.0385334 ], [ 0.11662665], [-0.22370592], [ 0.12390759], [ 0.1889237 ], [ 0.1349103 ], [ 0.41427213], [ 0.19710071], [ 0.01540279]], dtype=float32)

它看上去起效了，产生预期的形状和类型的结果。

训练模型

该模型经过 1000 个 epoch 的训练，并在历史对象中记录训练和验证的准确性。

# Display training progress by printing a single dot for each completed epochclass PrintDot(keras.callbacks.Callback): def on_epoch_end(self, epoch, logs): if epoch % 100 == 0: print('') print('.', end='')EPOCHS = 1000history = model.fit( normed_train_data, train_labels, epochs=EPOCHS, validation_split = 0.2, verbose=0, callbacks=[PrintDot()])

................................................................................................................................................................................................................................................................................................................................................................................................................

使用存储在历史对象中的统计数据将模型的训练进度可视化。

hist = pd.DataFrame(history.history)hist['epoch'] = history.epochhist.tail()

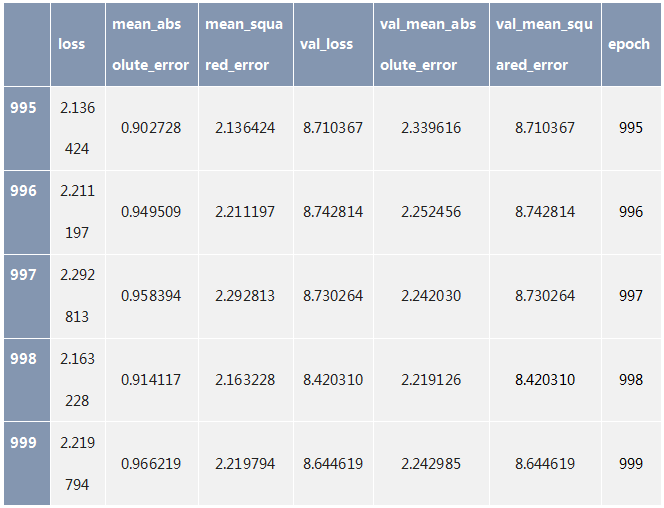
import matplotlib.pyplot as pltdef plot_history(history): plt.figure() plt.xlabel('Epoch') plt.ylabel('Mean Abs Error [MPG]') plt.plot(hist['epoch'], hist['mean_absolute_error'], label='Train Error') plt.plot(hist['epoch'], hist['val_mean_absolute_error'], label = 'Val Error') plt.legend() plt.ylim([0,5]) plt.figure() plt.xlabel('Epoch') plt.ylabel('Mean Square Error [$MPG^2$]') plt.plot(hist['epoch'], hist['mean_squared_error'], label='Train Error') plt.plot(hist['epoch'], hist['val_mean_squared_error'], label = 'Val Error') plt.legend() plt.ylim([0,20])plot_history(history)

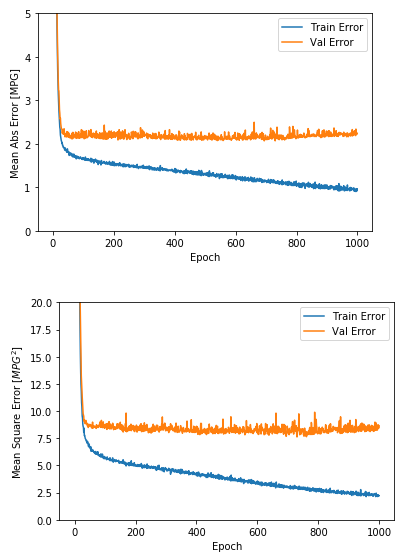
该图显示数百个 epoch 后的验证错误几乎没有改善，甚至降低了。让我们更新 model.fit 方法，以便在验证分数没有提高时自动停止训练。我们将使用一个回调测试每个 epoch 的训练条件。如果经过一定数量的时期而没有显示出改进，则自动停止训练。

您可以在

https://tensorflow.google.cn/api_docs/python/tf/keras/callbacks/EarlyStopping?hl=zh-CN了解有关此回调的更多信息。

model = build_model()# The patience parameter is the amount of epochs to check for improvementearly_stop = keras.callbacks.EarlyStopping(monitor='val_loss', patience=50)history = model.fit(normed_train_data, train_labels, epochs=EPOCHS, validation_split = 0.2, verbose=0, callbacks=[early_stop, PrintDot()])plot_history(history)

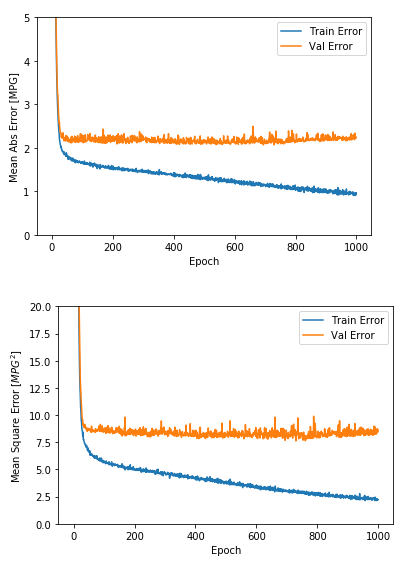
该图表显示在验证集上，平均误差通常在 +/- 2 MPG 左右。这个结果好吗？ 我们将决定权留给你。

让我们看看模型在测试集上是如何执行的，在训练模型时我们并没有使用它：

loss, mae, mse = model.evaluate(normed_test_data, test_labels, verbose=0)print("Testing set Mean Abs Error: {:5.2f} MPG".format(mae))

Testing set Mean Abs Error: 1.88 MPG

作出预测

最后，使用测试集中的数据预测 MPG 值：

test_predictions = model.predict(normed_test_data).flatten()plt.scatter(test_labels, test_predictions)plt.xlabel('True Values [MPG]')plt.ylabel('Predictions [MPG]')plt.axis('equal')plt.axis('square')plt.xlim([0,plt.xlim()[1]])plt.ylim([0,plt.ylim()[1]])_ = plt.plot([-100, 100], [-100, 100])

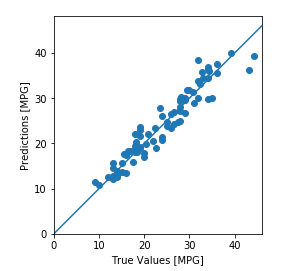
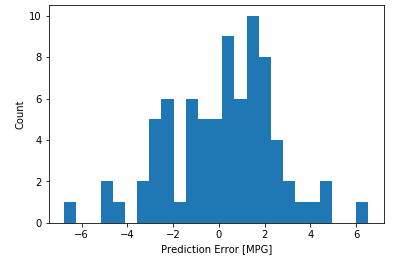
error = test_predictions - test_labelsplt.hist(error, bins = 25)plt.xlabel("Prediction Error [MPG]")_ = plt.ylabel("Count")

结论

本笔记介绍了一些处理回归问题的技巧：

均方误差（MSE）是用于回归问题的常见损失函数（与分类问题不同）

同样，用于回归的评估指标与分类不同。常见的回归指标是平均绝对误差（MAE）

当输入数据要素具有不同范围的值时，应单独缩放每个要素

如果训练数据不多，则选择隐藏层较少的小型网络，以避免过度拟合

防止过度装配的一个有用的技术是尽早停止