机器学习所需的数学知识你能够有效使用吗

开始机器学习之旅，需要什么层次的数学功底？ 尤其是对于那些没有学过数学和统计学的同学们来说，这个问题当前不甚清楚，在这篇文章中，我将要为那些使用机器学习技术来开发产品或做学术研究的人们提供一些数学背景方面的建议。这些建议源于我与机器学习工程师、研究人员和教育工作者的对话，以及我在机器学习研究和产业方面的独到经验。

为了构造（机器学习中）数学的背景，我会先讲一些与传统课堂不同的思维模式和策略。然后，我会概述不同类型机器学习工作所需的具体背景，毕竟机器学习涉及的学科范围太广泛了（它涵盖了高中级别的统计和微积分，也涵盖了概率图形模型（PGM）的最新进展）。

我希望读者们在读到文章的最后时，能够知道自己有效使用机器学习所必需的数学知识。

作为这篇文章的前言，我想说：对于不同学习者的个人需求或目标来说，学习的风格、架构和资源都应该是独一无二的！

数学焦虑症的小贴士

事实证明，很多人——包括工程师——都害怕数学。首先，我想谈谈“擅长数学”这类传说。

事实是，擅长数学的人都做过大量的数学练习。因此，在研究数学问题被卡住时，他们依然能够“风雨不动安如山”。如最近的研究所示，学生的心态，而非先天才能，才是预测一个人学习数学的能力的主要因素。

要清楚的是，要达到这种境界，需要时间和精力。这显然不是你天生就有的能力。本文的剩余部分将帮助您确定所需的数学功底，并概述构建它的策略。

万事开头难 作为软性先修数学条件，我们假设你对线性代数/矩阵微积分都有了解，这样你就不会为奇怪的符号苦恼。同时我们还假设你有基础的概率知识。我们鼓励你拥有基本的编程能力，这是领悟机器学习中的数学的有力工具。之后，你可以根据你感兴趣的内容调整你的学习重点。

如何在课外学习数学？

我相信学习数学的最佳方式是以学生的身份全职学习。脱离了学校的环境，你可能不太容易获得系统的知识结构、正能量的同学压力和其他可用资源。

为了在课外学习数学，我建议大家将学习小组或午餐研讨会作为学习的重要途径。在研究型的实验室中，这可能以阅读小组的形式呈现。在构建知识结构方面，你的小组可以把教科书各章节过一遍，并定期对课程进行讨论，同时通过Slack平台的途径参与远程问答。

这里，企业文化发挥着重要的作用——这种“额外”的研究学习应该受到管理层的鼓励和激励，而不是被视为影响产品交付的消极怠工行为。事实上，虽然短期内会花费一些成本，但是构建同伴驱动的学习环境可以使你在长期的工作中更有效率。

数学与代码 在机器学习工作流程中，数学和代码紧密结合。代码通常直接由数学直觉构建，有时它甚至会和数学符号使用相同的句法。事实上，现代数据科学框架应用（例如NumPy）使得数学运算（例如矩阵/矢量积）与可读代码之间的转换变得直观和有效。

我鼓励你将编写代码作为巩固学习的一种方式。学习数学和编写代码都依赖于你对问题理解和表述的精准程度。例如，手动编写损失函数或优化算法，就是真正理解这些基础概念的好方法。

让我们来探索一个实际的问题：在你的神经网络中实现ReLU函数激活的反向传播（是的，即使Tensorflow / PyTorch可以替你做这个！）。这里简单介绍一下，反向传播是一种依赖于微积分链式规则来有效计算梯度的技术。为了在这个问题设定下使用链式规则，我们将上游导数与ReLU函数的梯度相乘。

我们先将ReLU激活函数进行可视化（就是下图的样子），然后这样定义这个函数：

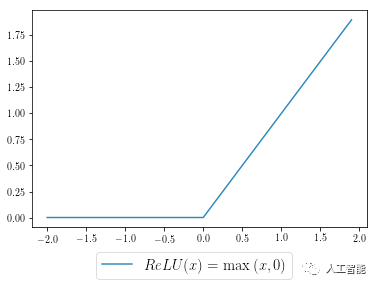
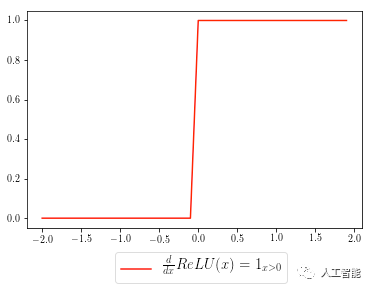
为了计算函数的梯度（直观来说就是斜率），你可以想象出这样一下分段函数，如下面的指示函数所示：

NumPy为我们提供了有用且直观的语法——我们的激活函数（蓝色曲线）可以通过代码表述出来，其中x是我们的输入，relu是我们的输出：

relu = np.maximum(x, 0)

ReLU函数的梯度函数（红色曲线）可以如下所示，grad表示上游梯度：

grad[x < 0] = 0

在没有首先自己推导梯度公式的情况下，这行代码可能没有任何意义。在我们的代码中，对于满足[h <0]条件（即x<0）的所有元素，将其对应上游激活函数的梯度（grad）数值设置为0。在数学上，这实际上相当于ReLU梯度函数的分段表示，所有x轴上小于0的数值，当乘以上游梯度时，它的值会变成0。

正如我们所见，通过我们对微积分的基本理解，我们可以清楚地理解代码的含义。

构建机器学习产品必需的数学知识

为了介绍这一节，我与机器学习工程师进行了交谈，确定了数学在调试系统时最有力的地方。以下是工程师基于数学见解回答的问题示例。

如果你还没有遇到过它们，请不要担心。希望本节能够为你提供一些特定问题的相关内容，也许你也会遇到类似的问题并尝试解决哟！

Q：我该用哪种聚类方法可视化高维的客户数据呢？

A：PCA或者tSNE。

Q：我该如何校准用来阻隔虚假用户交易的安全阈值（例如在0.9或0.8的置信水平下）？

A：可以使用概率校准（Probability calibration）。

Q：描述我卫星数据在世界特定地区（如硅谷与阿拉斯加州）的偏差的最佳方法是什么？

A：这是一个开放的研究型问题。也许可以基于“人口平价”（demographic parity，该方法是要求预测必须与某特定敏感属性不相关）的原则展开。

通常，统计和线性代数可以通过某种方式应用于这些问题中的任何一个。但是，要获得满意的答案通常需要针对特定领域的方法。如果是这样的话，你如何缩小你所需学习的数学范畴呢？

定义一个系统我们并不缺乏资源（例如数据分析使用scikit-learn，深度学习使用keras）去帮助我们进行系统建模。而在建模之前，我们需要围绕将要被建模的系统考虑这些问题：

系统的输入/输出分别是什么？

应该如何准备好合适的数据格式，从而适应系统要求？

如何进行特征建模或数据整理，以便于模型的推广？

如何为需要解决的问题设定合理的目标？

你会惊讶地发现——要定义一个系统，其实非常复杂。而搭建数据工作流（data pipeline）也并不容易。换句话说，构建一个机器学习产品需要进行大量的繁琐复杂的工作；而这些工作并不需要太深的数学背景。

数学需要“按需学习”当你一头扎进一个机器学习的任务中时，会发现其中有些步骤对你来说难以进行，这种情况在进行算法调试时尤为常见。当你停滞其中时，是否知道该如何解决这一窘境呢？你设定的权重是否合理？

为什么模型没有按照某个损失定义进行收敛？衡量成功的正确指标是什么？此时，有一些方法可以帮助到你：对数据做出假设、以不同方式约束优化、或尝试不同的算法。

通常，你会发现建模/调试过程中需要数学直觉（例如，选择损失函数或评估指标），这些直觉可能有助于做出明智的工程决策。 这些是你学习的机会！

来自Fast.ai的Rachel Thomas是这种“按需”方法的支持者——在教育学生时，她发现对于深度学习的学生来说，让他们对将要学习的内容感到兴奋更为重要。之后，针对这些学生的数学教育即可“按需”填补之前未涉及的知识漏洞。

接下来我将介绍对研究性工作中的机器学习方法有用的数学思维方式。批判性的观点认为，机器学习研究方法就像是就像是“拿来主义”，人们只是通过把更多运算扔进模型中，从而获得更好的预测表现。在一些圈子里，研究人员对实证研究方法仍然持怀疑态度，认为这些方法缺乏数学上的严谨性（例如某些深度学习方法），这些方法是不能将人类智慧发挥到极致的。

值得关注的是，研究界是建立在现有系统和假设的基础上，而这些系统和假设可能不会扩展我们对该领域的基本理解。研究人员需要提供新的基本模块，供我们在该领域中获取全新洞察力和方法。

这可能意味着我们需要像“深度学习教父” Geoff Hinton在他最近的Capsule Networks论文中所做的那样 ，重新思考构建某些领域的基础知识（如应用于图形分类的卷积神经网络）。

为了迈出下一步，我们需要提一些基本问题。这需要在数学方面的极度熟练——深度学习一书的作者Michael Nielsen称之为“有趣的探索”。这个过程涉及数千小时停滞、提问、重新思考问题以探索新观点。

“有趣的探索”使科学家们能够提出深刻，富有洞察力的问题，而不仅仅是简单的想法或架构的结合。显而易见，想要学会机器学习研究领域内需要的所有知识，是不可能的任务！要正确地进行“有趣的探索”，你需要遵循自己的兴趣，而不是为最热门的新结果感到焦虑。

机器学习研究是一个非常丰富的研究领域。当然，它在公平性、可解释性和可获得性方面也存在亟待解决的问题。在所有科学学科中都是如此，基本思维的获得并不能一蹴而就。要在解决关键问题所需的高水平数学框架的广度进行思考，需要长期的耐心。

将机器学习研究“大众化”希望我没有把“研究数学”描绘得太深奥，因为这些通过数学而产生的思考应该以直观的形式呈现！可悲的是，许多机器学习论文仍然充斥着复杂且不一致的术语，使关键的直觉难以被辨别。作为一名学生，你可以尝试将密集的论文翻译成容易被直观理解和消化的小块文章，通过博客和推特等发表，这将对你自己和这个领域大有裨益。你甚至可以从distill.pub中找些例子，当作解释机器模型研究方法结果的读物。换句话说，将技术思想的祛魅化作“有趣的探索”手段——你自己的学习（和机器学习Twitter）会感谢你的！主要领悟总的来说，我希望这篇文章为你提供了一个思考研究机器学习所需数学教育的开端。

不同的问题需要不同程度的直觉，我鼓励你首先弄清楚你的目标是什么。

如果你希望构建产品，请通过问题寻找同行和学习小组，并深入研究最终目标，激发你的学习。

在研究领域，广泛的数学基础可以为你提供工具，通过提供新的基础知识来推动该领域的发展。