导向滤波(Guided Filter)的解析与实现

现在从一个最简单的情形来开始我们的讨论。假设有一个原始图像 pp，其中含有一些噪声，欲将这些噪声滤出，最简单的、最基本的方法，大家可能会想到采用一些低通滤波器，例如简单平滑（也称Box Filter）或者高斯平滑等。滤波之后的图像为qq，如下图所示，图像qq中第ii个像素是由图像pp中以第ii个像素为中心的一个窗口ww中的像素确定的。

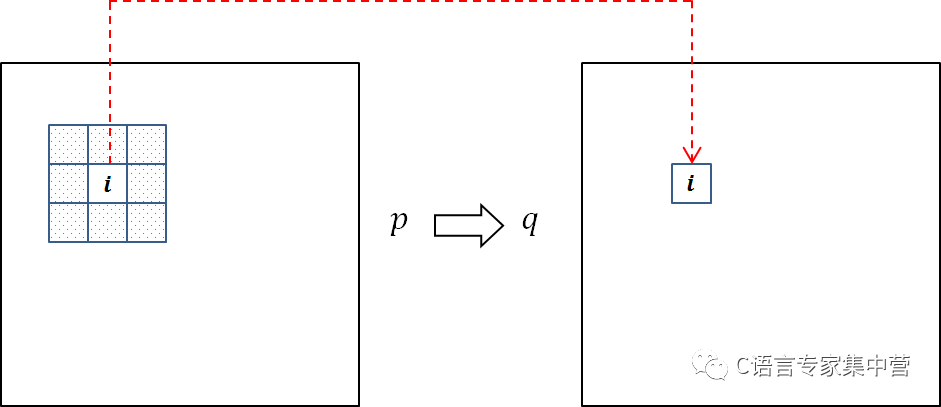
具体而言，在简单平滑中，图像qq中第ii个像素是由图像pp中以第ii个像素为中心的一个窗口ww中的所有像素取平均而得来的，即

qi=∑j∈wiWij⋅pj

其中，Wij=1/nWij=1/n，nn是窗口ww中的像素数目。也就是说，在简单平滑中，以像素ii为中心的一个窗口ww中的像素具有等同的权值。但是在高斯平滑中，权值WijWij将服从二维的高斯分布，结果导致离像素ii更接近的像素将具有更高的权重，反之离像素ii较远的像素则具有更小的权重。

无论是简单平滑，还是高斯平滑，它们都有一个共同的弱点，即它们都属于各向同性滤波。我们都知道，一幅自然的图像可以被看成是有（过渡平缓的，也就是梯度较小）区域和（过渡尖锐的，也就是梯度较大）边缘（也包括图像的纹理、细节等）共同组成的。噪声是影响图像质量的不利因素，我们希望将其滤除。噪声的特点通常是以其为中心的各个方向上梯度都较大而且相差不多。边缘则不同，边缘相比于区域也会出现梯度的越变，但是边缘只有在其法向方向上才会出现较大的梯度，而在切向方向上梯度较小。

因此，对于各向同性滤波（例如简单平滑或高斯平滑）而言，它们对待噪声和边缘信息都采取一直的态度。结果，噪声被磨平的同时，图像中具有重要地位的边缘、纹理和细节也同时被抹平了。这是我们所不希望看到的。研究人员已经提出了很多Edge-perserving的图像降噪（平滑）算法，例如双边滤波、自适应（维纳）平滑滤波（请参见文献【1】）、基于PM方程的各向异性滤波以及基于TV-norm的降噪算法等。本文将考虑在文献【2】中提出的另外一种Edge-perserving的图像滤波（平滑）算法——导向滤波（Guided Filter）。当然，通过阅读文献【2】，我们也知道导向滤波的应用不止有Edge-perserving的图像平滑，还包括图像去雾、图像Matting等等。

欢迎关注白马负金羁的博客 http://blog.csdn.net/baimafujinji，为保证公式、图表得以正确显示，强烈建议你从该地址上查看原版博文。本博客主要关注方向包括：数字图像处理、算法设计与分析、数据结构、机器学习、数据挖掘、统计分析方法、自然语言处理。

算法原理

导向滤波之所以叫这个名字，因为在算法框架中，要对pp进行滤波而得到qq，还得需要一个引导图像II。此时，滤波器的数学公式为

qi=∑j∈wiWij(I)⋅pj

注意，这里的Wij(I)Wij(I)就表示由引导图像II来确定加权平均运算中所采用的权值。注意，引导图像可以是单独的一幅图像，也可以输入的图像pp本身。当引导图像就是pp本身的时候，导向滤波就变成了一个Edge-perserving的滤波器，因此可以用于图像的平滑降噪。

导向滤波滤波的示意图如下所示（图片来自作者原文【2】）。注意这也是导向滤波所依赖的一个重要假设——导向滤波器在导向图像II和滤波输出qq之间在一个二维窗口内是一个局部线性模型，aa和bb是当窗口中心位于kk时该线性函数的系数，即qi=akIi+bi,∀i∈wkqi=akIi+bi,∀i∈wk。导引图像与qq之间存在线性关系，这样设定是因为我们希望导引图像提供的是信息主要用于指示哪些是边缘哪些是区域，所以在滤波时，如果导引图告诉我们这里是区域，那么就将其磨平。如果导引图告诉我们这里是边缘，这在最终的滤波结果里就要设法保留这些边缘信息。只有当II和qq之间是线性关系的这种引导关系才有意义。

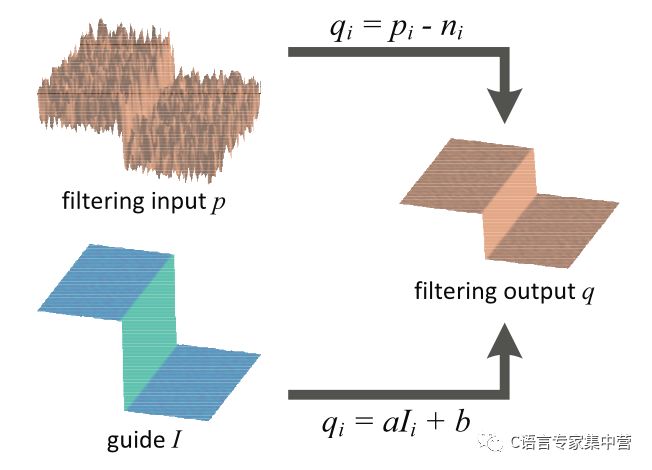
你可以想象一种情况来理解这种假设。II中的甲处和乙处都是区域，而丙处是边缘。那甲处的梯度和乙处的梯度应该不会相差太大，例如乙处的梯度是甲处梯度的1.5倍。但是由于丙处是边缘，所以丙处的梯度会比较大，例如可能是甲处的6倍，也就是乙处的4倍。如果II和qq之间满足线性关系，那么甲乙丙的梯度大小和倍数关系就都不会被扭曲。否则，如果二者之间的关系是非线性的，那么可能的结果是在qq中，尽管丙处的梯度仍然大于乙处的梯度，进而大于甲处的梯度，但是倍数关系可能会扭曲。例如，丙处的梯度是乙处的1.5倍，而是甲处的6倍（即乙处的梯度是甲处的4倍），这时你就会想象，甲处是区域，而乙处和丙处就变成了边缘。可见非线性关系会使得引导图像对于边缘和区域的指示作用发生错乱。

现在已知的是II和pp，要求的是qq。而如果能求得参数aa和bb，显然就能通过II和qq之间的线性关系来求出II。另一方面，还可以知道pp是qq受到噪声污染而产生的退化图像，假设噪声是nn，则有qi=pi−niqi=pi−ni。根据无约束图像复原的方法（可以参考【4】），这时可以设定最优化目标为min||n||min||n||，等价地有minn2minn2，即min∑i∈wk(qi−pi)2min∑i∈wk(qi−pi)2，于是有

argmin∑i∈wk(akIi+bk−pi)2

argmin∑i∈wk(akIi+bk−pi)2

于是便得到了一个最小二乘问题。但是我们也知道普通最小二乘有时候引起一些麻烦，因此要适当地引入惩罚项，即采用正则化的手段。原作者在处理这里时所采用的方法借鉴了从普通线性回归改进到岭回归时所采用的方法（如果你对正则化、岭回归、或者最小二乘法还不够清楚，那么你可以参考文献【5】），即求解下面这个最优化（最小化）目标所对应的参数aa和bb。

E(ak,bk)=∑i∈wk[(akIi+bk−pi)2+ϵa2k]

求解上述最优化问题（跟最小二乘法的推导过程一致），便会得到：

ak=1|w|∑i∈wkIipi−μipk¯σ2k+ϵbk=pk¯−akμk

其中，μkμk是II中窗口wkwk中的平均值，σ2kσk2是II中窗口wkwk中的方差，|w||w|是窗口wkwk中像素的数量，pk¯pk¯是待滤波图像pp在窗口wkwk中的均值，即pk¯=1|w|∑i∈wkpipk¯=1|w|∑i∈wkpi。

此外，在计算每个窗口的线性系数时，我们可以发现一个像素会被多个窗口包含，也就是说，每个像素都由多个线性函数所描述。因此，如之前所说，要具体求某一点的输出值时，只需将所有包含该点的线性函数值平均即可，如下

qi=1|w|∑k:i∈wk(akIi+bk)=ai¯Ii+bi¯

qi=1|w|∑k:i∈wk(akIi+bk)=ai¯Ii+bi¯

其中，ai¯=1|w|∑k∈wiakai¯=1|w|∑k∈wiak，bi¯=1|w|∑k∈wibkbi¯=1|w|∑k∈wibk。

下面给出导向滤波算法的流程，fmeanfmean为一个窗口半径为rr的均值滤波器（对应的窗口大小为2r+12r+1），corr为相关，var为方差，cov为协方差。

基于MATLAB的算法实现

下面来在MATLAB中具体实现一下导向滤波算法（代码来自Dr. Kaiming He，使用时请尊重原作者权利）。

上述代码的实现完全遵照上一小节最后给出的算法流程图。这里需要略作解释的地方是函数boxfilter，它是基于积分图算法实现的Box Filter。关于Box Filter，你也可以参考文献【6】以了解更多。首先来看看它到底做了些什么（因为这个Box Filter 和通常意义上的均值滤波并不完全一样）。

A =

1 1 1

1 1 1

1 1 1

>> B = boxfilter(A, 1);

>> B

B =

4 6 4

6 9 6

4 6 4

从上述代码可以看到，当参数r=1时，此时的滤波器窗口是3×33×3。将这样大小的一个窗口扣在原矩阵中心，刚好可以覆盖所有矩阵，此时求和为9，即把窗口里覆盖到的值全部加和。此外当把窗口中心挪动到左上角的像素时，因为窗口覆盖区域里只有4个数字，所以结果为4。所以你可以看出这里的Box Filter只是做了求和处理，并没有归一化，所以并不是真正的均值滤波（简单平滑）。必须结合后面的一句

mean_I = boxfilter(I, r) ./ N;

1

才算是完成了均值滤波。而这整个过程就相当于文献【6】中介绍的函数imboxfilt。但是你会发现它们二者在执行的时候最终的结果（主要是位于图像四周边缘的数值）会有细微的差异。这是因为MATLAB中的imboxfilt函数在处理位于图像四周边缘的像素时，需要虚拟地为原图像补齐滤波窗口覆盖但是没有值的区域。

下面给出上述boxfilter函数的实现代码。

上述代码基于积分图实现，如果你对积分图不是很了解，可以参考其他文献，这里不再赘述。

下面我们来实验一下上述导引滤波用于edge-perserving的平滑滤波效果。

I = double(imread('cat.bmp')) / 255;

p = I;

r = 4; % try r=2, 4, or 8

eps = 0.2^2; % try eps=0.1^2, 0.2^2, 0.4^2

O = guidedfilter(I, p, r, eps);

subplot(121), imshow(I);

subplot(122), imshow(O);

执行上述代码，结果如下所示。可见效果还是很不错的。但是我们可以来做一下事后分析，看看导向滤波是如果实现edge-perserving的平滑滤波效果的。当I=pI=p时，导向滤波就变成了边缘保持的滤波操作，此时原来求出的aa和bb的表达式就变成了：

ak=σ2kσ2k+ϵbk=(1−ak)μk

ak=σk2σk2+ϵbk=(1−ak)μk

考虑两种情况：

情况1：高方差区域，即表示图像II在窗口wkwk中变化比较大，此时我们有σ2k>>ϵσk2>>ϵ，于是有ak≈1ak≈1和bk≈0bk≈0。

情况2：平滑区域（方差不大），即图像II在窗口wkwk中基本保持固定，此时有σ2k<<ϵσk2<<ϵ，于是有ak≈0ak≈0和bk≈μkbk≈μk。

也就是说在方差比较大的区域，保持值不变，在平滑区域，使用临近像素平均（也就退化为普通均值滤波）。（这个思想跟文献【1】里设计的自适应降噪滤波器有异曲同工之妙，当然也不完全相同！）

上面的给出的是对灰度图像进行导向滤波的代码。你可能会好奇彩色图像该如何使用导向滤波。一个比较直接的方法就是将引导滤波分别应用到RGB三个颜色通道中，然后在组合成结果图像。更多细节可以参考作者原文。不仅如此，在本文开始我们也谈到，导向滤波不仅可以应用与图像平滑，还可以用于图像去雾、图像Matting等多个领域，限于篇幅我们无法一一详述，有兴趣的读者可以参考作者原文以了解导向滤波的其他应用。

最后，需要说明的是在新版的MATLAB中（R2014及以后），已经内置了用于导向滤波的函数imguidedfilter（而这个函数实现的其实是Fast Guided Filter），也就是说在实际开发中我们已经不再需要编写上面那样的代码，而是只要简单调用MATLAB的内置函数就可以了。