二进制转BCD码需要几步？——漫谈大四加三算法的Verilog实现

Hi，大家好！我是至芯科技的李老师。

今天讲课的题目比较有意思，它是一个小问题：把二进制变成BCD码需要几步？
请大家思考一下。有同学可能回答需要三步，为什么啊？
因为啊，把大象放进冰箱里需要三步，第一步，把冰箱门打开，第二步，把大象放进去，第三步，把冰箱门关上。
类似的，把二进制变成BCD码，也需要三步。
blablablabla ......
当然啦，这是开玩笑了。不过，歪打正着，答案确实是三步。
究竟是怎么回事呢？我们下面细细说来，原理说透之后，我们演示一下具体的Verilog实现过程。

首先，看一下下面这张表格，把二进制（8’hFF）转换为BCD（12’h255）的步骤列表。

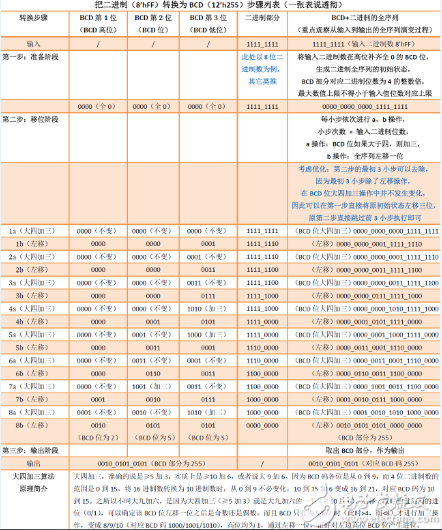
什么是二进制转BCD？有什么用？

4位二进制是16进制数，而生活中常用的数制是10进制数。
怎么样用计算机来理解、表达生活中的10进制数？这就需要进行16进制数与10进制数的相互转换了。
而BCD码（Binary-Coded Decimal）正是计算机常用的一种表达方式。
它是一种以二进制表示的十进制数码。
比如说，至芯科技ZX-1开发板上的六位数码管显示数字可以是16进制的000000~FFFFFF，但是更为方便的方法是000000~999999。
六位数码管显示六位数字用十六进制，比如说是0F423F，谁也不知道是多少，但是它对应的十进制数999999，大家肯定很熟悉。
很多场合，我们和机器之间沟通用10进制更方便，但计算机是用01编码的。需要进行人机之间的沟通和转换。
解决的方法就是用二进制的方式来存储、计算数值，但是用10进制的方式来显示这些数值，BCD码就起到了桥梁的作用。
注意，16进制属于二进制的一种形式，希望大家理解这点，包括8进制也是。

当然，道理容易明白。但究竟机器又是怎样实现二进制和BCD码的转换的呢？
注意，转换是双向的，既可以把二进制转换成BCD码，也可以把BCD码转换成二进制数。
可以想象BCD码转成二进制相对比较简单。
举个例子吧，比如说BCD码255，要转换成二进制。
计算机里面存的BCD码是12'h255（对应二进制为12'b0010_0101_0101），肯定不能直接进行运算，必须要转换成机器识别的二进制数值12'h0FF（对应二进制为12'b0000_1111_1111）。
先算前两位，直接2*10+5，得到结果25，然后再将结果*10+下一位，即25*10+5，最终结果为255，完了。
就这么简单。当然这里255只有三位BCD位，如果更多的话，以此类推。
将前一步结果*10+下一位，得到当前结果。
当然实现起来还有一些小的技巧，x*10要占用乘法器资源，如果乘法器资源足够那无所谓，但在资源有限的情况下通常用(x<<3)+(x<<1)（对应x*8+x*2）来实现。
即用移位和加法来代替乘法操作。
当然也可以把BCD数字的每一位直接变成各种左移数值的组合，比如x*100 = x*64 + x*32 * x*4 = (x<<6) +( x<<5) + (x<<2)。
上面就是BCD码转成二进制的实现原理，这个比较简单，我们这里略微带过。

本课重点讲解的是反过来怎么实现，即怎么把二进制转换成BCD码？
比如说，二进制数12'h0FF，要转换成BCD码255。
这个有点难，常见的做法是使用上图中提到的大四加三算法。
当然你可以用查表法，比如说256以内的数值，直接用查表的方式，一一对应，就像我们FPGA采用LUT表实现真值表那样，或者说用ROM表来根据不同输入得到不同输出。
这样当然也是可以的，不过，它的范围往往比较有限，不适于数量比较大的情况。

下面，我们就隆重有请本次课堂的主角——大四加三算法，隆重登场。

大四加三算法

如果前面那张表格，大家能看懂的话，我们就可以直入主题了。
从表中我们可以看到，把二进制变成BCD码，也需要三步。

首先，明白问题的输入和输出要求，这是最起码的，即输入二进制数（比如8’hFF），要求输出对应的BCD码（对应为BCD码12'h255）。
大四加三算法就是实现的过程。

第一步：准备阶段。
我们将输入二进制数在高位补齐全0的BCD位，生成二进制全序列的初始状态。
BCD部分对应二进制位数为4的整数倍，最大数值上限不得小于输入值位数对应上限。

第二步：移位阶段。
第二步比较复杂。这一步分为多个小步，每小步将二进制全序列进行一次组合的左移操作。
之所以称之为组合的左移操作，是因为包括一次移位的预操作（即BCD位大四加三）和单纯的全序列左移操作。
具体这一步的操作过程，我们后面还会细讲。
实际上大象那个比喻，也是第二步比较复杂。呵呵。
一旦原理明白了，我们编写Verilog代码想必也就水到渠成了。后面就是Verilog语言练习和具体实现的事了。

第三步：输出阶段。
这一步，最简单，实际上第二步的最后环节已经得出结果了，只不过它包含在全序列里面，我们只要取出需要的BCD部分，输出即可。

大四加三算法原理简介

我们再回到第二步上来，实质上也是大四加三算法上来。
第一步、第三步就是准备和结束的阶段，等同于打开冰箱门、关闭冰箱门。重点还是在于大象怎么放到冰箱里的。

第二步里面分为多个小步，每小步依次进行a、b操作，小步次数 = 输入二进制位数。
a操作：BCD位如果大于四，则加三。
b操作：全序列左移一位。

大四加三，准确的说是≥5加3，实质上是≥10加6，或者说大9加6。
因为BCD码各位是从0到9，而4位二进制数的范围是0到15，将16进制数转换为10进制数时，从0到9不必变化，10到15加6变成16到21，对应BCD码为10到15。
之所以不叫大九加六，是因为大四加三（≥5加3）就是大九加六的一半（≥10加6），左移一位时通过后面的进位（0/1），可以确定该BCD位左移一位之后是奇数还是偶数。
而且BCD只有为5/6/7时（此时>4，而<8）才进行加三操作，变成8/9/10（对应BCD码1000/1001/1010），高位均为1，通过左移一位，正好对左边高位BCD位产生进位。

这样说有点抽象，那张表格如果大家没有一步步演变清楚的话，可以先弄清楚了。这样有助于理解这个算法。
当然这个算法严谨的证明过程肯定也是有的，李凡老师也提到过，有兴趣的话可以深入钻研一下。
这里，我们就先用归纳的方法，检验这种算法确实是能一步步将二进制数转换成BCD码。
表中输入的是8位二进制数，位数更多，实质上原理是一样的，每位之间的递进关系是2倍，每四位之间的递进关系是16倍，你在增加位数，递进的关系都是一样的。
当然我们也可以自己推导一下12位二进制数，或者更多位，满足一下我们的好奇心和求知欲。
就像图示的表格一样，只不过位数增加了而已。

本堂课要解决的课题

原理讲过之后，我们要做一个更多位数的例子。
也就是开发板六位数码管显示的的问题，我们让六位数码管循环显示十进制数000000~999999。

十进制数000000~999999在计算机里面，用于显示实际上是BCD码000000~999999，而用于计算处理则是二进制数20'h00000~20'hF423F（对应20'd0~20'd99999）。
在循环显示的时候，我们控制部分要对计数器进行加一操作，这时候是对二进制数进行操作。
在显示输出的时候，我们将二进制数转换为BCD码，输出给数码管进行显示。这时候，就用到了二进制数转换为BCD码的操作，也就是大四加三算法。
所以说，这个例子对大四加三算法模块的输入输出要求是，输入20位的二进制数20'h00000~20'hF423F（对应20'd0~20'd99999），要求输出对应的6位BCD码000000~999999，对应二进制位数是24位。
显然这里的20位输入24位输出，比表格中的8位输入12位输出要多了很多，当然我们不是手工推导，而是要用FPGA来做，用Verilog代码来建模。

建模主体框架 首先建立工程文件夹b2bcd，编写顶层模块b2bcd.v文件。 module b2bcd (din, dout); input [19:0] din; output [23:0] dout; wire [43:0] data [20:0]; assign data[0] = {24'b0, din}; //第一步：准备阶段。将输入二进制数在高位补齐全0的BCD位，生成二进制全序列的初始状态。 shift s01 (.datain(data[0]), .dataout(data[1])); //第二步：移位阶段。依次进行20个小步操作。具体动作在shift子模块中描述。 shift s02 (.datain(data[1]), .dataout(data[2])); shift s03 (.datain(data[2]), .dataout(data[3])); shift s04 (.datain(data[3]), .dataout(data[4])); shift s05 (.datain(data[4]), .dataout(data[5])); shift s06 (.datain(data[5]), .dataout(data[6])); shift s07 (.datain(data[6]), .dataout(data[7])); shift s08 (.datain(data[7]), .dataout(data[8])); shift s09 (.datain(data[8]), .dataout(data[9])); shift s10 (.datain(data[9]), .dataout(data[10])); shift s11 (.datain(data[10]), .dataout(data[11])); shift s12 (.datain(data[11]), .dataout(data[12])); shift s13 (.datain(data[12]), .dataout(data[13])); shift s14 (.datain(data[13]), .dataout(data[14])); shift s15 (.datain(data[14]), .dataout(data[15])); shift s16 (.datain(data[15]), .dataout(data[16])); shift s17 (.datain(data[16]), .dataout(data[17])); shift s18 (.datain(data[17]), .dataout(data[18])); shift s19 (.datain(data[18]), .dataout(data[19])); shift s20 (.datain(data[19]), .dataout(data[20])); assign dout = data[20][43:20]; //第三步：输出阶段。取出BCD部分，作为输出。 endmodule

b2bcd.v文件

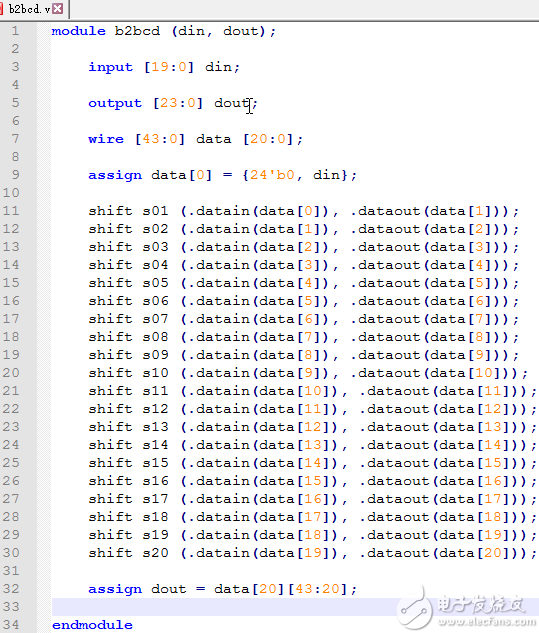
建模shift移位子模块

shift移位子模块shift.v文件如下：

module shift (datain, dataout);

input [43:0] datain;

output [43:0] dataout;

wire [43:0] data;

assign data[19:0] = datain[19:0];

preshift p0 (.d4in(datain[23:20]), .d4out(data[23:20])); //对应第二步各小步下的a操作，此处为6个BCD位的大四加三操作。具体动作见preshift移位预操作子模块。
preshift p1 (.d4in(datain[27:24]), .d4out(data[27:24]));
preshift p2 (.d4in(datain[31:28]), .d4out(data[31:28]));
preshift p3 (.d4in(datain[35:32]), .d4out(data[35:32]));
preshift p4 (.d4in(datain[39:36]), .d4out(data[39:36]));
preshift p5 (.d4in(datain[43:40]), .d4out(data[43:40]));

assign dataout = {data[42:0], 1'b0}; //对应第二步各小步下的b操作，此处为全序列的左移移位操作。

endmodule

shift子模块shift.v

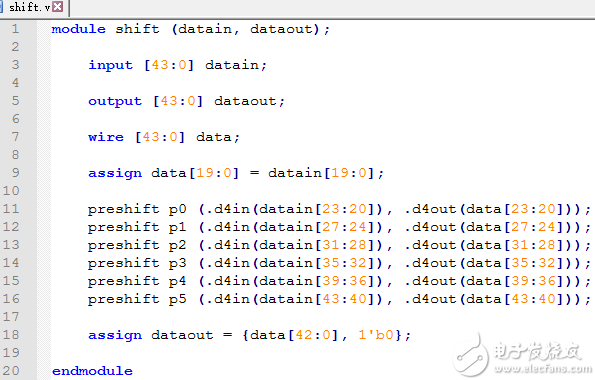
建模preshift预移位操作子模块

preshift预移位操作子模块preshift.v文件如下：

module preshift (d4in, d4out);

input [3:0] d4in;

output reg [3:0] d4out;

always @ (*)
begin
if (d4in > 4)
begin
d4out = d4in + 3; //如果大于四，则加三
end
else
begin
d4out = d4in; //如果不大于四，则不变
end
end

endmodule

preshift预移位操作子模块preshift.v

preshift预移位操作子模块，也可以这样写

module preshift (d4in, d4out);

input [3:0] d4in;

output [3:0] d4out;

assign d4out = (d4in > 4) ? d4in + 4'd3 : d4in; //如果大于四，则加三，否则不变。

// always (*)
// begin
// if (d4in > 4)
// begin
// d4out = d4in + 3;
// end
// else
// begin
// d4out = d4in;
// end
// end

endmodule

preshift预移位操作子模块的另一种写法

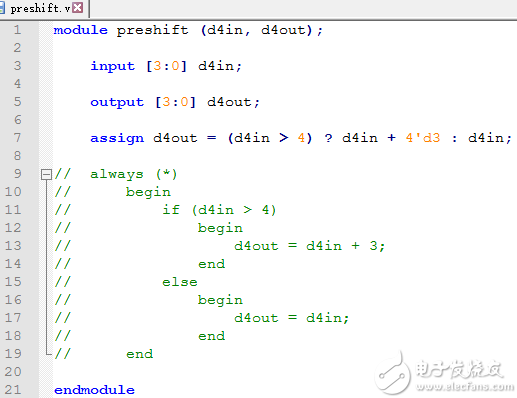
编写Testbench模块


Testbench模块b2bcd_tb.v文件如下：

`timescale 1ns/1ps

module b2bcd_tb;

reg [19:0] din;

wire [23:0] dout;

integer i;

b2bcd dut (.din(din), .dout(dout));

initial
begin
din = 0;
for (i=0; i<=999999; i=i+1) #10 din = i;                //六位数码管循环显示000000~999999

#100 $stop;
end

endmodule

Testbench模块b2bcd_tb.v文件

仿真运行结果

设置好仿真之后，可以看到仿真结果。
此时将din的数据格式设置为无符号数Unsigned，将dout的数据格式设置为十六进制数Hexadecimal。
可以看到两种不同码制的数据保持了完全一致。
从一个方面验证了大四加三算法的正确性。

仿真运行结果图示

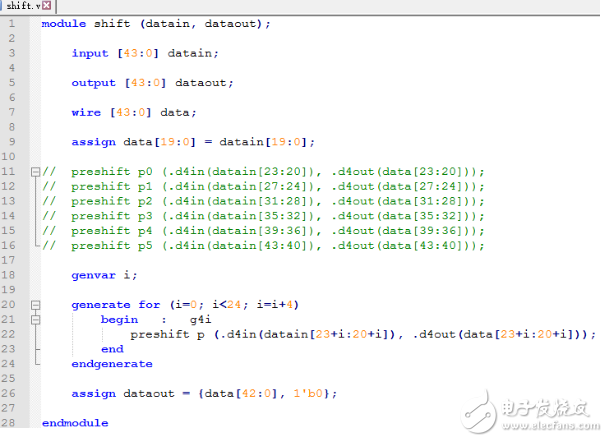
用generate for语句改写shift移位子模块shift.v文件

我们注意到由于存在重复性操作，相同的语句往往写好多次。当然参数会稍微有所差异。
有个偷懒的办法，就是采用generate for语句。
用generate for语句改写的shift移位子模块shift.v文件如下所示：

module shift (datain, dataout);

input [43:0] datain;

output [43:0] dataout;

wire [43:0] data;

assign data[19:0] = datain[19:0];

// preshift p0 (.d4in(datain[23:20]), .d4out(data[23:20]));
// preshift p1 (.d4in(datain[27:24]), .d4out(data[27:24]));
// preshift p2 (.d4in(datain[31:28]), .d4out(data[31:28]));
// preshift p3 (.d4in(datain[35:32]), .d4out(data[35:32]));
// preshift p4 (.d4in(datain[39:36]), .d4out(data[39:36]));
// preshift p5 (.d4in(datain[43:40]), .d4out(data[43:40]));

genvar i;

generate for (i=0; i<24; i=i+4)
begin : g4i
preshift p (.d4in(datain[23+i:20+i]), .d4out(data[23+i:20+i])); //对应第二步各小步下的a操作，此处为6个BCD位的大四加三操作。具体动作见preshift移位预操作子模块。
end
endgenerate

assign dataout = {data[42:0], 1'b0}; //对应第二步各小步下的b操作，此处为全序列的左移移位操作。

endmodule

用generate for语句改写的shift移位子模块shift.v文件

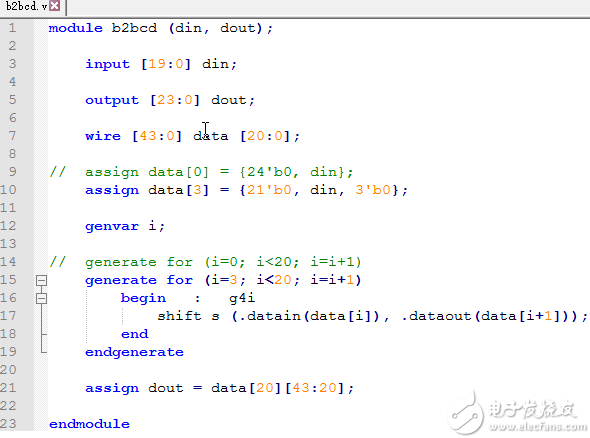
用generate for语句改写顶层模块b2bcd.v文件

同样的道理，我们对顶层模块b2bcd.v文件的重复性语句也进行了改写。
用generate for语句改写的顶层模块b2bcd.v文件如下所示：

module b2bcd (din, dout);

input [19:0] din;

output [23:0] dout;

wire [43:0] data [20:0];

assign data[0] = {24'b0, din}; //第一步：准备阶段。将输入二进制数在高位补齐全0的BCD位，生成二进制全序列的初始状态。

genvar i;

generate for (i=0; i<20; i=i+1)
begin : g4i
shift s (.datain(data), .dataout(data[i+1])); //第二步：移位阶段。依次进行20个小步操作。具体动作在shift子模块中描述。
end
endgenerate

assign dout = data[20][43:20]; //第三步：输出阶段。取出BCD部分，作为输出。

endmodule

第二步的小步次数优化

前面表格中我们提到，第二步的最初3小步可以去除，因为最初3小步除了左移操作，在BCD位大四加三操作中并不发生变化。
因此可以在第一步直接将原初始状态左移三位，原第二步直接跳过前3小步执行即可。
优化结果体现在顶层模块b2bcd.v文件中，如下所示：

module b2bcd (din, dout);

input [19:0] din;

output [23:0] dout;

wire [43:0] data [20:0];

// assign data[0] = {24'b0, din};
assign data[3] = {21'b0, din, 3'b0}; //第一步：准备阶段。将输入二进制数在高位补齐全0的BCD位，直接左移三位，生成二进制全序列的初始状态。

genvar i;

// generate for (i=0; i<20; i=i+1)
generate for (i=3; i<20; i=i+1)
begin : g4i
shift s (.datain(data), .dataout(data[i+1])); //第二步：移位阶段。依次进行17个（20-3）小步操作。具体动作在shift子模块中描述。
end
endgenerate

assign dout = data[20][43:20]; //第三步：输出阶段。取出BCD部分，作为输出。

endmodule

第二步的小步次数优化结果体现在顶层模块b2bcd.v文件中

查看RTL视图——顶层模块b2bcd.v


顶层模块b2bcd.v的视图如下所示。
其中最下面为全局视图，上面为左边、右边的局部视图，可以看到17个子步shift移位模块逐次递进的一个结果。

17个子步shift移位模块逐次递进的RTL视图

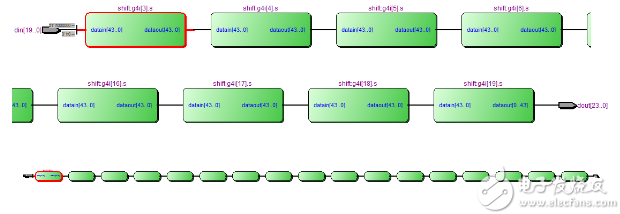
shift移位子模块shift.v的RTL视图如下。

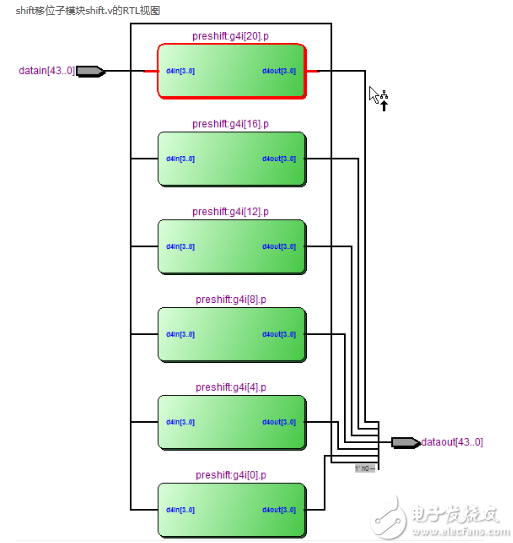
preshift移位预操作子模块preshift.v的RTL视图

 

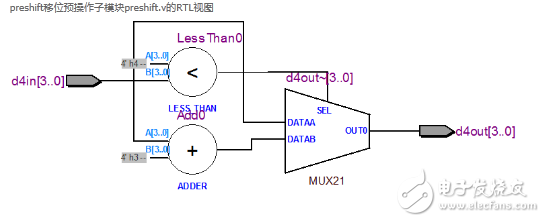
加入数码管驱动模块seg7.v文件

为了更直观地看到数码管显示效果，在已经做好的工程文件中加入编写好的数码管驱动模块seg7.v文件。
数码管驱动模块seg7.v文件如下所示。

module seg7 (clk, rst_n, data, sel, seg);

input clk, rst_n;
input [23:0] data;

output reg [2:0] sel;
output reg [7:0] seg;


reg [19:0] count;
reg clk_1ms;

always @ (posedge clk or negedge rst_n)
begin
if (!rst_n)
begin
clk_1ms <= 1;
end
else
begin
if (count < 24999)
begin
count <= count + 20'd1;
end
else
begin
count <= 0;
clk_1ms <= ~clk_1ms;
end
end
end


reg [2:0] state;
reg [3:0] data_temp;

always @ (posedge clk_1ms or negedge rst_n)
begin
if (!rst_n)
begin
sel <= 0;
data_temp <= 0;
state <= 0;
end
else
begin
case (state)
0 : begin
sel <= 0;
data_temp <= data[23:20];
state <= 1;
end

1 : begin
sel <= 1;
data_temp <= data[19:16];
state <= 2;
end

2 : begin
sel <= 2;
data_temp <= data[15:12];
state <= 3;
end

3 : begin
sel <= 3;
data_temp <= data[11:8];
state <= 4;
end

4 : begin
sel <= 4;
data_temp <= data[7:4];
state <= 5;
end

5 : begin
sel <= 5;
data_temp <= data[3:0];
state <= 0;
end

default : state <= 0;

endcase
end
end


always @ (*)
begin

if (!rst_n)
begin
seg = 8'b1111_1111;
end
else
begin
case (data_temp)
0 : seg = 8'b1100_0000; //d0
1 : seg = 8'b1111_1001; //d1
2 : seg = 8'b1010_0100; //d2
3 : seg = 8'b1011_0000; //d3
4 : seg = 8'b1001_1001; //d4
5 : seg = 8'b1001_0010; //d5
6 : seg = 8'b1000_0010; //d6
7 : seg = 8'b1111_1000; //d7
8 : seg = 8'b1000_0000; //d8
9 : seg = 8'b1001_0000; //d9
10 : seg = 8'b1000_1000; //dA
11 : seg = 8'b1000_0011; //db
12 : seg = 8'b1100_0110; //dC
13 : seg = 8'b1010_0001; //dd
14 : seg = 8'b1000_0110; //dE
15 : seg = 8'b1000_1110; //dF
default : seg = 8'b1000_1110; //dF
endcase
end
end

endmodule

创建新的顶层模块top.v

创建新的顶层模块top.v，循环生成要显示的数字000000~999999，显示数字每100ms更新一次，通过b2bcd模块转换成BCD码，然后输出给数码管驱动模块。
新的顶层模块top.v文件如下所示。

module top (clk, rst_n, sel, seg);

input clk, rst_n;

output [2:0] sel;
output [7:0] seg;


reg [31:0] count;
reg [19:0] din;

wire [23:0] dout;

parameter T100ms = 5_000_000;

always @ (posedge clk or negedge rst_n)
begin
if (!rst_n)
begin
count <= 0;
din <= 0;
end
else
begin
if (count < T100ms - 1)                                //显示数字每100ms更新一次
begin
count <= count + 1;
end
else
begin

count <= 0;
if (din < 999999)                                //循环生成要显示的数字000000~999999
begin
din <= din + 20'd1;
end
else
begin
din <= 0;
end
end
end
end

b2bcd b2bcd
(
.din(din),
.dout(dout)
);

seg7 seg7
(
.clk(clk),
.rst_n(rst_n),
.data(dout),
.sel(sel),
.seg(seg)
);


endmodule

参照.tcl文件设置好FPGA管脚


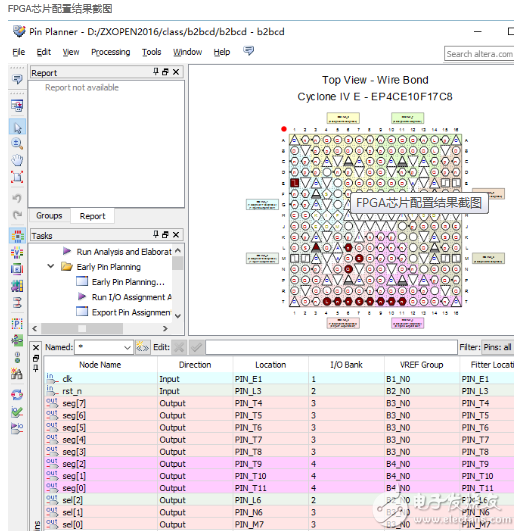
参照EP4CE10F17C8Nzx_1.tcl文件内容，对FPGA芯片管脚进行设置。

EP4CE10F17C8Nzx_1.tcl文件相关内容如下所示。FPGA芯片配置结果如图所示。

#set_global_assignment -name FAMILY "Cyclone IV"
#set_global_assignment -name DEVICE ep4ce10f17c8n

set_location_assignment PIN_E1 -to clk

# KEY 轻触按键
set_location_assignment PIN_L3 -to key[0]

# SEG7 x 8 七段数码管
set_location_assignment PIN_L6 -to sel[2]
set_location_assignment PIN_N6 -to sel[1]
set_location_assignment PIN_M7 -to sel[0]
set_location_assignment PIN_T11 -to seg[0]
set_location_assignment PIN_T10 -to seg[1]
set_location_assignment PIN_T9 -to seg[2]
set_location_assignment PIN_T8 -to seg[3]
set_location_assignment PIN_T7 -to seg[4]
set_location_assignment PIN_T6 -to seg[5]
set_location_assignment PIN_T5 -to seg[6]
set_location_assignment PIN_T4 -to seg[7]

FPGA芯片配置结果截图

.sof文件下载到FPGA


全编译FPGA工程，生成.sof文件，连接至芯ZX-1开发板并上电。
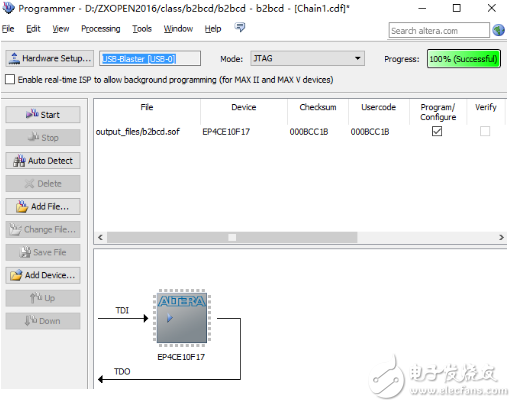
打开Programmer通过Jtag口，将.sof文件下载到FPGA进行在线仿真。
.sof文件下载界面如下图所示。

开发板运行效果

开发板运行效果如下图所示。
经检查，开发板运行效果与设计相符。

课程小结

本节课带领大家学习了二进制转换成BCD码的原理，并使用Verilog实现大四加三算法的建模，结合六位数码管显示，在至芯ZX-1开发板上演示了程序结果。
希望大家通过本次课程的学习，掌握大四加三算法的原理，熟练编写相关FPGA工程，掌握Verilog语法和相关开发工具。
课程到此结束，谢谢大家观赏。