普及一下程序猿们经常遇见的树

公历 3 月 12 日是一年一度的植树节。旨在宣传保护森林，并动员群众参加植树造林活动。说到树，程序猿们肯定不陌生，趁着这个植树节，普及一下程序猿们经常遇见的树。

二叉搜索树

定义

二叉搜索树又称二叉查找树，亦称为二叉排序树。设 x 为二叉查找树中的一个节点，x 节点包含关键字 key，节点x 的 key 值记为 key[x] 。如果 y 是 x 的左子树中的一个节点，则 key[y] <= key[x] ；如果 y 是 x 的右子树的一个节点，则 key[y] >= key[x] 。

查找性能

当数据数目为 N，树高度保持 logN 附近。则平均查找长度与 logN 成正比，查找平均时间复杂度为 O(logN) 。 当先后插入的关键字有序时，二叉搜索树退化成单支树结构。此时树高 N 。平均查找长度为 (N+1)/2 ，查找的平均时间复杂度为 O(N) 。

插入性能

插入效率与查找效率一致。  

删除性能

删除节点时，若节点为叶子节点，或者节点只有单一子树，则时间复杂度为 O(1) 。若节点既有左子树又有右子树，则需要执行递归过程，对应时间复杂度为 O(logN) 。

应用场景

二叉排序树就既有链表的好处，也有数组的好处，因此在处理大批量的动态的数据是比较有用。

种树

平衡二叉树

定义

平衡二叉树是一种特殊的二叉搜索树。平衡二叉树保证节点平衡因子的绝对值不超过1，保证了树的平衡。

查找性能

平衡二叉树是严格平衡的，那么查找过程与二叉搜索树一样，只是平衡二叉树不会出现最差的单支树情形。因此查找效率最好，最坏情况时间复杂度为 O(logN) 。

插入性能

插入数据之前需要进行查找操作，查找到插入位置。插入数据后需要进行旋转操作，旋转操作复杂度为常量级。因此插入数据的时间复杂度与查找相同为 O(logN)。

删除性能

删除数据同样需要查找数据，在删除数据后需要进行调整。一次删除最多需要需要O(logN)次旋转，因此删除数据的时间复杂度为O(logN)+O(logN)=O(2logN)。

应用场景

SGI/STL的 set/map 底层都是用红黑树（平衡二叉树的一种）实现的。

种树

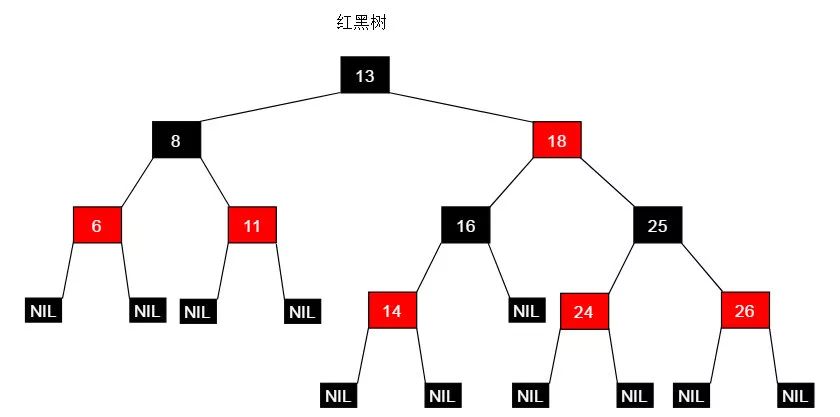
红黑树

定义

平衡二叉树的严格平衡策略以牺牲建立查找结构(插入，删除操作)的代价，换来了稳定的O(logN) 的查找时间复杂度。红黑树采用了折中策略，即不牺牲太大的建立查找结构的代价，同时又能保证稳定高效的查找效率。

查找性能

由于红黑树的性质(最长路径长度不超过最短路径长度的 2 倍)，可以说明红黑树虽然不像平衡二叉树一样是严格平衡的，但平衡性能还是要比二叉搜索树要好。其查找代价基本维持在 O(logN) 左右，但在最差情况下(最长路径是最短路径的 2 倍少 1)，比平衡二叉树效率低一些。

插入性能

红黑树插入结点时，需要旋转操作和变色操作。但由于只需要保证红黑树基本平衡就可以了。因此插入结点最多只需要2次旋转，这一点和平衡二叉树的插入操作一样，但是变色操作的时间复杂度为O(logN)。

删除性能

红黑树的删除操作代价要比平衡二叉树要好的多，删除一个结点最多只需要 3 次旋转操作，保证了删除时间复杂度维持在常量级。

应用场景

应用场景有很多。

Java 中的 TreeSet ,TreeMap，HashMap

C++ 的 STL中的 map 和 set 都是用红黑树实现的

epoll 在内核中的实现，用红黑树管理事件块

nginx 中，用红黑树管理 timer 等

linux 进程调度 Completely Fair Schedule r,用红黑树管理进程控制块

种树

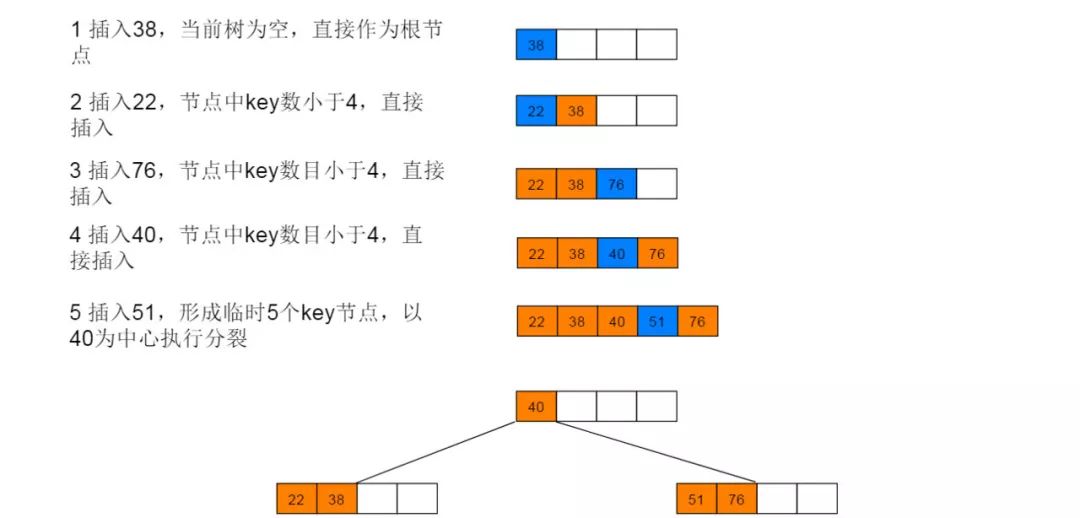
B 树

定义

B树是一种多路平衡查找树，在相同数据数目情形下，B树的高度更小，这样就减少了磁盘的IO次数，在文件系统以及数据库索引等场景下提升了查找效率。

查找性能

B树的查找分成两种：一种是从一个结点查找另一结点的地址的时候，需要定位磁盘地址(查找地址)，查找代价极高。另一种是将结点中的有序关键字序列放入内存，进行优化查找(可以用折半)，相比查找代价极低。而B树的高度很小，因此在这一背景下，B树比任何二叉结构查找树的效率都要高很多。

插入性能

B树的插入会发生结点的分裂操作。当插入操作引起了 s 个节点的分裂时，磁盘访问的次数为 h (读取搜索路径上的节点) ＋2s (回写两个分裂出的新节点) ＋1（回写新的根节点或插入后没有导致分裂的节点）。因此，所需要的磁盘访问次数是 h+2s+1，最多可达到 3h+1。因此插入的代价较大。

删除性能

B树的删除会发生结点合并操作。最坏情况下磁盘访问次数是 3h＝（找到包含被删除元素需要h次读访问）+（获取第2至h层的最相邻兄弟需要h-1次读访问）+（在第3至h层的合并需要h-2次写访问）+（对修改过的根节点和第2层的两个节点进行3次写访问）。

应用场景

B树/B+树主要用于磁盘文件组织 数据索引和数据库索引等场景。

种树

B+ 树

定义

B+树是B-树的一种变体，B+树相比B-树的特点：

（1）索引节点的key值均会出现在叶子节点中。（2）索引节点中的key值在叶子节点中或者为最大值或者为最小值。（3）叶子节点使用单链表的形式链接起来。

查找性能

（1）在相同数量的待查数据下，B+树查找过程中需要调用的磁盘IO操作要少于普通B-树。由于B+树所在的磁盘存储背景下，因此B+树的查找性能要好于B-树。

（2）B+树的查找效率更加稳定，因为所有叶子结点都处于同一层中，而且查找所有关键字都必须走完从根结点到叶子结点的全部历程。因此同一颗B+树中，任何关键字的查找比较次数都是一样的。而B树的查找是不稳定的。

插入性能

B+树的插入过程与B树类似，性能也基本一致。

删除性能

删除性能与B树也基本一致。

应用场景

B树/B+树主要用于磁盘文件组织 数据索引和数据库索引等场景。

种树

霍夫曼树

定义

给定 n 个权值作为 n 个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为霍夫曼树(Huffman Tree)。

霍夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

应用场景

霍夫曼树主要用于霍夫曼编码，进行数据压缩领域。

霍夫曼编码