梯度下降算法在深度学习中扮演着举足轻重的地位

老伙计梯度下降算法在深度学习中扮演着举足轻重的地位，今天我们来从另一个角度来看这个算法的推演。

我们知道，对于一个足够光滑的函数，大一时候学过的泰勒展开公式告诉我们，在已知该函数在某一点的各阶导数值的情况之下，可以用这些导数值做系数构建一个多项式来近似函数在这一点的邻域中的值。于是，对于一个损失函数函数g(w)，我们现在知道它在w0处的函数值以及各阶导数值，如何从w0出发来找到g(w)的极小值呢？我们可以对g(w)在w0点处展开，只保留到一阶导数，得到如下公式（其中▽表示梯度）：

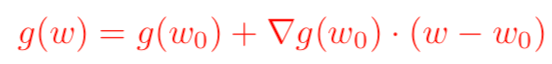
需要注意的是，泰勒公式是一个近似表达式，若w距离w0越近，则近似效果越准确；反过来，若w偏离w0较大，那么近似效果就会比较差。因此，我们在用上式来代表g(w)的时候，应该遵守一个约束条件，这个约束是w距离w0的距离要足够小。我们可以用距离公式，表示距离的公式有很多，使用最常见的欧几里得距离公式，并且为了接下来求导方便，加上一个系数1/(2*lr)在前面，于是寻找g(w)的最小值就变成了对下面表达式求关于w的梯度：

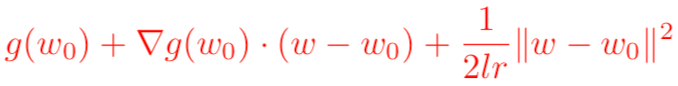
求完梯度之后并设置其等于0，即可得到我们非常熟悉的梯度下降算法的原始公式：

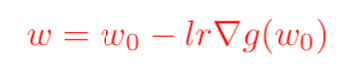
这里的欧几里得距离公式也可以换成其他距离公式（下文延伸分享其他距离公式）。这同样也解释了，我们为什么有时候在损失函数里面加上一个L2损失函数会更好，这样可以防止梯度更新步幅过大，进而引发损失值发生剧烈的抖动。

延伸：

距离表示的是一个集合中不同元素远近的度量，当距离为0的时候表示这两个元素是相同的。数学中，我们学过的距离主要有以下几种：

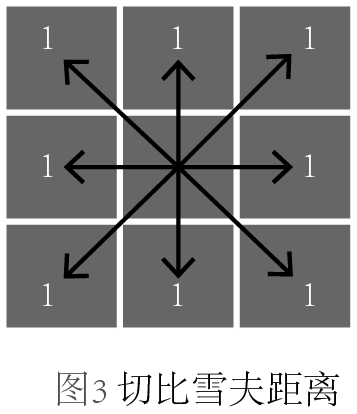
上氏中，当p取不同值得时候，又可以细分为不同的距离，当p=1，称为曼哈顿距离；当p=2，称为欧几里得距离；当p=∞，称为切比雪夫距离。我们不禁要问，它们的区别是什么？为了更形象地展示它们，我画了三幅图来区分，每幅图中箭头表示的是从中心点到各个格子中心点的度量：

图1，曼哈顿距离，它是所有坐标轴差值的求和，可以想象一个城市的街道是完全网格状的，那么你从一个地方走到另一个地方就必须得走成曼哈顿距离的形状。

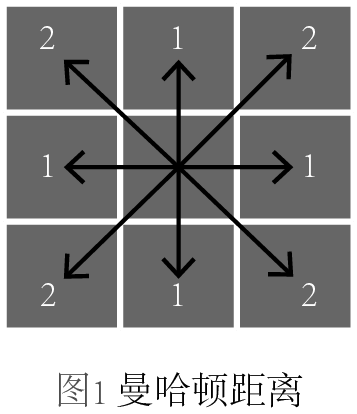
图2，欧几里得距离，这种距离是最常见的，勾股定理中用的就是这种距离。

图3，切比雪夫距离，各个坐标轴差值的最大值。

明可夫斯基距离，又称明氏距离，是一个定义在赋范空间的距离，赋范空间是指一个由范数构成的向量空间，明氏距离具有平移不变性和同质性，它的公式如下：

除了明氏距离之外，我们在自然语言处理中还用过余弦距离，通常余弦距离是用来判断两个元素的相似度（例如文档或段落），我们可以通过如下公式来得到余弦距离的计算：

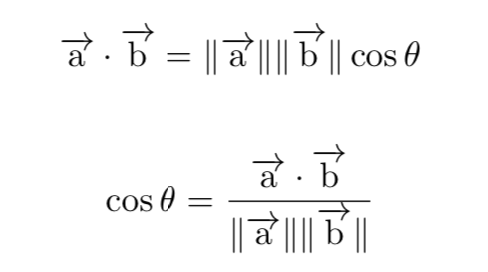
由此可见我们只关心两个向量的方向是否一致，而并不关心它们各自的幅度。当余弦值为1的时候，代表两个方向完全一致，即有相似性；当余弦值为0的时候，代表两个方向正交，可能只有少量相似性；当余弦值为-1的时候，方向完全相反，没有相似性。

还有一种距离也蛮常见，叫做马氏距离，它是衡量一个点到一个分布之间的距离，或者说偏离程度。给定分布的均值μ和协方差S，从点x到该分布的马氏距离的计算公式如下：

以上就是我们常见的距离及其表达式。