摘要:佛说:“一花一世界、一叶一菩提”,说的是寻常细微之物中有大千世界的缩影,我们可以从中知微见著。而如果从系统科学的视角,这话可以解出新意。微观来说,基本粒子组成了中子、质子和电子,又组成各类元素,元素组成了水、蛋白质、脂类、糖类与无机盐等化合物,化合物组成了细胞,细胞组成了一花一叶,世间万物,概莫如是,这便是系统自组织的过程。
人们研究系统科学,就是要探寻系统的组织与演化规律,以耗散结构、协同学、突变论为代表的系统自组织理论对系统演化规律进行了定性的解读,但缺少数学的参与,任何理论方向都不能称之为成熟。本篇介绍的系统科学的非线性理论,包括分形与混沌,是从几何与代数方面去探寻复杂系统的演化规律,而复杂适应系统理论,则是从更大规模,更长时间尺度上去探寻系统的演化规律,可以说,系统科学发展到当前阶段,离把握系统演化过程的本质又近了一步。
自相似
人们一定惊叹于自然界中事物外在形态几何图形的千变万化,但在这变化之中却有着一种神奇的性质,自相似性。无论是植物、动物、物理现象还是地形地貌,都能找到不胜枚举的自相似的对象,包括人体的血管、肺部、神经系统等的构造上也具有高度的自相似性。举几个简单例子,如下图中的松果、花椰菜的外形,还有闪电的纹路,都是典型的自相似现象。无机世界中因为物理规律是相同的,所以闪电、地形地貌、海岸线等具有自相似性很好理解,而有机生命体在自我复制过程中受到相同的基因组控制,也必然会出现大量相同的迭代过程,从而出现自相似性,只是生命体在有限空间内,不是无限扩张,而是实现了对迭代的极限收敛,于是出现了按比例的逐渐缩小,以致极限的现象,这正是生命体的奇妙之处。
自然界的这种神奇的自相似特性被艺术家们发现,体现在了艺术创作上,达到了独特的艺术效果。其中的代表人物就是荷兰版画家埃舍尔。埃舍尔以其绘画中的蕴含的数学性而闻名,美国人工智能领域先驱者之一侯世达,更是将埃舍尔的名字放进了他的书名之中,叫《哥德尔、埃舍尔、巴赫——集异璧之大成》,书中对埃舍尔画中体现的自相似、迭代与无穷的概念进行了阐述。下图是埃舍尔的两幅典型的自相似概念相关的版画。
20世纪初,自相似概念终于被数学家们所发现并利用,构造出了令人惊奇的曲线,有代表性的是科赫曲线和谢尔宾斯基三角形。他们有几个共同的性质:1)整体上处处不规则;2)不同尺度上,图形具有自相似性;3)都通过简单规则逐次迭代产生。这些曲线成为传统几何学中的怪物,无法用传统的几何学方法去解释,如科赫曲线,如果从一维的长度上去度量,是无穷长的。这些几何图形的性质困扰了几何学家们很长的时间,直到一个叫本华.曼德勃罗的美国数学家出现,他把这种几何上的自相似性发展了一门新的几何门类,即分形。
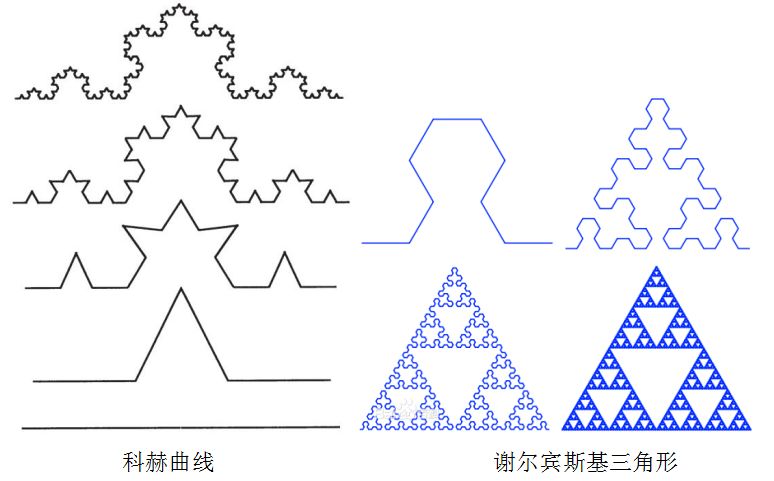
分形
曼德勃罗被称为分形之父,1967年,他发表了题为《英国的海岸线有多长?统计自相似和分数维度》的文章,提出采用不同度量标来测量,每次会得出完全不同的结果,尺度越小,测量的结果就会越长,并不会趋向于一个有限固定的结果。1975年曼德勃罗出版了《大自然的分形几何学》,奠定了分形理论的数学基础。而曼德勃罗以他的理论构建的“曼德勃罗集”被称为人类有史以来最奇异、最瑰丽的集合图形,被称为“上帝的指纹”。
曼德勃罗集
曼德勃罗集产生自一个简单的非线性迭代公式:
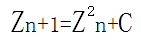
其中Z与C表示复数,代表了平面上的点,因为是平方运算,所以是非线性的。分形理论引种是对不规则的自然界的数学描述方法,因此又被称为描述大自然的几何学。
三体与混沌
《道德经》上说,道生一,一生二,二生三,三生万物。三是一个特别的数字,万物都孕育在三的变化当中。刘慈欣获得雨果奖的著名小说《三体》描述的三体世界中,也因为存在三个太阳而使得行星的轨迹无法精确求解,从而造成了三体世界的苦难。历史上三体问题本身就是一个经典问题。自从牛顿提出万有引力定律后,两个天体的运动规律问题得到解决,但多个天体的运动问题依然存在,哪怕只是三体问题。1887年瑞典国王发布了一笔奖金,征求4个难题的解答,其中就包括太阳系的稳定问题。奖金被当时的法国数学家庞加莱得到。他虽然没有彻底解决这个问题,但他提出了限制性三体问题的解决思路,所谓限制性三体问题,就是假设一个天体的质量比其它两个天体小很多,可忽略不计,从而其它两大天体的二体问题能够精确求解,大天体1与大天体2相对做椭圆轨迹运动。虽然如此,得到的第三个天体的运动轨迹依然是杂乱的,但是它又不会超出一定的空间范围,就好比杂乱之中又蕴含着某种程度的有序,这其实就是我们今天提到的“混沌”,只是当时人们还未认识到。这样就一定程度上说明了太阳系中太阳、地球和月球的稳定性,庞加莱获得了该项奖金。
2019年1月3日,我国嫦娥四号月球登陆车登陆月球成功,并且在世界上第一次实现了月球背面登陆,嫦娥四号登月的功臣们还得到了习主席的接见。由于月球背面总是背对着地球,无法实现登陆器与地球控制中心的通信,因此实现月球背面登陆是一个世界级难题,我国科学家们充分发挥了中国人民的智慧,想出了首先发射一个通信中继星的妙招,这就是“鹊桥”号中继星。“鹊桥”号中继星正好定位在地、月朗格朗日L2点上,这其中就用到了限制性三体问题的原理,地球、月球和“鹊桥”号中继星三者构成了限制性三体,法国数学家朗格朗日曾证明过限制性三体共存在5个动态平衡点,小质量天体在这五个地方可保持引力的平衡。我国科学家们选择了其中的朗格朗日L2点作为中继星的布放位置,当中继星到达L2点后,被地球和月球的引力所捕获,达到了引力的动态平衡。
5个拉格朗日点
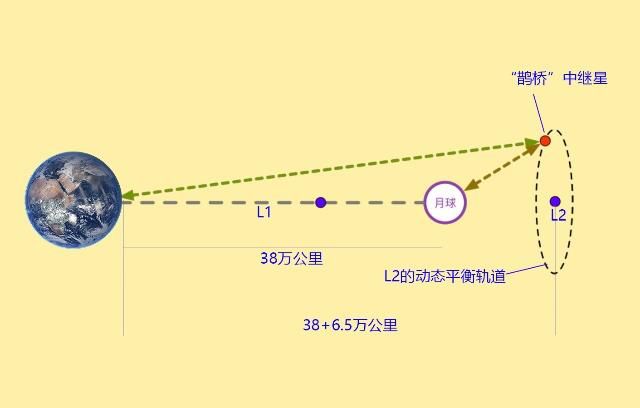
“鹊桥”中继星位于拉格朗日L2点位置
混沌
人们一提混沌,必须讲到美国气象学家洛伦茨以及他提出来的蝴蝶效应与奇异吸引子。1963年,气象学家洛伦茨在实验室研究气象预报模型时,稍微修改输入的值,得到了变化非常大的输出结果。按常理,确定性方程的结果应该是渐变的,稍微修改输入,输出变化应该不大才对,这样人们才能预测系统后续的行为。他输入的数据只差了0.000127,而这么微小差异却造成了结果的天壤之别,不服输的洛伦茨把大量的实验结果画在了纸上,便形成了后世经典的奇异吸引子。从这张图中可以看出混沌与分形之间的联系,分形是混沌的几何表达。通过研究,洛伦茨终于明白了,长期的天气预报是不可能准确的,于是他写了一篇论文《一只蝴蝶拍一下翅膀会不会在Taxas州引起龙卷风?》,这就是“蝴蝶效应”的由来。
洛伦茨发现了混沌现象,但为这种现象取名的却另有其人,1972年美国数学家约克与其弟子,来自于我国福建省的李天岩发表了论文《周期3意味着混沌(Chaos)》,从而让“Chaos”成为混沌现象的名字。这里的周期3正好与《老子》中的三生万物不谋而合,所以不得不佩服我国先贤的智慧。
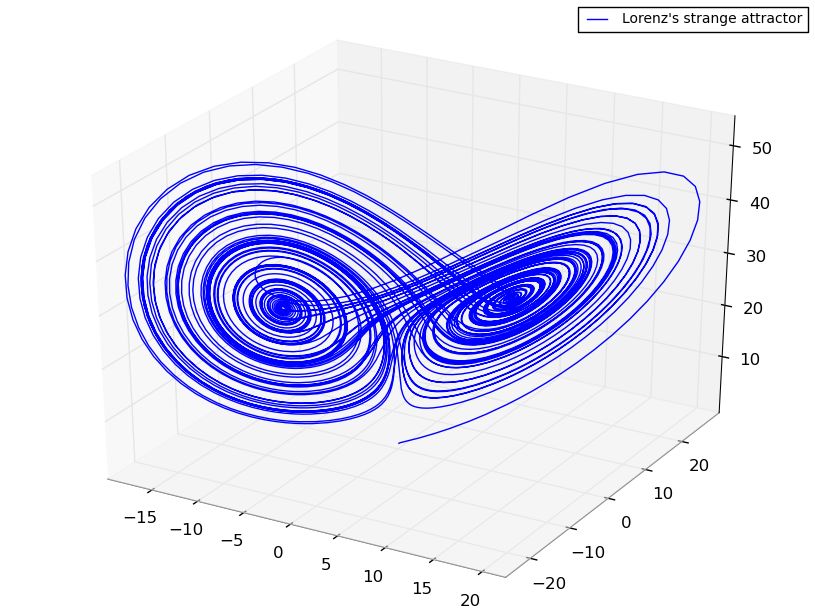
洛伦茨的奇异吸引子
如果说量子力学打破了微观世界的确定性,那么混沌则打破了人们对宏观世界确定性的认识,随着人们对混沌现象的不断深入研究,更进一步确信了,混沌才是我们所处世界的本质。例如在研究人的心率曲线时发现,健康成年人的心率曲线是不规则的形状,呈现某种自相似性,貌似混沌,而癫痫患者的心率曲线反而是呈现更多的规则性与周期性。混沌是人的生命之源,代表了生机。钱学森也有过“某一个层次上的混沌可以是高一个层次上的有序的推动力量”的论断。
混沌现象是非线性确定系统的本质属性,说明了世界是随机的,但随机中又孕育着有序。而系统的吸引子又将分形与混沌联系起来,分形是混沌的几何表达。因为混沌的不可预测性,从而产生了万千的复杂系统。
圣塔菲研究所与复杂性系统科学
分形和混沌是对非线性系统的数学表达。但现实世界中,我们所面临的系统较之混沌理论研究中描述的系统要复杂得多。人们对系统科学的目光最终都聚焦到了复杂性系统科学的研究上。1984年,受诺贝尔物理奖获得者,夸克之父盖尔曼提议,以来自洛斯阿拉莫斯国家实验室的科学家为主,共24位科学家在新墨西哥州建立了圣塔菲研究所,致力于复杂系统科学的研究。盖尔曼认为,“我们所要致力于研究的是跨越科学不同学科的大整合。有些领域如在分子生物学、非线性科学、认知科学等领域已经开始了,而这个新的研究所的任务就是要促使其诞生”。从此圣塔菲成为全世界复杂性系统科学研究者的圣地。
圣塔菲研究所认为:“复杂性产生于任何多个主体交互、相互适应以及主体适应环境的系统。这些交互和适应在宏观层面产生系统演化过程和常见的令人惊奇的涌现行为。复杂性科学试图找到能够在这样一些不同的物理、生物和社会等系统中导致这种复杂性的共同机理。”圣塔菲研究所陆续产生了一大批系统复杂性领域相关的科学家和知名的著作,其中影响最大的当属霍兰以及他提出的复杂适应系统理论。
复杂适应系统理论
霍兰是圣塔菲研究所的常驻科学家之一,他在研究了城市、蚁群、生态、胚胎、神经网络、人体免疫系统等复杂系统的基础上,拨开重重迷雾,提炼出了众多复杂系统演化过程中的一般性因素,即系统内部众多独立的要素的相互作用,使复杂系统作为一个整体产生了自发性的自组织,成为一种能够自主应对外界变化的自适应主体(Self-adaptive Agent)。1994年他提出了复杂适应系统理论(Complex Adaptive Systems,简称CAS)。复杂适应系统理论将系统当作自适应主体,具有通用的4种特性和3种机制。构成了复杂系统内部的“隐秩序”,成为推动复杂系统演化的动力。四种特性包括:
1)聚集。聚集有两种含义,一是指简化复杂系统的一种方法,我们常把相似的事物聚集成类,就好比面向对象方法中的类的抽象过程;二是指复杂系统组成的过程,各个底层模块分层次不断聚集,从而最终形成复杂系统本身。
2)非线性;复杂系统的聚集过程不是相同个体的数量累积,而是有复杂的交互过程,因此复杂系统必须是非线性的,非线性导致了混沌。
3)流;流是指系统内部信息、能量的流动,流是系统演化的动力之源。
4)多样性;多样性是复杂系统不断适应外界变化带来的必然结果。
三种机制包括:
1)标识;标识是聚集过程中为区分不同中间实体而被赋予的特征。
2)内部模型(机制);内部模型是指复杂系统内部的关联关系与模型机制,知晓了内部模型,我们才能对复杂系统行为进行建模和预测。
3)积木;积木是指系统的构成元素,积木是分层次和颗粒度的。
霍兰
自适应主体的适应性,是指它能够与环境以及其它主体进行交互作用。主体在这种持续不断的交互作用的过程中,不断地“学习”或“积累经验”,并且根据学到的经验改变自身的结构和行为方式,推动整个宏观系统的演变或进化,包括新层次的产生,分化和多样性的出现,新的、聚合而成的、更大的主体的出现等等。所以霍兰在其著作《隐秩序》中提出了“适应性造就复杂性”的论断。
模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,霍兰提出了遗传算法,实现了计算机模拟的自进化过程。霍兰又被称为遗传算法之父。遗传算法揭示了时间尺度上系统代系之间的演化规律,而复杂适应系统理论揭示了规模尺度上复杂系统的演化规律。
大自然的适应性进化
我们就以上篇提到的非洲大量出现不长牙的大象为例,来介绍复杂适应系统理论在大自然进化中的作用机制。
通常情况下非洲大象公象和母象都长象牙,象牙除了在生活上辅助觅食外,还肩负着打斗中保护自身的作用,因此长有象牙的大象的生存能力较强,自然选择下,长有象牙的大象数量比较多,仅存在少量因变异而未长象牙的大象,等同于象群中的残疾象。然而最近人们发现,在非洲的莫桑比克,出现了没有象牙的母象占多数的情况。因为长年战乱,军人屠杀长有象牙的母象,反而使因变异不长象牙的母象更能生存下来,久而久之改变了大象种群的基因,没有象牙的非洲母象又把这个基因传给了下一代,它们生出的孩子大部分又是没有象牙的非洲母象,这样母象没牙的基因,就这么一代代传了下来,最终,没牙的母象,从少数变成了多数。这就是象群系统为适应人类的行为而做出的适应性改变。地球是我们人类和动物共同生存的家园,我们应该站在人与自然共同组成的复杂适应系统的角度来重新审视自身的行为,做到和谐共处。
总结
分形与混沌一方面从几何和代数的角度对非线性系统的演化进行了描述,为开展复杂系统研究提供了数学基础;另一方面分形与混沌代表了自然界的普遍规律,为人们认识自然提供了全新的、客观的视角。复杂适应系统理论在规模尺度上揭示了复杂系统适应外部变化,不断演化的动力机制。而遗传算法则从时间尺度上揭示了复杂系统代系演化过程中的动力机制。非线性与复杂性更加接近了系统的本质,并将系统科学推进到了复杂性系统科学的新的高度。
人们研究系统科学,除了更好地认识我们所处的客观世界之外,更重要的是用于指导如何改造世界。制造和使用工具是人类进化过程中的重要里程碑。人们也通过使用工具来来改造自然,形成一系列技术。人类在使用技术,大规模地改造自然的过程形成了工程的概念,而为了更好地管理工程过程,人们总结经验发展出了系统工程方法,而工具的制作和工程的实施又需要有科学作为依据和指导。那么科学、技术、工程之间的关系到底怎样,人们又如何从系统科学研究过渡到系统工程研究,我们后续继续开展分析。
-
神经网络
+关注
关注
42文章
4789浏览量
101528 -
几何
+关注
关注
0文章
37浏览量
12408 -
人工智能
+关注
关注
1799文章
48047浏览量
241944
原文标题:系统科学发展之非线性与复杂适应系统理论
文章出处:【微信号:AItists,微信公众号:人工智能学家】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
“模电”基于ICT整合教学模式理论与实践探索课题研究实施方案
非线性控制系统的全局可镇定
非线性系统的模糊自适应输出反馈控制
无标度网络及其系统科学意义
时变非线性系统的自适应逆控制仿真
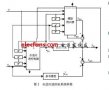
何长安非线性系统控制理论的PDF电子书免费下载
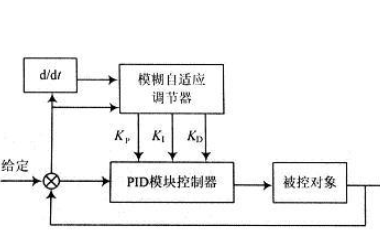




 系统科学发展之非线性与复杂适应系统理论
系统科学发展之非线性与复杂适应系统理论
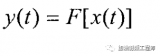











评论