噪声是干扰和妨碍人类认知和理解信息的重要因素,而图像噪声则是图像中干扰和妨碍人类认识和理解图像信息的重要因素。由于噪声本身具有不可预测性,可以将它当做一种随机误差(这种误差只有通过概率统计的方法来识别)。因此,图像噪声可以视为一种多维随机过程,可以选择随机过程的概率分布函数和概率密度函数来作为对图像噪声进行描述的方法。
1、图像噪声的分类
图像在采集和传输的过程当中必然会受到各种噪声在不同程度上的污染。根据图像和噪声之间的相互关系将噪声划分为以下三种形式:
(1)加性噪声
噪声和原始图像不相关,可以表示为:
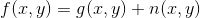
其中 f ( x , y ) 代表被污染的图像(噪声图像),g ( x , y ) 代表原始图像,n ( x , y ) 代表噪声。图像中的加性噪声一般是在图像的传输过程中由“信道噪声”和CCD摄像机对图像数字化的过程中产生的。
(2)乘性噪声
噪声和原始图像相关,可以表示为:
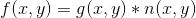
图像中的乘性噪声一般是由胶片中的颗粒、飞点扫描图像中的噪声、电视扫描光栅等原因造成的。
(3)量化噪声
图像中的量化噪声是图像在量化过程中图像从模拟到数字所产生的差异,是图像量化过程中的误差。
2、图像噪声的模型
图像中的噪声根据其概率分布的情况可以分为高斯噪声(Gaussian noise)、脉冲噪声(Impulsive noise)、瑞利噪声(Rayleigh noise)、伽马噪声(Gamma noise)、指数噪声(Exponential noise)和均匀噪声(Uniform noise)等各种形式。
(1)高斯噪声
高斯噪声是所有噪声当作使用最为广泛的,传感器在低照明度或者高温的条件下产生的噪声就属于高斯噪声,电子电路中产生的噪声也属于高斯噪声,还有很多噪声都可以根据高斯分布(正态分布)的形式进行描述。高斯噪声的概率密度函数可以表示为:
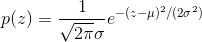
其中灰度值用z表示,灰度值的期望值用μ表示,灰度值的标准差用σ表示。高斯噪声的概率密度函数如下图所示:
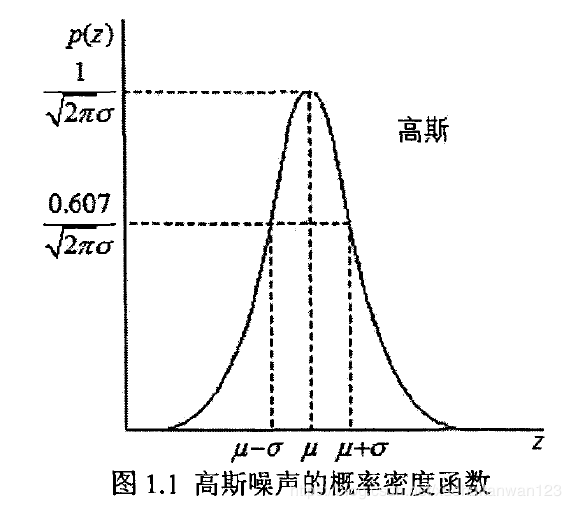
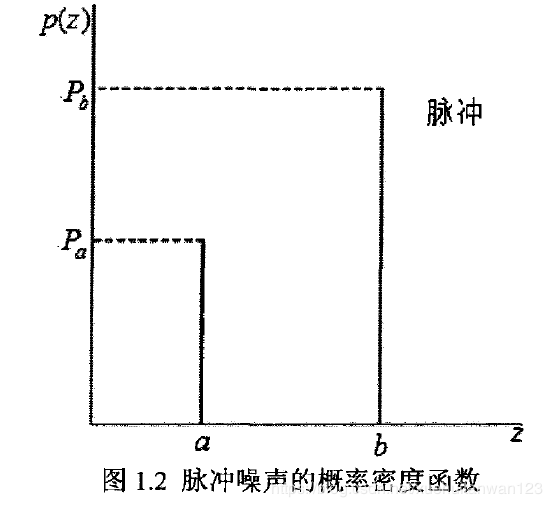
(2)脉冲噪声
脉冲噪声的概率密度函数可以表示为:
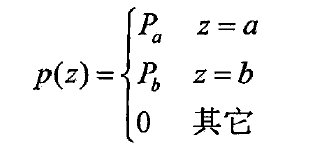
当a
脉冲噪声的概率密度函数分布图:
(3)瑞利噪声
瑞利噪声的概率密度函数可以表示为:
概率密度的均值为:
概率密度的方差为:
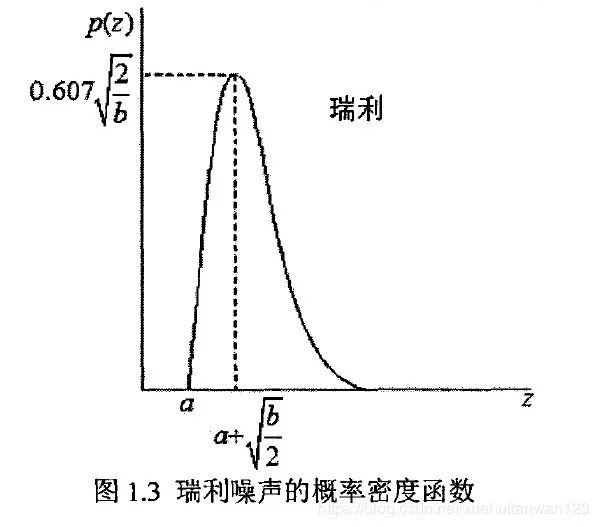
瑞利噪声的概率密度函数分布为:
(4)伽马噪声
伽马噪声的概率密度函数可以表示为:
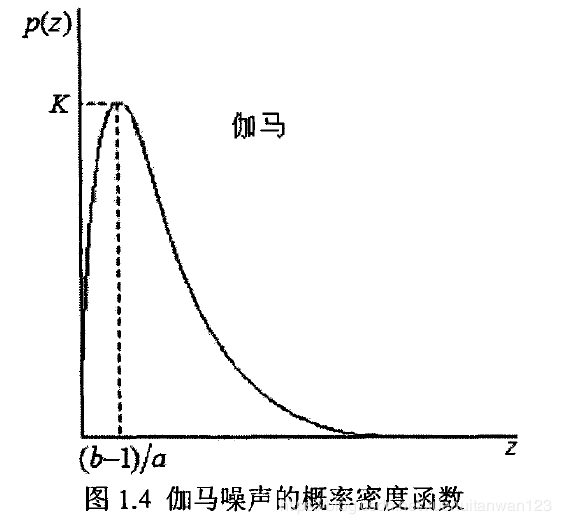
其概率密度函数分布图为:
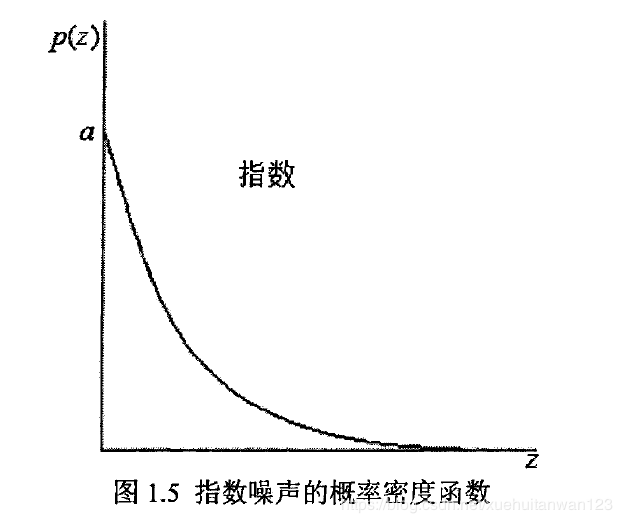
(5)指数函数
指数噪声的概率密度函数可以表示为:
其中 a>0。
概率密度的均值为:
概率密度的方差为:
其概率密度函数分布图为:
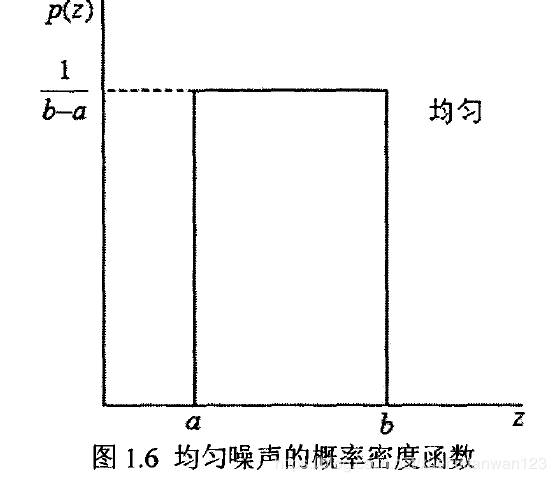
(6)均匀噪声
均匀噪声的概率密度函数可以表示为:
概率密度的均值为:
概率密度的方差为:
其概率密度函数分布为:
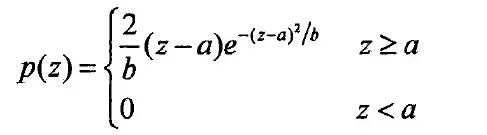
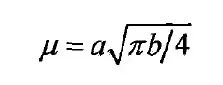
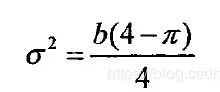
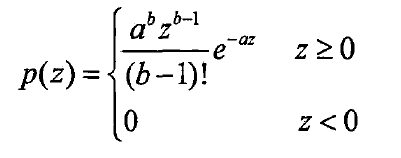

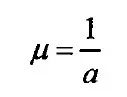
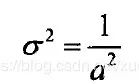
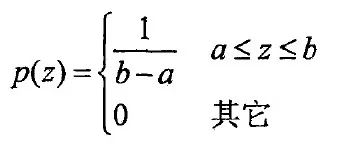
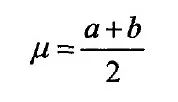
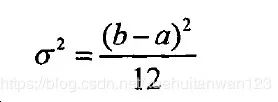
-
噪声
+关注
关注
13文章
1122浏览量
47436 -
图像
+关注
关注
2文章
1086浏览量
40492 -
函数
+关注
关注
3文章
4333浏览量
62707
原文标题:图像噪声的分类与模型
文章出处:【微信号:Imgtec,微信公众号:Imagination Tech】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
图像噪声基本知识的介绍和应用
图像中的高斯和脉冲混合噪声处理
基于乘性噪声的图像人工退化研究
CMOS图像传感器噪声抑制与多分辨率量化研究
数字图像高密度脉冲噪声的滤波算法

非局部平均方法对椒盐噪声图像滤波算法

基于图像局部灰度差异的噪声图像分割模型
数字图像噪声的四种分类方式
如何使用One-class SVM进行噪声图像分割方法的详细资料说明




 图像噪声的分类!图像噪声的模型
图像噪声的分类!图像噪声的模型












评论