深入卷积神经网络背后的数学原理

在计算机神经视觉技术的发展过程中，卷积神经网络成为了其中的重要组成部分，本文对卷积神经网络的数学原理进行了介绍。

文章包括四个主要内容：卷积、卷积层、池化层以及卷积神经网络中的反向传播原理。在卷积部分的介绍中，作者介绍了卷积的定义、有效卷积和相同卷积、跨步卷积、3D卷积。

在卷积层部分，作者阐述了连接切割和参数共享对降低网络参数学习量的作用。在池化层部分，作者介绍了池化的含义以及掩膜的使用。

自动驾驶、智能医疗、智能零售，这些曾被认为不可能实现的事情，在计算机视觉技术的帮助下，终于在最近成为了现实。今天，自动驾驶和自动杂货店的梦想不再像以前那样遥不可及。

事实上，每天我们都在使用计算机视觉技术帮助我们用人脸解锁手机，或者对即将发布到社交媒体上的照片进行自动修饰。

在计算机视觉技术应用这一巨大成功的背后，卷积神经网络（CNN）可能是其中最重要的组成部分。

在本文中，我们将逐步理解，神经网络是如何与 CNN 特有的思想协作的。本文章包含了相当复杂的数学方程式，但如果您对线性代数和微积分不熟悉，请不要气馁。

我的目标不是让您记住那些公式，而是让您从直觉上去理解这些公式背后隐藏的意义。

01

前言

在之前的系列中，我们学习了密集连接的神经网络（densely connected neural networks）。

这些网络的神经元被分成组，形成连续的层，相邻的两个层之间的神经元相互连接。下图展示了一个密集连接的神经网络的示例。

Figure 1.Densely connected neural network architecture

当我们解决分类问题时，如果我们的特征是一组有限的并有明确定义的特征，这种方法是很有效的——例如，根据足球运动员在比赛期间所记录的统计数据，预测该运动员的位置。

但是，当使用照片来进行预测时，情况会变得更加复杂。我们当然可以将每个像素的亮度视为一个单独的特征，并将其作为输入传递给我们的密集网络（dense network）。

不幸的是，为了使神经网络能够处理典型的智能手机照片，该网络必须包含数千万甚至数亿个神经元。

我们也可以通过缩小照片的尺寸来进行处理手机照片，但是这样做会使我们丢失很多有价值的信息。

可以发现，这种传统策略的性能很差，因此我们需要一种新的、更加聪明的方法来尽可能多地使用数据，并同时减少必要的计算和参数的数量。CNN 闪亮登场的时候到了。

02

数字图像的数据结构

首先花一点时间来解释一下数字图像的存储方式。数字图像实际上是巨大的数字矩阵。矩阵中的每个数字对应于其像素的亮度。

在 RGB 模型中，彩色图像由三个矩阵组成，分别对应三个颜色通道——红，绿，蓝。而在黑白图像中，我们只需要一个矩阵。

矩阵中的每个数字的取值区间都是 0 到 255。该范围是存储图像信息的效率（256个值刚好适合1个字节）与人眼的灵敏度（我们区分同种颜色的灰度级别的数量极限）之间的折衷。

Figure 2.Data structure behind digitalimages

03

卷积

核卷积（kernel convolution）不仅仅用于 CNN，它还是许多其他计算机视觉算法的关键要素。

核卷积就是将一个小数字矩阵（滤波器，也称作 kernel 或 filter）在图像上进行滑动，并根据 kernel 的值，对图像矩阵的值进行转换的过程。对图像经过卷积操作后得到的输出称为特征映射（feature map）。

特征映射的值的计算公式如下，其中 f 代表输入图像，h 代表滤波器 。结果矩阵的行数和列数分别用 m 和 n 表示。

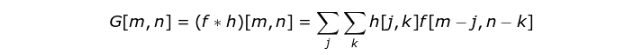
Figure 3.Kernel convolution example

将 kernel 放在选定的像素上后，我们从 kernel 中依次取出每个值，并将它们成对地与图像中的相应值相乘。

最后，我们将每个核运算后的结果元素相加，并将求和结果放在输出特征图中的正确位置上。

上图从微观角度详细地展示了这一运算的过程，但在完整图像上实施该运算的结果可能更加有趣。图4展示了使用几个不同 kernel 的卷积结果。

Figure 4.Finding edges with kernel convolution

04

有效卷积&相同卷积（Valid and Same Convolution）

正如我们在图3中看到的，当我们使用 3x3 的 kernel 对 6x6 图像执行卷积时，我们得到 4x4 的特征映射。

这是因为在这个图像中，只有16个位置可以将 kerenl 完整地放在这张图像中。由于每次执行卷积时我们的图像都会缩小，因此在我们的图像完全消失之前，我们只能进行有限次数的卷积。

另外，如果对 kernel 在图像中移动的过程进行观察，我们就会发现图像外围像素的影响远小于图像中心像素的影响。

这样会导致我们失去图像中包含的一些信息。下图展示了像素位置的改变对特征图的影响。

Figure 5.Impact of pixelposition

为了解决这两个问题，我们可以使用额外的边框来填充图像（padding）。例如，如果使用 1像素进行填充，我们将图像的大小增加到 8x8，因此使用 3x3 的 kernel 的卷积，其输出尺寸将为 6x6 。

在实践中，我们通常用零值来填充额外的边界。根据是否使用填充，我们将处理两种类型的卷积—— Valid 和 Same。

Valid —— 使用原始图像，Same —— 使用原始图像并使用它周围的边框，以便使输入和输出的图像大小相同。

在第二种情况下，填充宽度应满足以下等式，其中 p 是填充尺寸，f 是 kernel 尺寸（通常是奇数）。

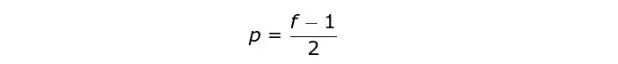
05

跨步卷积（Strided Convolution）

Figure 6.Example of strided convolution

在前面的例子中，我们总是每次将 kernel 移动一个像素，即步长为1。步长也可以视为卷积层的超参数之一。

图 6 展示了使用更大步长时的卷积运算。在设计 CNN 架构时，如果希望感知域重叠较少，或者希望让特征图的空间维度更小，我们可以增加步长。

输出矩阵的尺寸（考虑填充和步长时）可以使用以下公式计算。

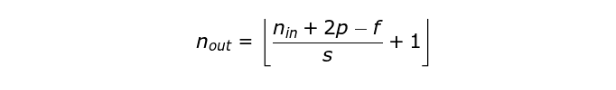
06

过渡到第三个维度

体积卷积（Convolution over volume）是一个非常重要的概念，这不仅使我们能够处理彩色图像，而且更为重要的是，我们能够在单层网络中使用多个 kernel 。

第一个规则是 kernel 和图像必须具有相同数量的通道。一般而言，图像的处理过程和图3的示例非常相似，但是这次我们是将三维空间中的值对相乘。

如果想在同一个图像上使用多个 kernel，首先我们要分别对每个 kernel 执行卷积，然后将结果从顶层向下进行叠加，最后将它们组合成一个整体。

输出张量的尺寸（可以称为3D矩阵）满足以下等式，其中：n - 图像大小，f  - 滤波器大小，nc  - 图像中的通道数，p - 填充大小，s -  步幅大小，nf  - kernel 的数量。

Figure 7.Convolution overvolume

07

卷积层

接下来我们将用前面学到的知识来构建 CNN 的一个层。我们将要用到的方法几乎与构建密集神经网络时用到的相同，唯一有区别的地方是，我们不再使用简单的矩阵乘法，而是使用卷积。

前向传播包括两个步骤。第一步是计算中间值 Z：首先将前一层的输入数据与张量 W（包含滤波器）进行卷积，然后将运算后的结果加上偏差 b 。

第二步是将中间值 Z 输入到非线性激活函数中（使用 g 表示该激活函数）。下面展示了矩阵形式的数学公式。

如果您对公式中的任何部分不太清楚，我强烈推荐您去阅读一下我之前的文章，文中详细讨论了密集连接的神经网络的具体内容。

下文的插图很好地展示了公式中各张量的维数，以助于理解。

Figure 8.Tensors dimensions

连接切割和参数共享（Connections Cutting and Parameters Sharing）

在本文的开头曾提到，由于需要学习大量的参数，密集连接的神经网络在处理图像方面的能力很差，而卷积却为该问题提供了一种解决方案，下面我们一起来看看卷积是如何优化图像处理的计算的。

在下图中，我们用一种略微不同的方式对 2D 卷积进行了可视化——用数字 1-9 标记的神经元构成输入层，用于接收输入图像的像素亮度，单元 A-D 表示经过卷积计算后得到的特征映射。

最后，I-IV 表示来自 kernel 的后续值，这些值是需要网络进行学习的。

Figure 9.Connections cutting and parameters sharing

现在，让我们关注卷积层的两个非常重要的属性。第一，从图中可以看到，并非两个相邻层中的所有神经元都相互连接。

例如，神经元 1 仅影响 A 的值。第二，我们可以发现一些神经元使用了相同的权重。这两个属性意味着在 CNN 中我们需要学习的参数要少得多。

值得一提的是，kernel 中的任一单值都会影响输出特征映射的每一个元素——这在反向传播的过程中是至关重要的。

08

卷积层的反向传播（Convolutional Layer Backpropagation）

任何曾经试图从头开始编写神经网络的人都知道，前向传播还不到最终成功的一半。当你开始向回推算时，真正的乐趣才刚刚开始。

如今，我们不需要为反向传播而烦恼——因为深度学习框架已经为我们做好了，但是我觉得有必要弄明白它背后发生的事情。

就像在密集连接的神经网络中一样，我们的目标是计算导数，然后在梯度下降的过程中，用这些导数去更新我们的参数值。

在下面的计算中，我们将用到链式法则 —— 这在我之前的文章中提到过。我们想要评估参数的变化对结果特征映射的影响，以及随之对最终结果的影响。

在开始详细讨论之前，我们需要将数学符号统一 —— 为了表示方便，我不会使用偏导数的完整符号，而是用下面提到的缩符号。

但是请记住，当我使用这种表示法时，这将始终代表着成本函数的偏导。

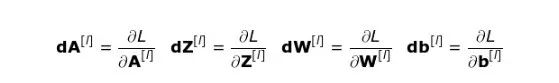
Figure 10.Input and output data for a single convolution layer in forward and backward propagation

我们的任务是计算 dW [1] 和 db [l] （它们是与当前层参数相关的导数），以及 dA[l-1]（它将被传递给前一层）。

如图10所示，dA[l] 作为输入，张量 dW 和 W，db 和 b 以及 dA 和 A 的维度分别相同。第一步是求激活函数关于输入张量的导数，将其结果记为 dZ [1] 。根据链式法则，该运算的结果将在后面用到。

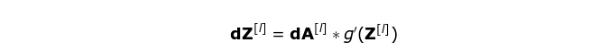
现在，我们需要处理卷积自身的反向传播。为了实现这个目标，我们将利用一个称为全卷积的矩阵运算，该运算的可视化解释如下图所示。

请注意，在此过程中我们要使用 kernel，而我们之前用到的 kernel 是该 kernel 旋转了180度所得到的。

该操作可以用以下公式表示，其中 kernel 由 W 表示，dZ[m,n] 是一个标量，该标量属于从前一层所获得的偏导数。

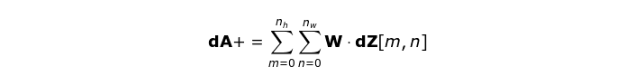
Figure 11.Full convolution

09

池化层（Pooling Layers）

除了卷积层之外，CNN 经常使用一个称为池化层的网络层，它们主要用于减小张量的大小并加快计算速度。

这个层的结构很简单，我们只需要将图像划分成不同的区域，然后对每个部分执行一些操作即可。

例如，对于最大池化层（Max Pool Layer），我们从每个区域中选择一个最大值，并将其放在输出中的相应位置即可。

与卷积层的情况一样，我们有两个超参数——kernel 的尺寸和步长。

最后值得一提是，如果要为多通道图像执行池化操作，则每个通道都应该分别执行池化操作。

Figure 12.Max poolingexample

10

池化层的反向传播（Pooling Layers Backpropagation）

在本文中，我们仅讨论最大池化的反向传播（max pooling backpropagation），但是通过将该方法稍作调整，便可运用到其他所有类型的池化层。

由于在池化层这种类型的层中，我们不用更新任何参数，我们的任务只是适度地分配梯度值。

前文讲到，在最大池化的前向传播中，我们从每个区域中选择最大值并将它们传输到下一层。

因此很明显，在反向传播期间，梯度不会影响未在前向传播中使用的矩阵元素。

在实际操作中，该过程是通过创建一个掩膜（mask）来实现的，该掩膜会记住在前向传播中所使用的元素的位置，随后我们就可以用该掩膜来传递梯度。

Figure 13.Max pooling backwardpass