蒙特卡罗树搜索(MCTS)算法执行基于模拟的搜索以改进在线策略。在搜索过程中,模拟策略适用于探索最有希望的游戏策略。MCTS已被用于处理许多最新的程序问题,但MCTS的一个缺点是需要评估状态值并存储其结果,这在分支树非常多的游戏场景中并不适用。
作者提出了一种替代性的基于模拟的搜索方法,即策略梯度搜索(PGS),该方法通过策略梯度更新在线调整神经网络模拟策略,避免了对搜索树的需求。在Hex中,PGS实现了与MCTS相当的性能,并且使用专家迭代算法(Expert Iteration)和 PGS训练的模型击败了MoHex 2.0,这是目前最强的开源Hex代理。

蒙特卡罗树搜索(MCTS)在Go和Hex等游戏中实现最大测试时间性能的价值早已为人所知。最近的研究表明,在许多经典的棋盘类游戏中,通过专家迭代算法将规划方法纳入强化学习智能体的训练,可以使用纯RL方法实现最好的性能。
但是,MCTS构建一个显式搜索树,每个节点会存储其访问数和估计值。所以在MCTS中需要多次访问搜索树中的节点。这种方法适用许多经典的棋盘游戏,但在许多现实世界的问题中,分支树都会非常大,这使得MCTS难以使用。大量的分支树可能由非常大的动作空间或偶然节点引起。在动作空间很大时,可以使用先前策略来降低弱动作的影响,从而减少有效分支树。随机转换更难以处理,因为先前的策略不能用于减少偶然节点处的分支因子。
相比之下,蒙特卡罗搜索(MCS)算法没有这样的要求。MCTS使用每个节点中的值估计来调整模拟策略,而MCS算法在整个搜索过程中都有固定的模拟策略。但是,由于MCS在搜索过程中不能提高模拟质量,因此它的效果会明显弱于MCTS。
基础理论:
1)Markov Decision Processes(MDP):马尔可夫决策过程在每个时间间隔t中,代理观察状态并选择要采取的动作。对于终止状态,需要最大化阶段性奖励R。
2)Hex:Hex 是一个基于双人的基于连接的游戏,在n×n六边形网格上进行。游戏双方分别用黑色和白色棋子表示,双方轮流在空的位置上放置自己的棋子。如果白棋从左到右连续成线则白棋赢,若黑色棋子从上到下连成线则黑棋赢,下图是白棋赢的示意图。

3)Monte Carlo Tree Search(MCTS):蒙特卡罗树搜索是一种随时可用的最佳树搜索算法。它使用重复的游戏模拟来估计状态值,并使用更优的游戏策略进一步扩展搜索树。当所有分支都模拟完成后,采取reward值最高的action。
4)Monte Carlo Search(MCS):蒙特卡罗搜索是一种比MCTS更简单的搜索算法。给定状态和策略,通过迭代的模拟选择评估值最高的策略。
5)Expert Iteration:搜索算法基于单个状态s0的规划模型动作,但不学习推广到不同位置的信息。相比之下,深度神经网络能够在状态空间中推广知识。专家迭代算法将基于搜索的规划方法和深度学习进行了结合,其中规划算法作为专家,用于发现对当前策略的改进内容。神经网络算法作为学员,其模仿专家的策略并计算值函数。
Policy Gradient Search
策略梯度搜索通过应用无模型的强化学习算法来适应蒙特卡罗搜索中的模拟过程。作者假设提供先验策略π和先验值函数V,并在完整MDP上训练。
该算法必须对它通过非表格函数逼近器学习的所有内容进行表示,否则它将遇到与MCTS相同的问题。MCTS已经是一种自我对弈强化学习方法,但不能直接使其适应函数逼近,因为UCT公式依赖于基于访问量的探索规则。
作者使用策略梯度强化学习方法来训练模拟策略。模拟策略由具有与全局策略网络相同的体系结构的神经网络表示。在每个游戏开始时,策略网络的参数被设置为全局策略网络的参数。
由于评估模拟策略代价很大,所以该算法不会模拟到终止状态,而是使用截断的蒙特卡罗算法模拟。选择何时截断模拟并不简单,最佳选择策略可能取决于MDP本身。如果模拟太短,可能无法包含新的信息,或者没有给出足够长的时间范围搜索。太长的模拟则会导致恨到的时间开销。

对于Hex,作者使用与MCTS算法相同的策略:运行每个模拟过程,直到模拟的动作序列是唯一的。一旦我们在t步之后达到模拟的终止状态sL,使用全局值网络V估计该状态的值,并使用该估计更新模拟策略参数θ,其中α是学习率,其值在-1和1之间,对于其他问题,可能需要非零基线。可以将这些更新视为微调当前子游戏的全局策略。
因为在每次模拟中都要访问根节点,与 MCS 一样,可以使用基于单状态的强化学习方法来选择每个模拟的第一个动作。采用PUCT公式,选择令下式的值的动作:
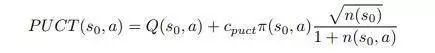
Parameter Freezing during Online Adaptation
在测试期间,在线搜索算法通常受在时间约束的情况下使用,因此,与标准RL问题相比,其使用数量级更少的模拟。还需要注意的是,要确保该算法在每个模拟步骤中不需要太多计算。当在专家迭代中用于离线训练时,搜索方法的效率仍然至关重要。
Note on Batch Normalisation
神经网络使用批量标准化。在所有情况下,全局神经网络已经在来自许多独立采样的Hex游戏的状态数据集上进行了训练。
实验
Policy Gradient Search as an Online Planner
作者在Hex游戏中评估PGS。Hex具有中等数量的分支因子和确定性转换,这意味着MCTS在该领域中非常有效,这使作者能够直接比较PGS与MCTS的强度。作者在原始神经网络和四个搜索算法MCS,MCTS,PGS和PGS-UF之间进行了循环对弈,其中参数可变。为了克服Hex中第一个玩家具有的优势,每对智能体互相打了2*n*n场比赛。
每个智能体在每次移动使用800次搜索迭代,不会在移动之间思考。实验结果见下表。

如果策略搜索的能力已经饱和,那么PGS的扩展可能不如MCTS,但是并没有发现在游戏中会出现这种情况。但是,在每次移动中进行1600次迭代仍然是一个相当短的搜索,这样的情况可能会发生在较长时间的搜索过程中。

Policy Gradient Search Expert Iteration
作者使用PGS作为专家迭代算法中的专家进行实验,并与MCS和MCTS进行比较。
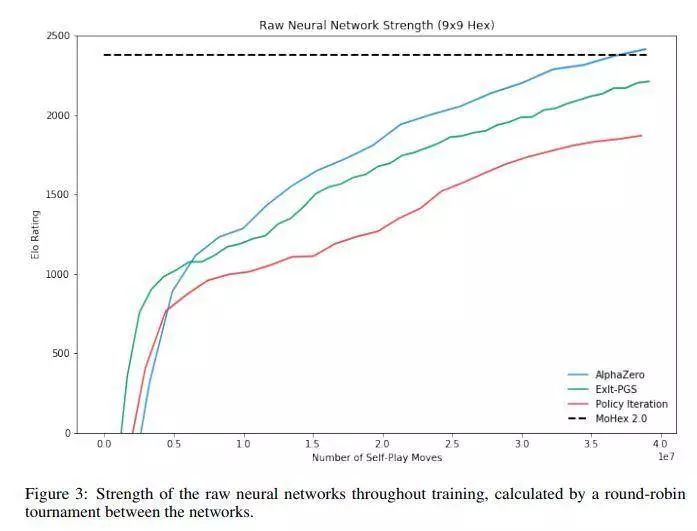
结果表明,PGS的性能优于MCS,但不如MCTS。在训练过程中,在反复应用更好或更差的专家时,智能体的差异更加复杂多变。
结论
作者提出了PGS算法,这是一种在线规划的搜索算法,不需要显式搜索树。PGS是一种有效的规划算法。实验结果证明,在9x9和13x13 的Hex游戏中,它的性能略微弱于MCTS,但与MCTS相比具有竞争力,同时其决策时间显著性能优于MCS。
在专家迭代算法的框架中使用PGS时,PGS在训练期间也很有效,该算法在不使用搜索树的情况下,训练了第一个有竞争力的Hex代理tabula rasa。相比之下,该算法比类似的强化学习算法和使用MCTS专家的专家迭代算法性能要好。
实验结果显示PGS-EXIT在专家迭代算法框架中性能明显优于MCS,并且还提供了第一个经验数据,表明MCTS-EXIT算法优于传统的策略迭代方法。
这项工作中提出的结果主要关注Hex的确定性和离散动作空间域。这使得模型的效果可以与MCTS直接比较,但PGS最激动人心的潜在应用是MCTS不易使用的问题,例如随机状态转换或连续动作空间的问题。
-
神经网络
+关注
关注
42文章
4771浏览量
100719 -
算法
+关注
关注
23文章
4607浏览量
92840 -
深度学习
+关注
关注
73文章
5500浏览量
121113
原文标题:策略梯度搜索:不使用搜索树的在线规划和专家迭代 | 技术头条
文章出处:【微信号:rgznai100,微信公众号:rgznai100】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
渐进式神经网络结构搜索技术
一种改进的快速搜索算法
一种新型全搜索运动估计IP核设计
一种结合梯度下降法的二层搜索粒子群算法
一种解决连续问题的真实在线自然梯度行动者-评论家算法
基于增强描述的代码搜索方法
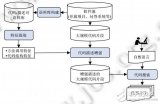
基于语义聚类的资源搜索策略
一种路径过滤性搜索算法
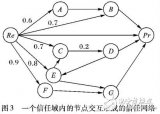
一种利用强化学习来设计mobile CNN模型的自动神经结构搜索方法
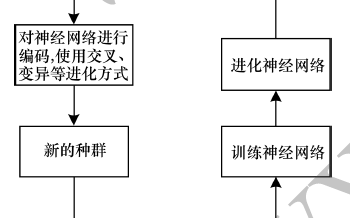
以进化算法为搜索策略实现神经架构搜索的方法
一种基于用户偏好的权重搜索及告警选择方法





 一种替代性的基于模拟的搜索方法,即策略梯度搜索
一种替代性的基于模拟的搜索方法,即策略梯度搜索











评论