四旋翼姿态控制通常选用 PID控制器作为主控环节,但 PID 控制器的参数不易整定,调控结果也存在较大的系统超调量,难以获得满意的控制效果。因此设计了 PI-PD 控制器的四旋翼姿态控制方式,其中 PI 控制器能够使系统快速无稳态误差的收敛,PD 控制器可以有效的抑制系统超调量。仿真结果表明:PI-PD 控制器能够很好的抑制系统超调量,缩短系统收敛时间,具有良好的控制效果。
近年来,随着微型系统、微型传感器、惯导技术以及飞行控制等技术的发展,四旋翼飞行器(以下简称四旋翼)引起了人们的广泛关注。四旋翼是通过改变四个旋翼的转速来调整其在空中的飞行姿态,包括俯仰角 θ、横滚角 φ、偏航角 ψ,从而控制机体水平方向上的运动,因此四旋翼的姿态控制是决定其飞行性能的关键所在。在工业过程控制和航空航天控制等领域中,PID 控制的应用达到 80 % 以上,不过由于四旋翼系统的强非线性、惯性和延迟,PID 控制器对四旋翼姿态的调整效果往往出现较多的系统超调量,或者调整时间较长,控制
效果并不令人满意。因此,设计一种能够抑制系统超调量,并且保证系统快速收敛的控制器,
可以提高四旋翼系统的稳定性和控制性。
1 PID控制器基本原理
PID 控制器结构简单、方便调试,广泛应用于工业生产中。PID 控制器是根据系统输出的误差值调节系统输出的控制形式,包含比例控制(P)、积分控制(I)和微分控制(D),其连续 PID 控制的结构形式为:
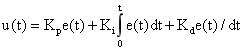
(1)
其中 u(t) 为系统输出,Kp、Ki、Kd 分别为比例、积分和微分系数,e(t)=y(r)-y(t) 为期望值与输出量的差值,即输出误差。而对于数字控制系统,可将 PID 控制器离散化,得到离散 PID 的结构形式:
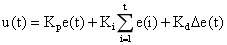 (2)
(2)
其中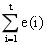 , 为所有误差值累加之和,Δe(t)=e(t)-e(t-1),等效微分运算。当期望值在相邻的采样周期保持不变时,y(r)=y(r-1),Δe(t)=-y(t)+y(t-1),Δe(t) 即为系统输出的变化量。
, 为所有误差值累加之和,Δe(t)=e(t)-e(t-1),等效微分运算。当期望值在相邻的采样周期保持不变时,y(r)=y(r-1),Δe(t)=-y(t)+y(t-1),Δe(t) 即为系统输出的变化量。
若基于 PID 控制器来对四旋翼的姿态进行调控,参数整定难度较大,调控效果不佳。鉴于此,本文基于文章 [6] 提出的 PI-PD 控制器,设计了基于 PI-PD 控制器的四旋翼姿态控制方式,用于减小系统超调量,缩短系统收敛时间,提高四旋翼在空中飞行的稳定性和控制性。
2 PI-PD控制器
PID 控制器对于高阶时滞系统、复杂的模糊系统以及不确定系统而言,控制效果不佳。而在 PID 控制器基础上演变而来的 PI-PD 控制器,对于含有积分、振荡或不稳定环节的控制对象,可以实现较好的闭环控制。PI-PD 控制器其结构图如图 1 所示。
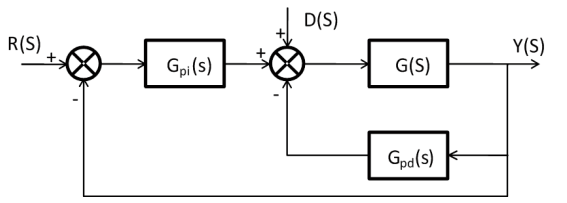
图 2:PI-PD 控制器等效结构图
设 PI 控制器和 PD 控制器的传递函数为:
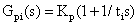 (3)
(3)
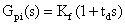 (4)
(4)
其中 Kp、Ti 分别 PI 控制器的比例和积分系数,Kf、Td 分别为 PD 控制器的比例和微分系数。图中,PI 控制器仍处于主控环节上,根据期望值调节输出量,具有决定系统收敛快慢和消除稳态误差的作用。而 PD 控制器成为了反馈环节,具有抑制系统振荡和超调量的作用,并且只与系统输出变化量有关,与期望值无关。

图 2:PI-PD 控制器等效结构图
为了简化 PI-PD 控制器结构,将其进行结构变换,得到图 2 所示的等效结构图。可得到主控环节 PI+PD 控制器为:
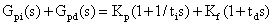 (5)
(5)
设 PID 控制器传递函数为:
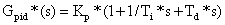 (6)
(6)
其中 Kp*、Ti*、Td* 分别为 PID 控制器的参数。于是可将式(5)整理成式(6)的类似形式:
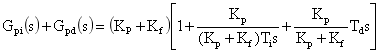
(7)
设 Kp=βKf,参数 β 表示 Kp 与 Kf 的关系,式(7)可变换为:
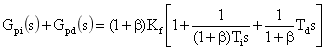
(8)
比较式(6)与式(8),可得出 Kp*、Ti*、Td* 与 Kp、Ti、Kf、Td 之间的关系表达式:
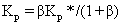 (9)
(9)
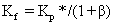 (10)
(10)
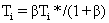 (11)
(11)
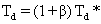 (12)
(12)
根据式(9)和(11)可得:
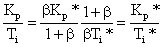 (13)
(13)
根据式(10)和(12)可得:
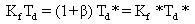 (14)
(14)
由此可以看出,根据 PID 控制器的 Kp*参数以及 β 值可以计算出 PI-PD 控制器的 Kp和 Kf 参数,β 决定了 Kp 与 Kf 的分配比例。式(13)和(14)表明,PI-PD 控制器的积分
控制和微分控制与 PID 控制器的参数相同。因此 PI-PD 控制器可以根据 PID 控制参数和 β 值计算得出 Kp、Ti、Kf、Td 参数,通过参数再次整定,能使系统在超调量较小、收敛时间较短的情况下平稳收敛,具有良好的调控效果。
3 仿真分析
通过 Adams 软件建立四旋翼动力学虚拟样机,将 Adams 所建模型与 Matlab/Simulink进行联合仿真,研究控制器对四旋翼姿态控制的调节效果。本文研究的四旋翼参数为:机体质量 m=0.67kg,对称电机轴距 l=450mm,旋翼转速与升力关系 8000r/m=9.8N,角度初始值俯仰角 θ=0°、俯仰角期望值 y(r)=0°,仿真步长 t=0.01s。横滚角 φ 与偏航角 ψ 的仿真结
果类同,本文不再赘述。
(1)使用 PID 控制器调节俯仰角 θ 的角度,整定一组参数 Kp=18、Ki=0.2、Kd=260。而根据 PID 控制器参数,设定不同的 β 值,计算出 PI-PD 控制器的 Kp、Ti、Kf、Td 的参数,仿真结果如图 3 所示。
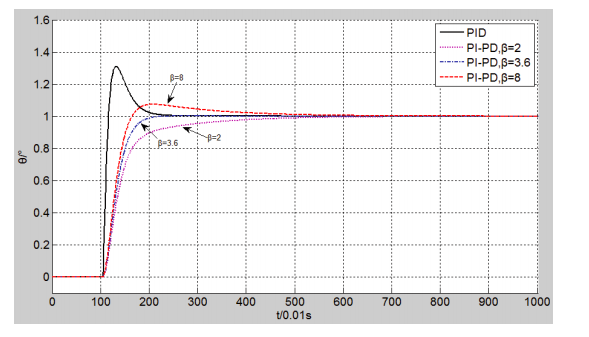
图 3:PI-PD 控制器不同 β 值仿真结果
在 1s 的时刻,期望值 y(r) 从 0°变为 1°,俯仰角 θ 在 PID 控制器的调节下,收敛时间约为 1.8s,系统超调量约为 30%。
与 PID 控制器的仿真结果比较,当 β 不同时,PI-PD 控制器具有不同的调节效果。而当 β=3.6 时,系统超调量极小,且收敛时间与PID 控制器基本相同。由此可以证明,选取合适的 β 值,PI-PD 控制器可以有效的抑制系统超调量,提高了系统的稳定性。
(2)为 了 使 系 统 收 敛 时 间 更 短, 根据 PI-PD 控制器的调节特性,重新整定参数Kp、Ki、Kd 和 β,仿真结果如图 4 所示。
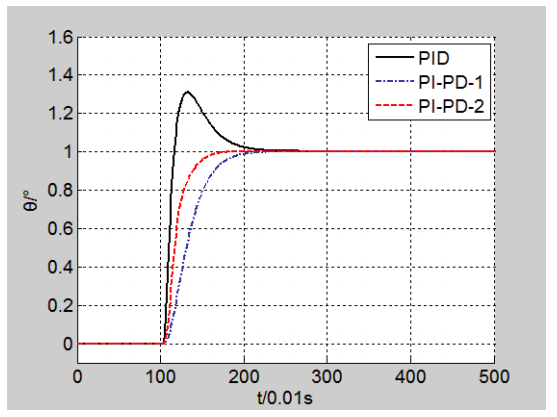
图 4:PI-PD 控制器不同整定参数仿真结果
仿真结果表明:PID 与 PI-PD-1 的收敛时间约为 1.8s,而 PI-PD-2 的收敛时间约为 0.8s,明显快于前两种控制效果。由此证明 PI-PD 控制器对于不同的整定参数,可以在系统无超调量的情况下,缩短系统收敛时间,提高了系统的控制性。
4 结束语
由于四旋翼的非线性和时滞特性,基于PID 控制器的四旋翼姿态控制方式的调节效果较难满足人们需求。本文基于 PI-PD 控制器,设计了新的四旋翼姿态控制方式。PI-PD 控制器方式可以利用已经整定好的 PID 控制器的参数,根据 β 值计算出控制参数。仿真结果表明
PI-PD 控制器能够使系统稳定收敛,且很好的抑制了系统超调量,获得了良好的控制效果。
在今后的工作中,将继续研究 PI-PD 控制器的参数整定、响应时间、鲁棒性等问题,获得更好的四旋翼姿态控制效果。
-
pcb
+关注
关注
4322文章
23128浏览量
398620 -
华强pcb线路板打样
+关注
关注
5文章
14629浏览量
43090
发布评论请先 登录
相关推荐
Diodes高性能USB PD3.1 EPR Sink控制器概述
SLD-ZX80阻旋料位控制器在工业领域的作用
ad怎么把原理图和pcb相关联
开源项目!用ESP8266 DIY会爬墙的无人机
PMP21254.1-具有集成 FET 控制器的 160A 四相 PCB layout 设计

高清画质、低时延,图传技术如何展现FPV穿越机的“速度与激情”

上海峰飞航空领先全球低空飞行器领域,展望2040年
基于非线性自适应学习控制器的四轴飞行器避障方案
四旋翼无人机飞行原理【其利天下无人机方案开发】

基于RT-Thread与滑模控制的微型多旋翼定点控制系统研究




 PI-PD 控制器的四旋翼飞行器PCB设计和原理图
PI-PD 控制器的四旋翼飞行器PCB设计和原理图











评论