用tensorflow,pytorch这类深度学习库来写一个神经网络早就不稀奇了。
可是,你知道怎么用python和numpy来优雅地搭一个神经网络嘛?
现如今,有多种深度学习框架可供选择,他们带有自动微分、基于图的优化计算和硬件加速等各种重要特性。对人们而言,似乎享受这些重要特性带来的便利已经是理所当然的事儿了。但其实,瞧一瞧隐藏在这些特性下的东西,能更好的帮助你理解这些网络究竟是如何工作的。
所以今天,文摘菌就来手把手教大家搭一个神经网络。原料就是简单的python和numpy代码!
符号说明
在计算反向传播时, 我们可以选择使用函数符号、变量符号去记录求导过程。它们分别对应了计算图中的边和节点来表示它们。
给定R^n→R和x∈R^n, 那么梯度是由偏导∂f/∂j(x)组成的n维行向量
如果f:R^n→R^m和x∈R^n,那么Jacobian矩阵是下列函数组成的一个m×n的矩阵。
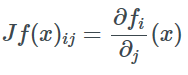
对于给定的函数f和向量a和b如果a=f(b)那么我们用∂a/∂b表示Jacobian矩阵,当a是实数时则表示梯度
链式法则
给定三个分属于不同向量空间的向量a∈A及c∈C和两个可微函数f:A→B及g:B→C使得f(a)=b和g(b)=c,我们能得到复合函数的Jacobian矩阵是函数f和g的jacobian矩阵的乘积:
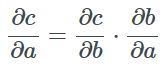
这就是大名鼎鼎的链式法则。提出于上世纪60、70年代的反向传播算法就是应用了链式法则来计算一个实函数相对于其不同参数的梯度的。
要知道我们的最终目标是通过沿着梯度的相反方向来逐步找到函数的最小值 (当然最好是全局最小值), 因为至少在局部来说, 这样做将使得函数值逐步下降。当我们有两个参数需要优化时, 整个过程如图所示:
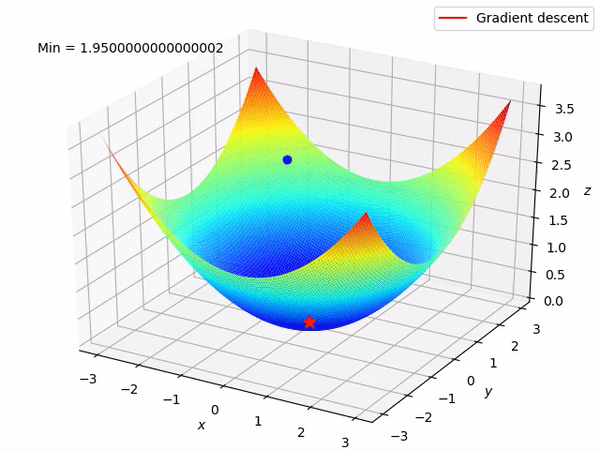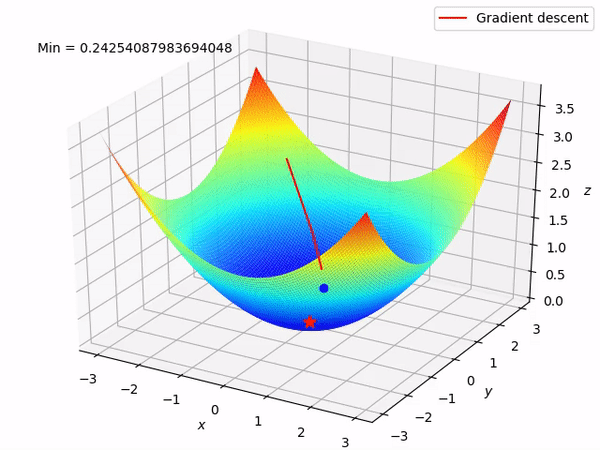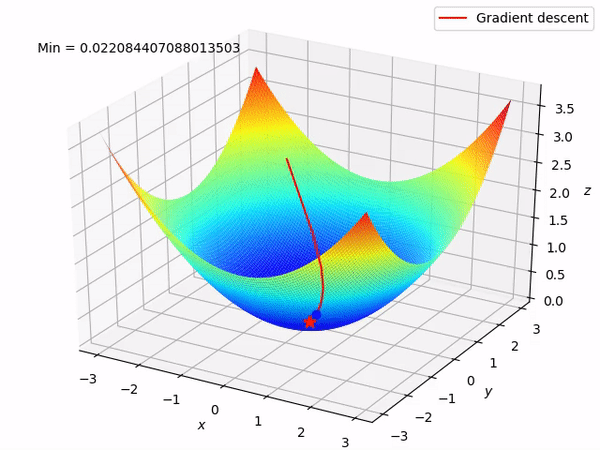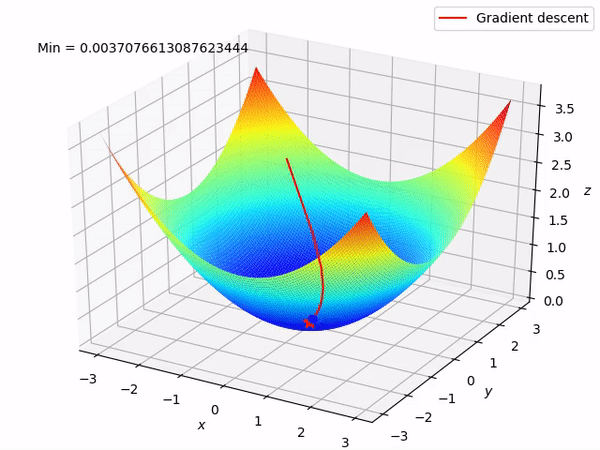
反向模式求导
假设函数fi(ai)=ai+1由多于两个函数复合而成,我们可以反复应用公式求导并得到:
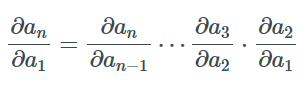
可以有很多种方式计算这个乘积,最常见的是从左向右或从右向左。
如果an是一个标量,那么在计算整个梯度的时候我们可以通过先计算∂an/∂an-1并逐步右乘所有的Jacobian矩阵∂ai/∂ai-1来得到。这个操作有时被称作VJP或向量-Jacobian乘积(Vector-Jacobian Product)。
又因为整个过程中我们是从计算∂an/∂an-1开始逐步计算∂an/∂an-2,∂an/∂an-3等梯度到最后,并保存中间值,所以这个过程被称为反向模式求导。最终,我们可以计算出an相对于所有其他变量的梯度。
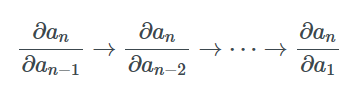
相对而言,前向模式的过程正相反。它从计算Jacobian矩阵如∂a2/∂a1开始,并左乘∂a3/∂a2来计算∂a3/∂a1。如果我们继续乘上∂ai/∂ai-1并保存中间值,最终我们可以得到所有变量相对于∂a2/∂a1的梯度。当∂a2/∂a1是标量时,所有乘积都是列向量,这被称为Jacobian向量乘积(或者JVP,Jacobian-Vector Product)。
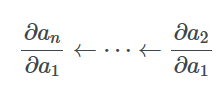
你大概已经猜到了,对于反向传播来说,我们更偏向应用反向模式——因为我们想要逐步得到损失函数对于每层参数的梯度。正向模式虽然也可以计算需要的梯度, 但因为重复计算太多而效率很低。
计算梯度的过程看起来像是有很多高维矩阵相乘, 但实际上,Jacobian矩阵常常是稀疏、块或者对角矩阵,又因为我们只关心将其右乘行向量的结果,所以就不需要耗费太多计算和存储资源。
在本文中, 我们的方法主要用于按顺序逐层搭建的神经网络, 但同样的方法也适用于计算梯度的其他算法或计算图。
深度神经网络
在典型的监督机器学习算法中, 我们通常用到一个很复杂函数,它的输入是存有标签样本数值特征的张量。此外,还有很多用于描述模型的权重张量。
损失函数是关于样本和权重的标量函数, 它是衡量模型输出与预期标签的差距的指标。我们的目标是找到最合适的权重让损失最小。在深度学习中, 损失函数被表示为一串易于求导的简单函数的复合。所有这些简单函数(除了最后一个函数),都是我们指的层, 而每一层通常有两组参数: 输入 (可以是上一层的输出) 和权重。
而最后一个函数代表了损失度量, 它也有两组参数: 模型输出y和真实标签y^。例如, 如果损失度量l为平方误差, 则∂l/∂y为 2 avg(y-y^)。损失度量的梯度将是应用反向模式求导的起始行向量。
Autograd
自动求导背后的思想已是相当成熟了。它可以在运行时或编译过程中完成,但如何实现会对性能产生巨大影响。我建议你能认真阅读 HIPS autograd的 Python 实现,来真正了解autograd。
核心想法其实始终未变。从我们在学校学习如何求导时, 就应该知道这一点了。如果我们能够追踪最终求出标量输出的计算, 并且我们知道如何对简单操作求导 (例如加法、乘法、幂、指数、对数等等), 我们就可以算出输出的梯度。
假设我们有一个线性的中间层f,由矩阵乘法表示(暂时不考虑偏置):
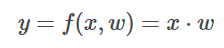
为了用梯度下降法调整w值,我们需要计算梯度∂l/∂w。这里我们可以观察到,改变y从而影响l是一个关键。
每一层都必须满足下面这个条件: 如果给出了损失函数相对于这一层输出的梯度, 就可以得到损失函数相对于这一层输入(即上一层的输出)的梯度。
现在应用两次链式法则得到损失函数相对于w的梯度:
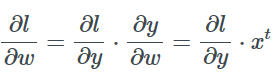
相对于x的是:
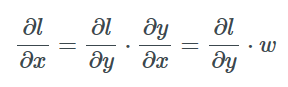
因此, 我们既可以后向传递一个梯度, 使上一层得到更新并更新层间权重, 以优化损失, 这就行啦!
动手实践
先来看看代码, 或者直接试试Colab Notebook
我们从封装了一个张量及其梯度的类(class)开始。
现在我们可以创建一个layer类,关键的想法是,在前向传播时,我们返回这一层的输出和可以接受输出梯度和输入梯度的函数,并在过程中更新权重梯度。
然后, 训练过程将有三个步骤, 计算前向传递, 然后后向传递, 最后更新权重。这里关键的一点是把更新权重放在最后, 因为权重可以在多个层中重用,我们更希望在需要的时候再更新它。
class Layer: def __init__(self): self.parameters = [] def forward(self, X): """ Override me! A simple no-op layer, it passes forward the inputs """ return X, lambda D: D def build_param(self, tensor): """ Creates a parameter from a tensor, and saves a reference for the update step """ param = Parameter(tensor) self.parameters.append(param) return param def update(self, optimizer): for param in self.parameters: optimizer.update(param)
标准的做法是将更新参数的工作交给优化器, 优化器在每一批(batch)后都会接收参数的实例。最简单和最广为人知的优化方法是mini-batch随机梯度下降。
class SGDOptimizer(): def __init__(self, lr=0.1): self.lr = lr def update(self, param): param.tensor -= self.lr * param.gradient param.gradient.fill(0)
在此框架下, 并使用前面计算的结果后, 线性层如下所示:
class Linear(Layer): def __init__(self, inputs, outputs): super().__init__() tensor = np.random.randn(inputs, outputs) * np.sqrt(1 / inputs) self.weights = self.build_param(tensor) self.bias = self.build_param(np.zeros(outputs)) def forward(self, X): def backward(D): self.weights.gradient += X.T @ D self.bias.gradient += D.sum(axis=0) return D @ self.weights.tensor.T return X @ self.weights.tensor + self.bias.tensor, backward
接下来看看另一个常用的层,激活层。它们属于点式(pointwise)非线性函数。点式函数的 Jacobian矩阵是对角矩阵, 这意味着当乘以梯度时, 它是逐点相乘的。
class ReLu(Layer): def forward(self, X): mask = X > 0 return X * mask, lambda D: D * mask
计算Sigmoid函数的梯度略微有一点难度,而它也是逐点计算的:
class Sigmoid(Layer): def forward(self, X): S = 1 / (1 + np.exp(-X)) def backward(D): return D * S * (1 - S) return S, backward
当我们按序构建很多层后,可以遍历它们并先后得到每一层的输出,我们可以把backward函数存在一个列表内,并在计算反向传播时使用,这样就可以直接得到相对于输入层的损失梯度。就是这么神奇:
class Sequential(Layer): def __init__(self, *layers): super().__init__() self.layers = layers for layer in layers: self.parameters.extend(layer.parameters) def forward(self, X): backprops = [] Y = X for layer in self.layers: Y, backprop = layer.forward(Y) backprops.append(backprop) def backward(D): for backprop in reversed(backprops): D = backprop(D) return D return Y, backward
正如我们前面提到的,我们将需要定义批样本的损失函数和梯度。一个典型的例子是MSE,它被常用在回归问题里,我们可以这样实现它:
def mse_loss(Yp, Yt): diff = Yp - Yt return np.square(diff).mean(), 2 * diff / len(diff)
就差一点了!现在,我们定义了两种层,以及合并它们的方法,下面如何训练呢?我们可以使用类似于scikit-learn或者Keras中的API。
class Learner(): def __init__(self, model, loss, optimizer): self.model = model self.loss = loss self.optimizer = optimizer def fit_batch(self, X, Y): Y_, backward = self.model.forward(X) L, D = self.loss(Y_, Y) backward(D) self.model.update(self.optimizer) return L def fit(self, X, Y, epochs, bs): losses = [] for epoch in range(epochs): p = np.random.permutation(len(X)) X, Y = X[p], Y[p] loss = 0.0 for i in range(0, len(X), bs): loss += self.fit_batch(X[i:i + bs], Y[i:i + bs]) losses.append(loss) return losses
这就行了!如果你跟随着我的思路,你可能就会发现其实有几行代码是可以被省掉的。
这代码能用不?
现在可以用一些数据测试下我们的代码了。
X = np.random.randn(100, 10)w = np.random.randn(10, 1)b = np.random.randn(1)Y = X @ W + Bmodel = Linear(10, 1)learner = Learner(model, mse_loss, SGDOptimizer(lr=0.05))learner.fit(X, Y, epochs=10, bs=10)
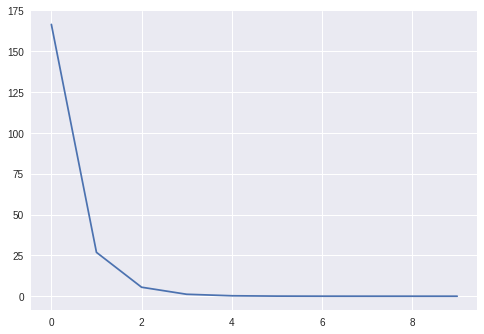
我一共训练了10轮。
我们还能检查学到的权重和真实的权重是否一致。
print(np.linalg.norm(m.weights.tensor - W), (m.bias.tensor - B)[0])> 1.848553648022619e-05 5.69305886743976e-06
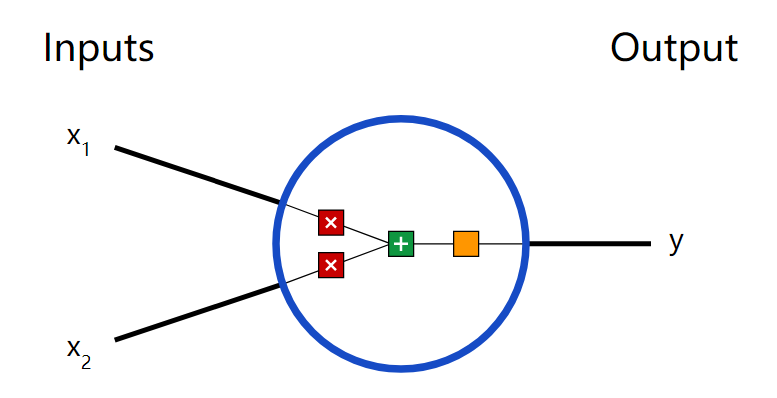
好了,就这么简单。让我们再试试非线性数据集,例如y=x1x2,并且再加上一个Sigmoid非线性层和另一个线性层让我们的模型更复杂些。像下面这样:
X = np.random.randn(1000, 2)Y = X[:, 0] * X[:, 1]losses1 = Learner( Sequential(Linear(2, 1)), mse_loss, SGDOptimizer(lr=0.01)).fit(X, Y, epochs=50, bs=50)losses2 = Learner( Sequential( Linear(2, 10), Sigmoid(), Linear(10, 1) ), mse_loss, SGDOptimizer(lr=0.3)).fit(X, Y, epochs=50, bs=50)plt.plot(losses1)plt.plot(losses2)plt.legend(['1 Layer', '2 Layers'])plt.show()
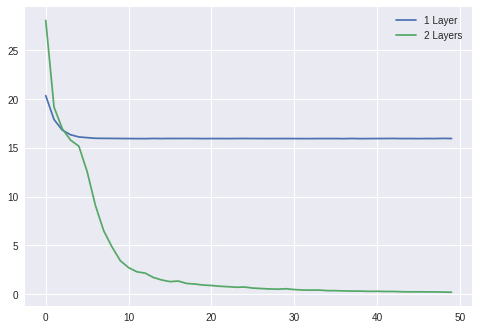
比较单一层vs两层模型在使用sigmoid激活函数的情况下的训练损失。
-
神经网络
+关注
关注
42文章
4772浏览量
100845 -
代码
+关注
关注
30文章
4791浏览量
68694 -
python
+关注
关注
56文章
4797浏览量
84756
原文标题:100行Python代码,轻松搞定神经网络
文章出处:【微信号:BigDataDigest,微信公众号:大数据文摘】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
【PYNQ-Z2试用体验】神经网络基础知识
卷积神经网络如何使用
【案例分享】ART神经网络与SOM神经网络
如何构建神经网络?
不可错过!人工神经网络算法、PID算法、Python人工智能学习等资料包分享(附源代码)
如何提升AI算法速度 打造接近人脑规模的神经网络
用Python从头实现一个神经网络来理解神经网络的原理1
用Python从头实现一个神经网络来理解神经网络的原理2
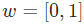
用Python从头实现一个神经网络来理解神经网络的原理3

用Python从头实现一个神经网络来理解神经网络的原理4





 100行Python代码 轻松搞定神经网络
100行Python代码 轻松搞定神经网络










评论