前面两篇文章讲了离散傅里叶变换的应用之一——用FFT分析信号频谱,并给出了一道题目。链接如下:
数字信号处理系列串讲第11篇(离散信号的频域分析之五)——傅里叶变换的应用(1):FFT分析信号频谱(之一)
数字信号处理系列串讲第12篇(离散信号的频域分析之五)——FFT分析信号频谱题目解答(补充修订版)
今天这篇,来说一说FFT分析信号频谱中一个重要的概念:频率分辨率。
分辨率是信号处理中的基本概念之一,通俗地讲,分辨率就是能够将两个事物分开的能力。频率分辨率就是频域上能够将两个不同频率分量分开的能力。
前面说了,计算机只能处理有限长的数据。无限长的单频信号的频谱为一个冲激,但有限长(例如长度为L)的单频信号,频谱是什么样子呢?上一篇中已经给大家详细推导了,宽度为4Π/L(单位:弧度rad)。那么,如果信号中包含两个频率成分,要能够把它们分开,它们最近能离得多近呢?看下图:
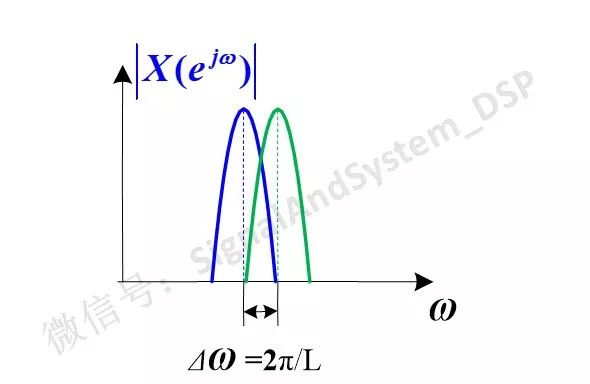
图1
注意,上图中只画出了主瓣,没有画出旁瓣。上图中的Δw为数字域频率,单位为:弧度rad,再利用数字域频率与模拟角频率的关系(如果这个问题有疑惑,看如下链接:)
数字信号处理系列(离散信号的频域分析之二)——数字域频率与模拟角频率
得到频率分辨率为:
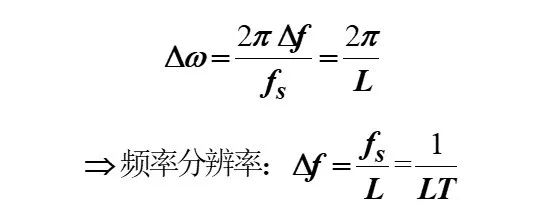
图2
上式中,fs为采样率,T为采样间隔,L为截取的数据点数。因此,LT为数据时间长度(单位:秒),也就是说
频率分辨率为信号时长的倒数。
这与我们的直观感受也是一致的,截取的信号时间越长,得到的信息越多,频率分辨率越高,即Δf的数值越小,越有可能把离得很近的两个频率分辨开。
那么,问题来了,如果L很小,但我给截取后的数据补上很多个零,做一个比较大点数的DFT,能提高频率分辨率吗?
补零的作用,可以减小将频谱离散化时的间隔(提高频谱离散化的精细度,因为N点DFT就是将频谱以2Π/N为间隔离散化),可以减小”栅栏效应“。但DFT是对信号DTFT的抽样,而补零并不能改变DTFT的结果,也就是说,连续的频谱在补零前后是一样的,因此频率分辨率也就不会发生改变。
另一方面,从信息的角度,直观上就很容易理解,补零并不增加新的信息,自然也就不会改善频率分辨率。
所以说,对L点长的数据做N点DFT,频率分辨率为:fs/L,而不是fs/N。
但是,在计算第k根谱线对应的模拟频率时,是:kfs/N,而不是kfs/L。
为了区分,有些教材上,将fs/N称为“计算分辨率”,fs/L称为”物理分辨率“。
我讲清楚了吗?
另外,我们知道,如果采样率为fs,意味着信号中最高频率fh不能超过fs的一半,即:
fs≥2fh
将上式代入到图2公式中,得到:
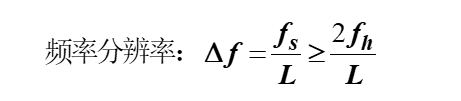
根据上式,得到:
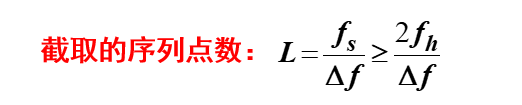
也就是说,若信号中最高频率成分为fh,要达到Δf的频率分辨率,至少要截取的序列点数L为2fh/Δf。
注意,上式得到的L,为理论上的最低条件。因为上式的导出,是没有考虑其他信号处理措施(如加各种窗),除了矩形窗之外的窗函数,主瓣会展宽,而且实际信号含有噪声。因此,实际信号处理时,序列点数需大于上述条件。
最后,总结一下重点:
频率分辨率为信号时长的倒数。
补零,可以改善“栅栏效应”,但不能真正提高信号的频率分辨率。
-
FFT
+关注
关注
15文章
438浏览量
59675 -
频率分辨率
+关注
关注
0文章
2浏览量
6954
原文标题:数字信号处理系列串讲第13篇(离散信号的频域分析之五)——傅里叶变换的应用(1):FFT分析信号频谱(之二)
文章出处:【微信号:SignalAndSystem_DSP,微信公众号:信号与系统和数字信号处理】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐




 傅里叶变换的应用 FFT分析信号频谱
傅里叶变换的应用 FFT分析信号频谱











评论