神经网络如何正确初始化?

初始化对训练深度神经网络的收敛性有重要影响。简单的初始化方案可以加速训练，但是它们需要小心避免常见的陷阱。

近期，deeplearning.ai就如何有效地初始化神经网络参数发表了交互式文章，图灵君将结合这篇文章与您一起探索以下问题：

1、有效初始化的重要性

2、梯度爆炸或消失的问题

3、什么是正确的初始化？

4、Xavier初始化的数学证明

一、有效初始化的重要性

要构建机器学习算法，通常需要定义一个体系结构（例如Logistic回归，支持向量机，神经网络）并训练它来学习参数。 以下是神经网络的常见训练过程：

1、初始化参数

2、选择优化算法

3、重复这些步骤：

a、正向传播输入

b、计算成本函数

c、使用反向传播计算与参数相关的成本梯度

d、根据优化算法，使用梯度更新每个参数

然后，给定一个新的数据点，您可以使用该模型来预测它的类。

初始化步骤对于模型的最终性能至关重要，它需要正确的方法。 为了说明这一点，请考虑下面的三层神经网络。 您可以尝试使用不同的方法初始化此网络，并观察它对学习的影响。

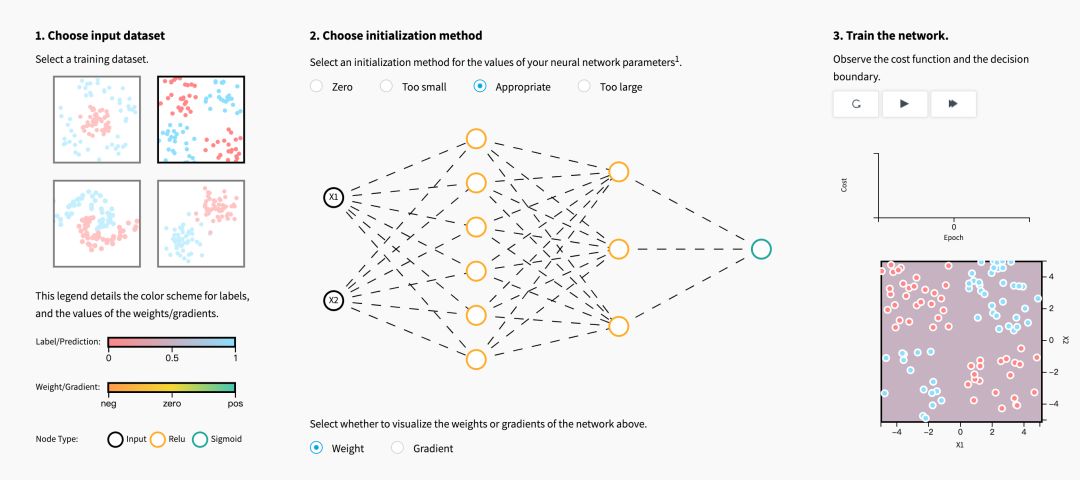
当初始化方法为零时，对于梯度和权重，您注意到了什么?

用零初始化所有权重会导致神经元在训练期间学习相同的特征。

实际上，任何常量初始化方案的性能表现都非常糟糕。 考虑一个具有两个隐藏单元的神经网络，并假设我们将所有偏差初始化为0，并将权重初始化为一些常数α。 如果我们在该网络中正向传播输入（x1，x2），则两个隐藏单元的输出将为relu（αx1+αx2）。 因此，两个隐藏单元将对成本具有相同的影响，这将导致相同的梯度。

因此，两个神经元将在整个训练过程中对称地进化，有效地阻止了不同的神经元学习不同的东西。

在初始化权重时，如果值太小或太大，关于成本图，您注意到了什么?

尽管打破了对称性，但是用值（i）太小或（ii）太大来初始化权重分别导致（i）学习缓慢或（ii）发散。

为高效训练选择适当的初始化值是必要的。我们将在下一节进一步研究。

二、梯度的爆炸或消失问题

考虑这个9层神经网络。

在优化循环的每次迭代（前向，成本，后向，更新）中，我们观察到当您从输出层向输入层移动时，反向传播的梯度要么被放大，要么被最小化。 如果您考虑以下示例，此结果是有意义的。

假设所有激活函数都是线性的（标识函数）。 然后输出激活是：

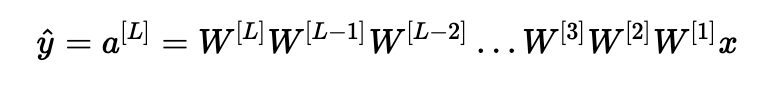
其中，L=10,W[1],W[2],…,W[L−1]都是大小为(2,2)的矩阵，因为层[1]到[L-1]有2个神经元，接收2个输入。考虑到这一点，为了便于说明，如果我们假设W[1]=W[2]=⋯=W[L−1]=W，输出预测是y^=W[L]WL−1x（其中WL−1将矩阵W取为L-1的幂，而W[L]表示Lth矩阵）。

初始化值太小，太大或不合适的结果是什么？

情形1：过大的初始化值会导致梯度爆炸

考虑这样一种情况:初始化的每个权重值都略大于单位矩阵。

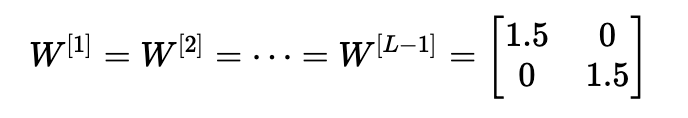
这简化为y^=W[L]1.5L−1x，并且a[l]的值随l呈指数增加。 当这些激活用于反向传播时，就会导致梯度爆炸问题。 也就是说，与参数相关的成本梯度太大。 这导致成本围绕其最小值振荡。

情形2：初始化值太小会导致梯度消失

类似地，考虑这样一种情况:初始化的每个权重值都略小于单位矩阵。

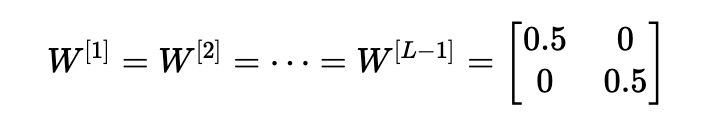
这简化为y^=W[L]0.5L−1x，并且激活a [l]的值随l呈指数下降。 当这些激活用于反向传播时，这会导致消失的梯度问题。 相对于参数的成本梯度太小，导致在成本达到最小值之前收敛。

总而言之，使用不适当的值初始化权重将导致神经网络训练的发散或减慢。虽然我们用简单的对称权重矩阵说明了梯度爆炸/消失问题，但观察结果可以推广到任何太小或太大的初始化值。

三、如何找到合适的初始化值

为了防止网络激活的梯度消失或爆炸，我们将坚持以下经验法则：

1、激活的平均值应为零。

2、激活的方差应该在每一层保持不变。

在这两个假设下，反向传播的梯度信号不应该在任何层中乘以太小或太大的值。 它应该移动到输入层而不会爆炸或消失。

更具体地考虑层l， 它的前向传播是：

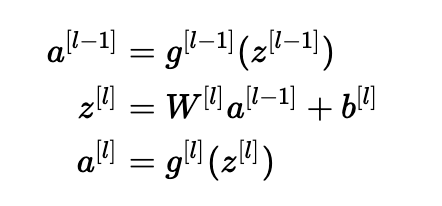
我们希望以下内容：

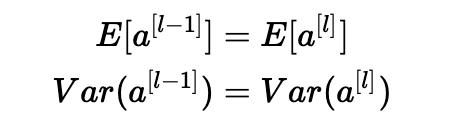
确保零均值并保持每层输入方差的值不会产生爆炸/消失信号，我们稍后会解释。 该方法既适用于前向传播（用于激活），也适用于反向传播传播（用于激活成本的梯度）。 推荐的初始化是Xavier初始化（或其派生方法之一），对于每个层l：

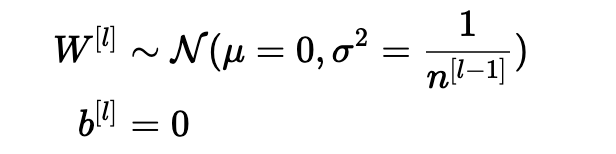
换句话说，层l的所有权重是从正态分布中随机选取的，其中均值μ= 0且方差σ2= n [l-1] 1其中n [l-1]是层l-1中的神经元数。 偏差用零初始化。

下面的可视化说明了Xavier初始化对五层全连接神经网络的每个层激活的影响。

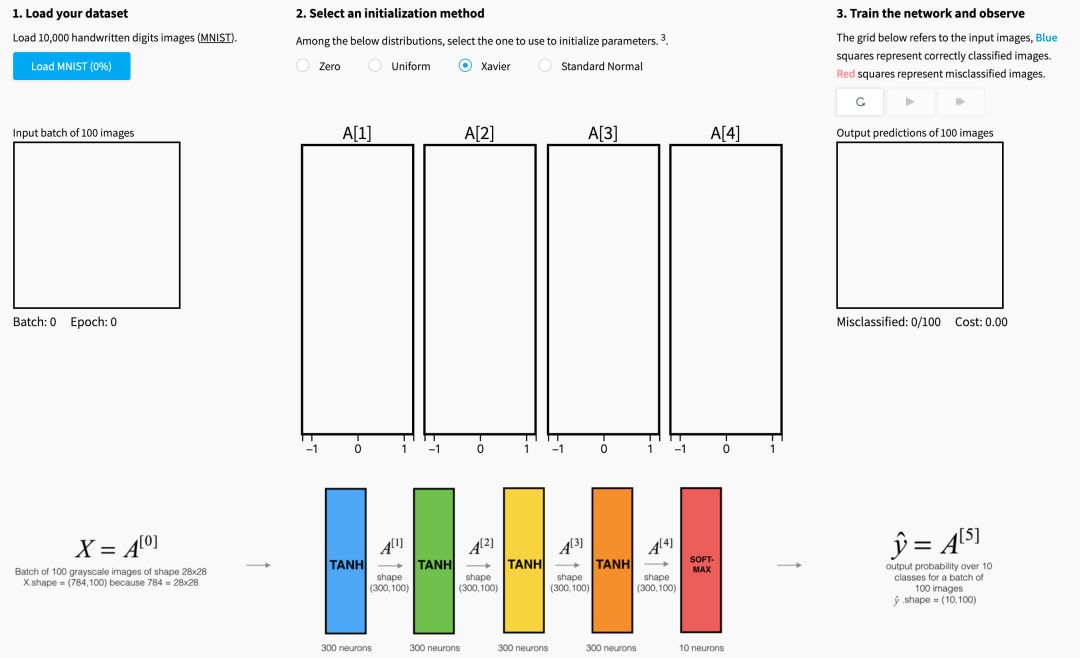
您可以在Glorot等人中找到这种可视化背后的理论。（2010年）。 下一节将介绍Xavier初始化的数学证明，并更准确地解释为什么它是一个有效的初始化。

四、Xavier初始化的合理性

在本节中，我们将展示Xavier初始化使每个层的方差保持不变。 我们假设层的激活是正态分布在0附近。 有时候，理解数学原理有助于理解概念，但不需要数学，就可以理解基本思想。

让我们对第（III）部分中描述的层l进行处理，并假设激活函数为tanh。 前向传播是：

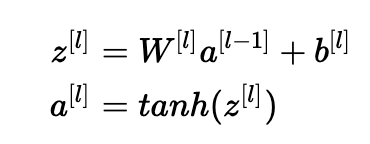
目标是导出Var（a [l-1]）和Var（a [l]）之间的关系。 然后我们将理解如何初始化我们的权重，使得：Var(a[l−1])=Var(a[l])。

假设我们使用适当的值初始化我们的网络，并且输入被标准化。 在训练初期，我们处于tanh的线性状态。 值足够小，因此tanh(z[l])≈z[l]，意思是：

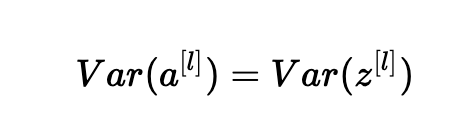
此外，z[l]=W[l]a[l−1]+b[l]=向量(z1[l],z2[l],…,zn[l][l])其中zk[l]=∑j=1n[l−1]wkj[l]aj[l−1]+bk[l]。 为简单起见，我们假设b[l]=0（考虑到我们将选择的初始化选择，它将最终为真）。 因此，在前面的方程Var(a[l−1])=Var(a[l])中逐个元素地看，现在给出：

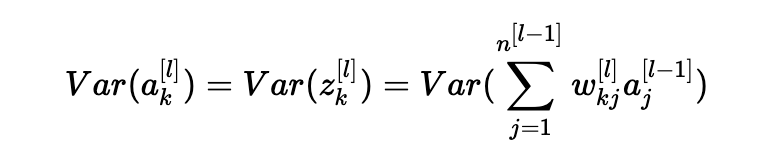
常见的数学技巧是在方差之外提取求和。 为此，我们必须做出以下三个假设：

1、权重是独立的，分布相同；

2、输入是独立的，分布相同；

3、权重和输入是相互独立的。

因此，现在我们有：

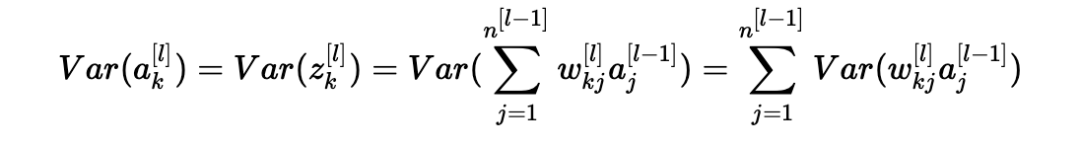
另一个常见的数学技巧是将乘积的方差转化为方差的乘积。公式如下:

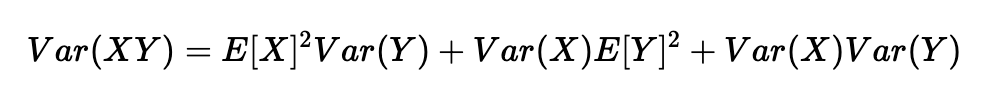
使用X=wkj[l]和Y=aj[l−1]的公式，我们得到：

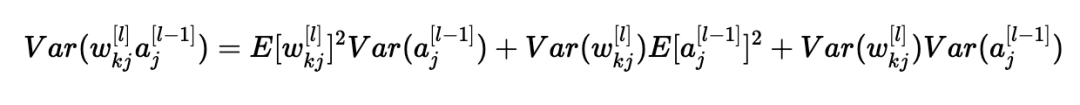
我们差不多完成了！ 第一个假设导致E[wkj[l]]2=0，第二个假设导致E[aj[l−1]]2=0，因为权重用零均值初始化，输入被归一化。 从而：

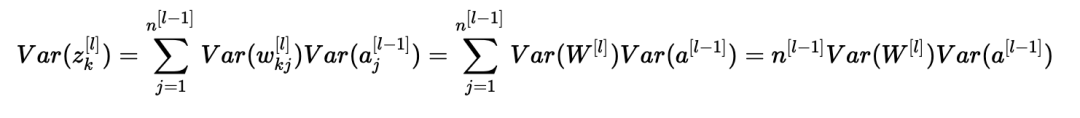
上述等式源于我们的第一个假设，即:

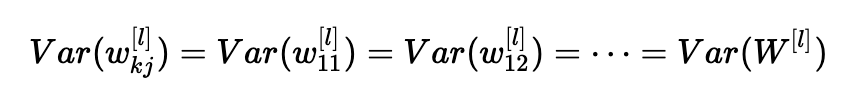
同样，第二个假设导致：

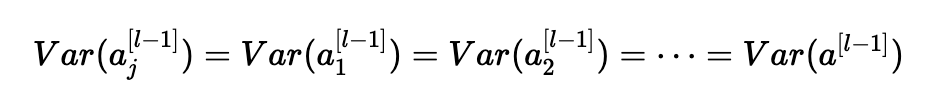
同样的想法：

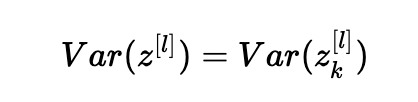
总结一下，我们有:

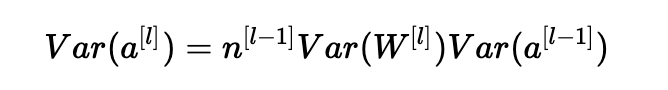
瞧！ 如果我们希望方差在各层之间保持不变(Var(a[l])=Var(a[l−1]))，我们需要Var(W[l])=n[l−1]1。 这证明了Xavier初始化的方差选择是正确的。

请注意，在前面的步骤中，我们没有选择特定的层ll。 因此，我们已经证明这个表达式适用于我们网络的每一层。 让LL成为我们网络的输出层。 在每一层使用此表达式，我们可以将输出层的方差链接到输入层的方差：

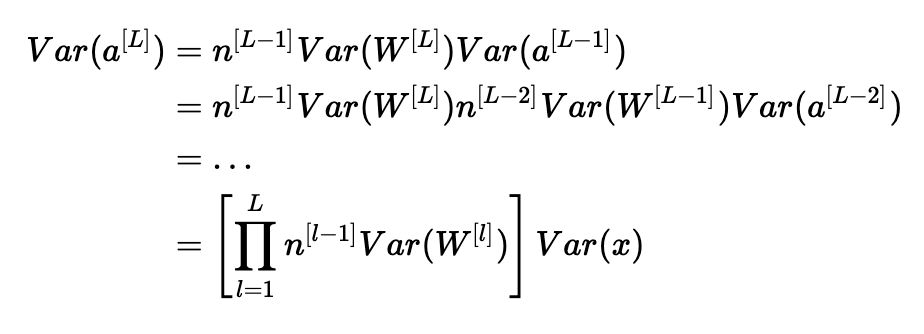
根据我们如何初始化权重，我们的输出和输入的方差之间的关系会有很大的不同。 请注意以下三种情况。

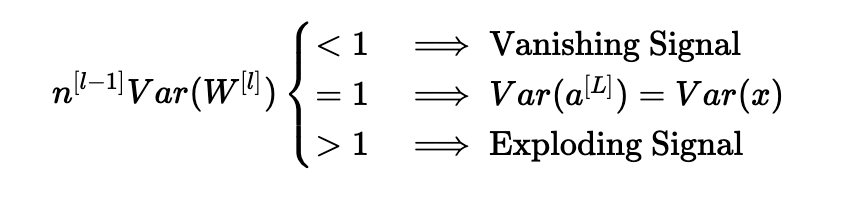
因此，为了避免正向传播信号的消失或爆炸，我们必须通过初始化Var(W[l])=n[l−1]1来设置n[l−1]Var(W[l])=1。

在整个证明过程中，我们一直在处理在正向传播期间计算的激活。对于反向传播的梯度也可以得到相同的结果。这样做，您将看到，为了避免梯度消失或爆炸问题，我们必须通过初始化Var(W[l])=n[l]1来设置n[l]Var(W[l])=1。

结论

实际上，使用Xavier初始化的机器学习工程师会将权重初始化为N(0,n[l−1]1)或N(0,n[l−1]+n[l]2)。 后一分布的方差项是n [l-1] 1和n [1] 1的调和平均值。

这是Xavier初始化的理论依据。 Xavier初始化与tanh激活一起工作。 还有许多其他初始化方法。 例如，如果您正在使用ReLU，则通常的初始化是He初始化（He et al，Delving Deep into Rectifiers），其中权重的初始化方法是将Xavier初始化的方差乘以2。虽然这种初始化的理由稍微复杂一些，但它遵循与tanh相同的思考过程。