摘要
针对在具有重叠结构的透明矩形中寻找木偶这一问题,Hinton大神想到使用松弛算法,通过从冲突局部解释网络中提取全局最佳图形的方式找木偶。
介绍
该程序的输入是透明矩阵的四个角坐标,见图1。要找到木偶模型的最佳实例化的难点在于,如果我们只考虑一个矩形及其重叠的矩形,那么每个矩形可以是几个不同的子木偶组成或者根本不存在子木偶,所以必须通过找到全局最优解释,来解决局部模糊性的问题。
本文作者介绍了如何使用松弛方法,而不是将所有局部可解释的空间组合进行显式搜索。松弛方法有以下几个优点:
1.利用并行计算可以快速地找到全局最优解释。在计算局部可能的数量上,需要的时间不是指数级的,因为组合没有被显式处理。
2.所需的计算空间只随着可移植性的数量线性增加,这使得该方法优于全局搜索和宽度优先并行搜索方法,并且宽度优先并行搜索方法存在组合爆炸的问题。
3.该方法提供了全局最优解释,而不仅仅是像启发式搜索那样只是得到一个可用的解释。

图1a 有一些额外矩形的木偶

图1b 使用松弛方法之前和之后的矩形的局部假设。第二列表示图片的方向,直接相关的感知在下一列显示。
木偶模型
该木偶由 15 个矩形部件组成,具有如下性质和关系:
1.每一部分都有近端和远端。其中近端是指最接近头顶的一端。对于每个部件,沿近-远轴的长度必须大于其宽度。
2.躯干必须比所有的上肢部件都要宽,而每一个上肢部件又必须比与其相连的下肢部件宽。此外,头部必须比颈部宽。
3.头部的面积必须大于颈部,下肢面积必须大于双手或双脚。
4.相连的部件必须以正确的方式重叠。每个部件只能指定一个区域是否重叠,而不能指定多个区域。大腿和小腿之间连接的规范如图2所示,图2c展示了一些正确重叠的例子和存在近似误差的例子。

图2a 四个区域的感知

表2b 展示膝盖区域关系的定义

图2c 两个令人满意的膝关节例子(上)和三个有近似误差的例子(下)。箭头表示远端+近端方向。大腿总是这两条腿中较宽的那条。
木偶模型是非常随意的,但是必须使用比简单连接更复杂的规则来避免出现如图3所示的情况。一种比较灵活的方式是只要其余部件仍是合理的,允许扩展一些连接或比例。这方面的影响将会在后面进行讨论。

图3 一种矩形的配置,具有与木偶相同的连通性图,但具有不同的关系和比例
不完全木偶
感知器是一种数据结构,该数据结构可以表示木偶部件的矩形解释,并且有插槽,该插槽被其他相关联的感知器所填充。关联关系也由数据结构显式地表示,数据结构有两个点,每个点对应一个相关的感知器。
当图中没有完整的木偶时,会发现存在不完整的木偶,即一些感知器中有空插槽的木偶。如果给程序一些评估不完整木偶的方法,那么它可以做同样的事情,这样当有更好的选择时,它就可以避免糟糕的全局解释。目前,满足以下约束条件,并且拥有最多关联关系则被定义为最好的木偶:
1.一个矩形只能表示一个部件。
2.除了大腿和上臂可以有两个插槽外,没有一个插槽可以由多个关系填充。
3. 任何类型的部件被实例化的次数都不能超过它在模型中出现的次数,例如,不能有两条以上的大腿。
4.除非感知器存在,否则关系不存在。
改善局部网络结构
由于木偶的潜在不完整性导致很难排除局部的任何感知,因此采用替代方法,从强烈暗示特定感知器的局部配置开始管理它们。在这些核心元素中,通过尝试填充与已存在的感知相关的空闲时隙来增长网络。
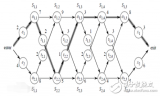
如果这样做失败了,并且有合适的重叠矩形,则使用与新创建的感知器的关系,而这些新感知器的其他槽作为进一步的生长点。如果模型的最佳实例化至少包含一个核心元素,则生成的网络将包含所有必需的感知器。它还将包含许多其他的槽,一些槽将由几个竞争关系来填充,见图1b。然而,一般来说,以这种方式发展起来的网络要比由所有局部可能性组成的网络小得多。
感知器之间的相互作用
并行处理必须生成非常多的局部可能性结果以确保生成正确的可能性结果,因此除非有快速排除不正确结果的方法,否则将不具有并行计算的时间优势。简单的本地竞争是行不通的,因为正确的感知有时会有一个更好的局部选择。但是如果感知器也被允许通过他们的关系互相帮助,那么可能会通过网络传播来帮助一个全局一致但局部较差的感知,见图4。
这种类型的系统,其中全局模式从局部相互作用中产生,作为格式塔现象的基础是有吸引力的,但如果系统快速达到稳定状态并且有一些最佳模式出现,那么这种系统很有意义。
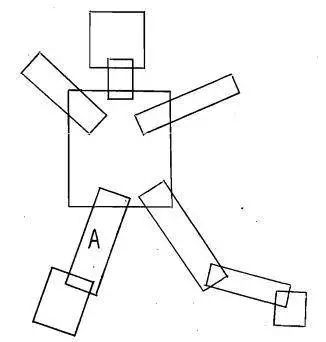
图4 松弛法是将A解释为大腿,而局部最优选择的结果是小腿。
偏好约束网络
找到最好的木偶,相当于要从节点是感知器的网络中提取,并且关要满足某些约束的最佳子网。如果子网的值可以表示为其各个节点的首选项的和,并且如果约束等于可能状态空间中的超平面,则可以使用松弛方法。每个节点都有一个介于0和1之间的实数,也即可信度。
该值不应与偏好相混淆,可以解释为节点正确的概率,即最佳一致子网的一部分。约束条件是可信度之间的不等式。例如,n或m表示为 ,其中c(n)是节点n的可信度。
,其中c(n)是节点n的可信度。
节点的可信度可以表示为多维空间的轴。可信度分布是空间中的一个点,是对每个平面的响应。为了满足不等式约束条件,一个点必须位于相关的超平面或其一侧。满足所有约束条件的状态称为合法状态,超出空间区域就是凸多面体,因为它是超平面和半空间的交集。
应用关系到木偶图片
对于木偶中不完整的部分,给出了对该木偶最佳实例化的定义。关于可信度的约束条件表达式如下:
1.矩形的感知关系式: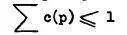
2.竞争关系表达式:
3.模型中出现n次部件的感知关系式:
4.两个感知器p,q之间的关系式:
讨论
用来揭示松弛法原理的任务,在许多方面都得到了简化。一个容易改进的点是缺乏对膝关节和肘关节连接角度的关注。一个好的木偶模型需要肘部向一个方向弯曲,膝盖能向另一个方向弯曲,从而利用这些知识,制造出更好的木偶。这种类型的约束的理论意义在于它是非局部的,就像对于上下文无关语句来说数字一致性规范是存在问题的(Lyons 1968)。
针对上述问题,解决方法是引入全局节点来表示木偶的边。这些边节点之间通过排他或约束进行相互关联,每个关联通过物体隐含约束条件关联到其他全局边节点。现在最好的实例是有兼容的膝部和肘部。
某情况下,这是一个太过苛刻的约束条件,因为在现实中有折断的胳膊肘总比没有的好。因此,作者引入了没有额外限制的可选弱关联,这样会和有较强关联的相互冲突。所以,如果有更好的偏好设置,好的手肘要优于差的手肘,但是差的手肘不会优于任何其他手肘。
-
矩阵
+关注
关注
0文章
423浏览量
34579 -
模型
+关注
关注
1文章
3262浏览量
48916 -
感知器
+关注
关注
0文章
34浏览量
11849
原文标题:找啊找啊找木偶,图灵奖得主G. Hinton第一篇论文曝光!
文章出处:【微信号:rgznai100,微信公众号:rgznai100】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
LabVIEW结构的使用——全局变量和局部变量
静态变量、全局变量和局部变量
FPGA全局复位及局部复位设计分享
【原创分享】STM32 C语言全局变量和局部变量
如何以编程方式从STL库中提取版本信息?
如何通过M480系列的PDMAA步态模式从RGB颜色阵列中提取
在LV中提取图形及前面板的方法
arm技术在PDF中提取图形的方法
全局变量和局部变量有什么区别
新加坡研发从空气中提取水的气凝胶
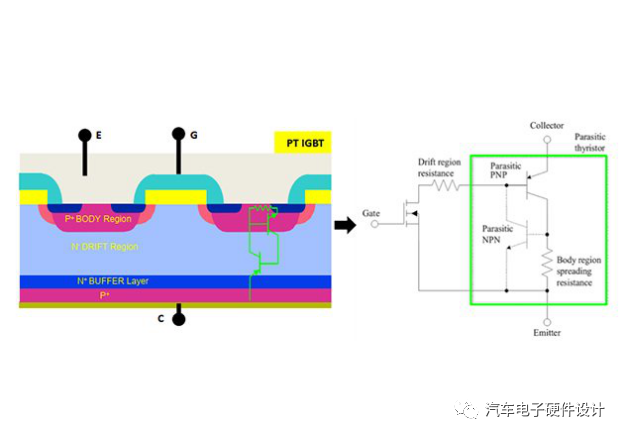
IPM如何从可用的IGBT器件中提取最佳性能?




 从冲突局部解释网络中提取全局最佳图形的方式找木偶
从冲突局部解释网络中提取全局最佳图形的方式找木偶










评论