谷歌开源张量网络库TensorNetwork，GPU处理提升100倍！

世界上许多最严峻的科学挑战，如开发高温超导体和理解时空的本质，都涉及处理量子系统的复杂性。然而，这些系统中量子态的数量程指数级增长，使得暴力计算并不可行。为了解决该问题，数据结构采用了张量网络的方式。张量网络让人们关注与现实世界问题最相关的量子态，如低能态。张量网络已经越来越多地在机器学习中得到应用。

然而，目前仍存在相当多的一些挑战阻碍了其在机器学习社区中的广泛使用：1）用于加速硬件的生产级张量网络库还不能用于大规模运行张量网络算法；2）大多数张量网络文献是面向物理应用的，并产生了一种错误的印象，即需要量子力学方面的专业知识来理解算法。

为了解决这一问题，谷歌 X 实验室与加拿大Perimeter理论物理研究所（Perimeter Institute for Theoretical Physics ）的研究人员合作开发了张量网络 TensorNetwork，以 TensorFlow 作为后端，针对 GPU 处理进行了优化。与在 CPU 上计算工作相比，可以实现高达 100 倍的加速。这是一个全新的开源库，旨在提高张量计算的效率。

据悉，研究人员已经发布了一些列论文对张量网络的概念、特性以及应用特例等方面进行了详细阐释。

工作原理

张量是一种多维数组，按照顺序进行分类。例如，一个普通数零阶张量，也称为标量，一个向量是一阶张量，一个矩阵是二阶张量。虽然低阶张量可以很容易地用数字数组或像 Tijnklm 这样的数学符号来表示，但一旦开始讨论高阶张量，这个符号就变得非常麻烦。

这一点上，使用图解记数法是非常有用的，在这种记数法中，人们只需画一个有许多条线或” 腿 “的圆（或其他形状）。在这个符号中，标量只是一个圆，向量只有一条腿，矩阵有两条腿等。张量的每条腿也有大小，也就是腿的长度。

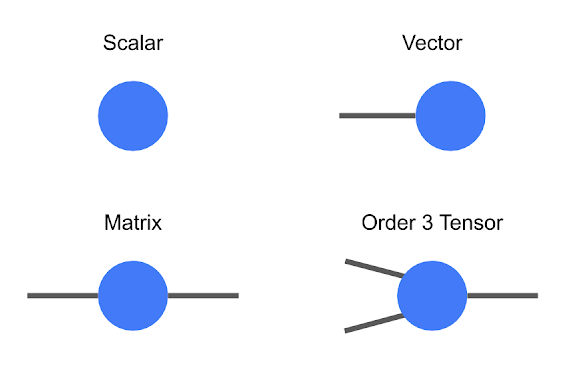
张量的图解符号

以这种方式表示张量的好处是简洁地编码数学运算，例如，将一个矩阵乘以一个向量得到另一个向量，或者两个向量相乘得到标量。这个过程被称为张量收缩。

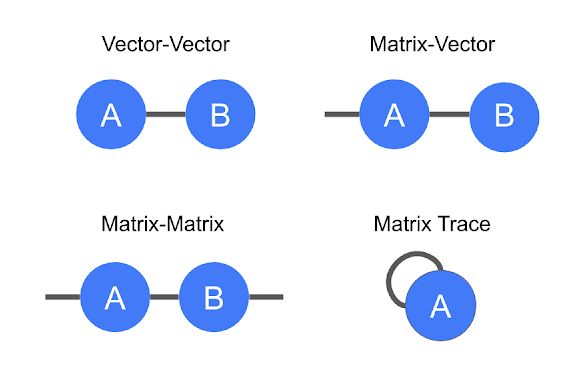
张量收缩的图解表示法

向量和矩阵乘法以及矩阵迹线（即矩阵对角元素的总和）。

除了这些案例之外，还有以张量收缩模式进行编码以形成一个新张量的图形方式。每个组成张量都有一个由自己的腿数决定的顺序。连接的腿在图中形成一条边，代表收缩，而剩余悬空腿的数量决定了合成张量的顺序。

左：四个矩阵乘积的表示，即 tr（ABCD），它是一个标量。右：三个三阶张量收缩，三条腿悬空，产生一个新的三阶张量。

虽然这些例子非常简单，但张量网络通常代表以各种方式收缩的数百个张量。用传统的符号来描述这样一件事情是非常模糊的，这也是 Roger Penrose 在 1971 年发明图解符号（diagrammatic notation）的原因。

实践过程

以一些黑白图像为例，每个图像可以被看做是 N 个像素值的列表。单个图像中的单个像素可以被独热编码（ one-hot-encoding）成二维向量，并且通过这些像素编码组合在一起，我们可以得到 2N 个维独热编码的结果。我们可以将高维向量转化为 N 阶张量，然后将图像集合中所有张量相加，得到量 Ti1，i2，...，iN 的集合。

这听起来像是一件非常浪费时间的事情。因为以这种方式对约 50 像素的图像进行编码已经占用了数千兆字节的内存。这正是张量网络的作用所在。研究人员没有直接存储或操纵张量 T，而是将张量 T 作为张量网络内的多个小的张量组合。结果证明这非常有效。例如，流行的矩阵乘积态（matrix product state，MPS）网络可以将 T 表示为 N 个较小的张量，从而总参数量为 N 的线性级，而不是指数级。

高阶张量 T 用矩阵乘积态张量网络中的许多低阶张量来表示。

但在有效构建或操纵大型张量网络的同时又能始终避免使用大量内容的需求，是不太明显的。但事实证明，这在许多情况下是可能的，这也是张量网络广泛用于量子物理和机器学习领域的原因。Stoudenmire 和 Schwab 使用这种编码来构建图像分类模型，展示了张量网络的新用途。而 TensorNetwork 库旨在推进这类工作，研究人员在 TensorNetwork 相关论文中介绍了该库如何应用于张量网络的操作。

在物理场景中的应用性能

TensorNetwork 是一个针对张量网络算法的通用库，因此它适用于物理学场景。逼近量子态是张量网络在物理学中的一个典型用例，可说明张量网络库的能力。在另一篇论文《TensorNetwork on TensorFlow: A Spin Chain Application Using Tree Tensor Networks》中，研究人员提出了一种近似树张量网络（tree tensor network，TTN），并使用张量网络库实现了该算法。此外，研究人员还对比了 CPU 和 GPU 的情况，发现在使用 GPU 和张量网络库时，计算速度显著提高了近 100 倍。

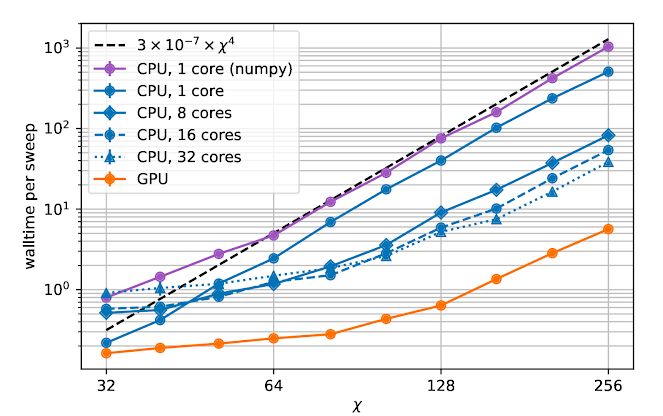
计算时间作为连接维度的函数 X。连接维度（ bond dimension ）决定了张量网络中张量的大小。连接维度越大意味着张量网络约强大，但这个过程也需要更多的计算资源。

总结及未来工作

本文是讲述 TensorNetwork 实际应用案例的第一篇文章，后续的论文中，研究人员将使用 TensorNetwork 在 MNIST 和 Fashion-MNIST 上执行图像分类，后面还将包括时序分析、量子电路仿真等。研究人员希望 TensorNetwork 能成为物理学家和机器学习从业者的宝贵工具。