电感器可以串联连接在一起,当它们以菊花链形式连接在一起共享一个共同的电流时
这些电感器的互连会产生更复杂的网络,其整体电感是个体的组合电感器。然而,有一些串联或并联电感器的规则,这是基于各个电感器之间不存在互感或磁耦合的事实。
据说电感器连接在“系列”中当它们以直线菊花链式连接在一起时,端到端。在系列电阻器教程中,我们看到串联连接在一起的电阻的不同值只是“加”在一起,电感也是如此。串联电感简单地“加在一起”,因为线圈匝数有效增加,总电路电感L T 等于加在一起的所有单个电感的总和。
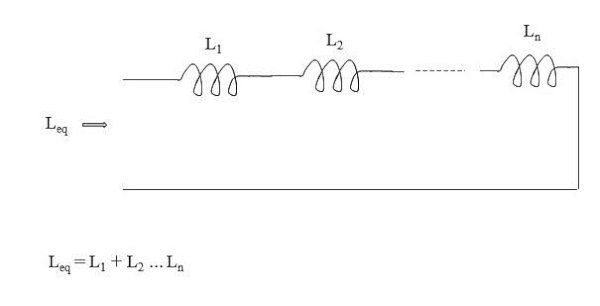
串联电路中的电感

当前,( I )流过第一个电感器, L 1 没有别的办法可以通过第二个电感器和第三个电感器,依此类推。然后,串联电感有一个公共电流流过它们,例如:
I L1 = I L2 = I L3 = I AB ... etc。
In上面的例子,电感 L 1 , L 2 和 L 3 在 A 和 B 之间串联连接在一起。使用基尔霍夫电压定律(KVL)可以找到每个电感上各个电压降的总和,其中, V T = V 1 + V 2 + V 3 我们从之前的电感教程中了解到电感上的自感电动势如下: V = Ldi / dt 。
因此,在上面的示例中,通过获取每个电感上各个电压降的值,系列组合的总电感如下:

通过上面的等式除以 di / dt ,我们可以减少它,以给出计算总电感的最终表达式将电感串联在一起时的电路,如下所示:
串联方程中的电感
L total = L 1 + L <子> 2 + L <子> 3 + ... .. + L <子>名词 等
然后通过简单地将个体加在一起就可以找到串联链的总电感串联电感器的导管就像串联电阻一样。然而,只有当两个或多个电感器之间存在“无”互感或磁耦合时,上述方程才成立(它们彼此磁隔离)。
要记住的一个重要点串联电路中的电感器,串联连接在一起的任何两个或多个电感器的总电感( L T )总是GREATER串联电感器中最大的电感器
串联电感器实例No1
三个10mH,40mH和50mH的电感器串联组合在一起,两者之间没有互感。计算串联组合的总电感。

串联互连电感
当电感串联在一起时为了使一个磁场与另一个磁场相连,互感的效果要么根据磁耦合量增加或减少总电感。这种互感的影响取决于线圈的距离和它们彼此的方向。
相互连接的串联电感可以归类为“辅助”或“反对”总电感。如果由电流产生的磁通量以相同方向流过线圈,则称线圈累积耦合。如果电流以相反的方向流过线圈,那么线圈被称为差分耦合,如下所示。
累积耦合串联电感
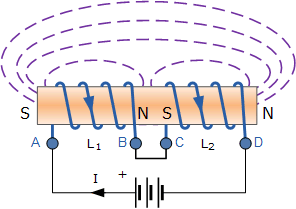
虽然通过两个累积耦合线圈在A点和D点之间流动的电流方向相同,但需要修改上述每个线圈电压降的公式。由于互感的影响,考虑了两个线圈之间的相互作用。每个单独线圈的自感, L 1 和 L 2 分别与以前相同,但是增加 M 表示互感。
然后,累积耦合线圈中的总电动势被给出为:

其中: 2M 表示线圈 L 1 对的影响> L 2 ,同样在 L 1 上线圈 L 2 。
通过上面的公式除以 di / dt ,我们可以减小它,以给出电感累积连接时计算电路总电感的最终表达式给出如下:
L total = L 1 + L 2 + 2M
如果其中一个线圈被反转,使得相同的电流流过每个线圈,但是方向相反,则互感, M 存在于tw之间o线圈将对每个线圈产生抵消效应,如下所示。
差分耦合串联电感

由线圈2的互感作用引入线圈1的电动势与线圈1中的自感电动势相反,因为现在相同的电流以相反的方向通过每个线圈。为了考虑这种抵消效应,当两个线圈的磁场差分连接时,使用负号与 M ,给出了当电感器差分时计算电路总电感的最终公式连接为:
L total = L 1 + L 2 -2M
然后,串联电感耦合电感的最终公式如下:
系列电感器No2
两个10mH的电感器分别以串联组合连接在一起,使得它们的磁场相互帮助,从而产生累积耦合。它们的互感为5mH。计算串联组合的总电感。

串联电感器示例No3
串联的两个线圈有一个自感为20mH和60mH。发现该组合的总电感为100mH。确定两个线圈之间存在的互感量,假设它们相互辅助。

串联电感中的电感
我们现在知道我们可以将串联电感连接起来产生一个总电感值, L T 等于各个值,它们加在一起,类似于串联电阻器。然而,当将电感器串联连接在一起时,它们会受到互感的影响。
相互连接的串联电感器被归类为“辅助”或“反对”总电感,这取决于线圈是否累积耦合(在
在下一个关于电感器的教程中,我们将看到线圈在并联电感器时的位置也会影响总电感,电路的L T 。
-
线圈
+关注
关注
14文章
1829浏览量
44479 -
电阻器
+关注
关注
21文章
3784浏览量
62167 -
电感器
+关注
关注
20文章
2332浏览量
70554
发布评论请先 登录
相关推荐
射频电感器的选择参数
电感器的工作原理
铁氧体环形电感器寄生电容的提取
电感器工作原理_电感的单位是什么_电感器的功能_磁环电感器用途
电感器结构的原理及电感器基础知识的分享
什么是电感器,电感器的作用是什么
什么是电感器,电感器的常见知识汇总
什么是电感器,电感器是如何工作的?
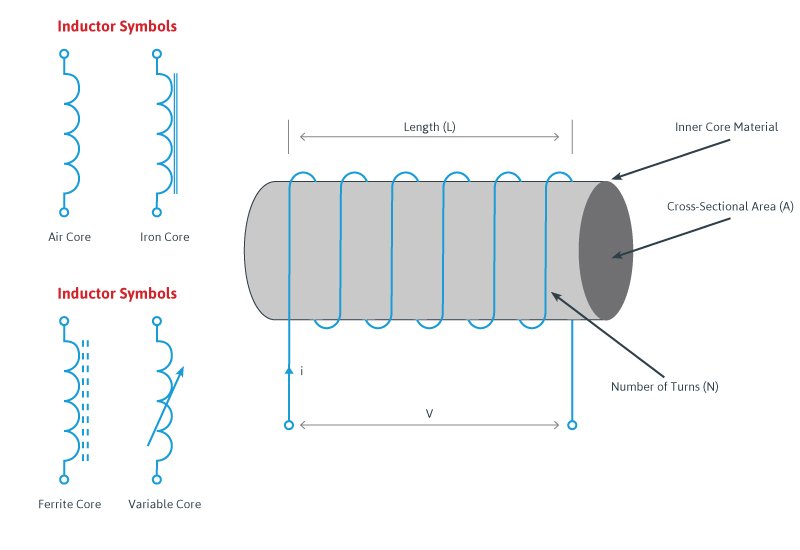




 串联电感器方程案例
串联电感器方程案例










评论