在 RC振荡器教程中,我们看到了许多电阻和电容可以通过反相放大器连接在一起产生振荡电路。
最简单的正弦波振荡器之一,它使用RC网络代替传统的LC调谐振荡电路产生正弦输出波形,称为维恩桥振荡器。
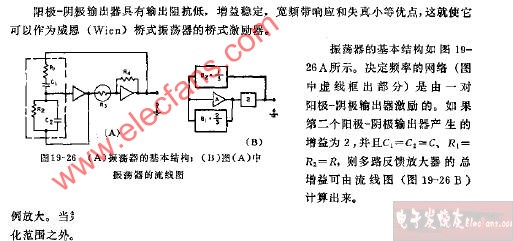
维恩桥振荡器之所以被称为是因为该电路基于惠斯通电桥电路的频率选择形式。 Wien Bridge振荡器是一个两级 RC 耦合放大器电路,在谐振频率下具有良好的稳定性,低失真并且非常容易调谐,使其成为一种流行的电路,作为音频振荡器但是相位输出信号的移位与先前的相移RC振荡器有很大不同。
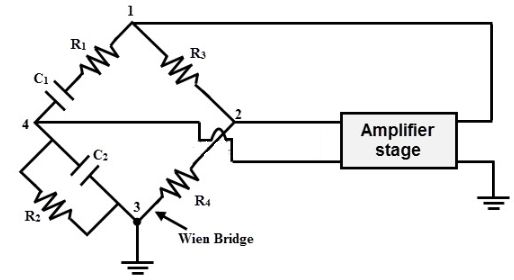
Wien Bridge Oscillator使用由一系列<组成的反馈电路 RC 电路连接相同元件值的并联 RC ,根据频率产生相位延迟或相位超前电路。在谐振频率ƒr时,相移为0 o 。考虑下面的电路。
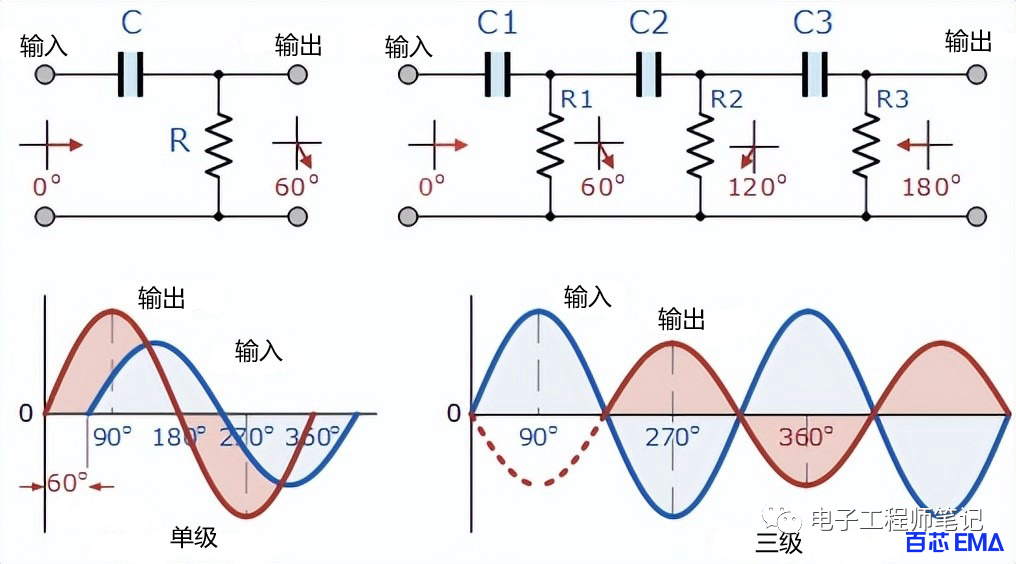
RC相移网络
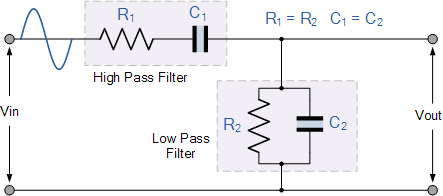
以上 RC 网络由连接到并联 RC 的串联 RC 电路组成,基本上形成连接到低通滤波器的高通滤波器,产生非常有选择性的二阶滤波器频率相关带通滤波器在所选频率ƒr时具有高 Q 因子。
在低频时串联电容的电抗( C1 )非常高,因此有点像开路,阻止 Vin 处的任何输入信号,导致几乎没有输出信号, Vout 。同样,在高频时,并联电容的电抗( C2 )变得非常低,因此这个并联电容有点像输出端的短路,所以再没有输出信号。
因此,在 C1 的两个极端之间必须有一个频率点开路, C2 在输出电压的地方短路, V OUT 达到最大值。发生这种情况的输入波形的频率值称为振荡器谐振频率,(ƒr)。
在此谐振频率下,电路电抗等于其电阻,即: Xc = R ,输入和输出之间的相位差等于零度。因此,输出电压的幅度最大,等于输入电压的三分之一(1/3)。
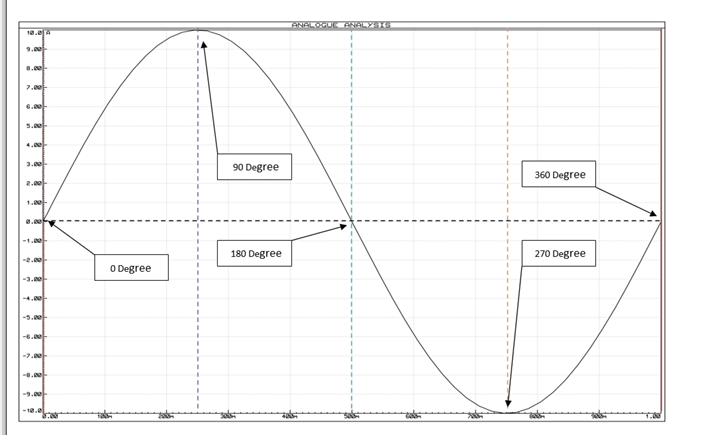
振荡器输出增益和相移
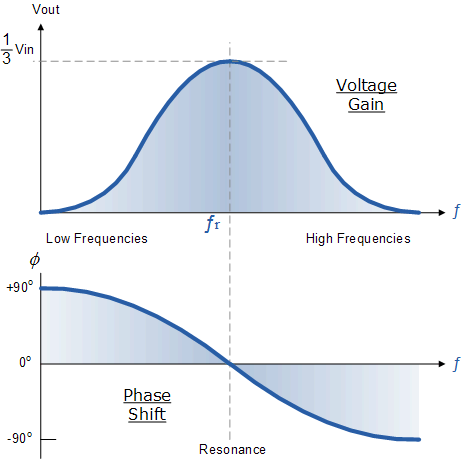
可以看出,在非常低的频率下,相位角输入和输出信号之间是“正”(相位高级),而在非常高的频率下,相位角变为“负”(相位延迟)。在这两个点的中间,电路处于其谐振频率(ƒr),两个信号是“同相”或0 o 。因此,我们可以使用以下表达式定义此共振频率点。
维恩桥振荡器频率
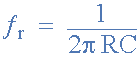
其中:
ƒr是以赫兹为单位的谐振频率
R 是以欧姆为单位的电阻
C 是法拉的电容
我们之前说过RC的输出电压幅度 Vout 网络处于其最大值并等于输入电压的三分之一(1/3), Vin 以允许发生振荡。但为什么三分之一而不是其他一些价值。为了理解为什么上述RC电路的输出需要为三分之一,即 0.333xVin ,我们必须考虑复阻抗( Z = R±jX )我们从AC理论教程中了解到,复阻抗的实部是电阻, R ,而虚部是电抗, X 。由于我们在这里处理电容,电抗部分将是容抗, Xc 。
RC网络
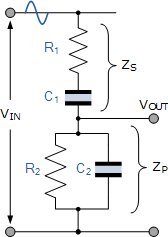
如果我们如图所示重新绘制上述RC网络,我们可以清楚地看到它由两个连接在一起的RC电路组成,其输出来自它们的结点。电阻 R 1 和电容 C 1 形成顶部串联网络,而电阻 R 2 和电容器 C 2 形成底部并联网络。
因此系列组合的总直流阻抗( R 1 C 1 )我们可以调用, Z S 和总阻抗我们可以调用并行组合( R 2 C 2 ), Z P 。当 Z S 和 Z P 在输入端有效地串联连接在一起, V IN ,它们形成一个分压器网络,输出取自 Z P ,如图所示。
让我们看看然后假设 R 1 和 R 2 的分量值相同:12kΩ,电容器 C 1 和 C 2 在以下位置相同: 3.9nF 和供电频率ƒ 3.4kHz 。
串联电路
串联组合的总阻抗电阻, R 1 和电容, C 1 只是:
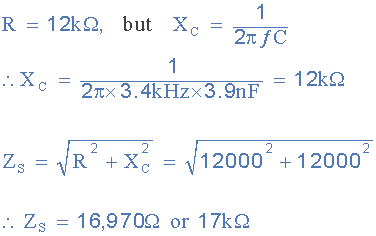
我们现在知道,电源频率为3.4kHz时,电容的电抗与电阻的电阻相同。电阻12kΩ。然后,这给出了17kΩ的上串联阻抗 Z S 。
对于较低的并联阻抗 Z P ,由于两个元件并联,我们必须区别对待,因为并联电路的阻抗受这种并联组合的影响。
并联电路
较低并联电阻的总阻抗 R 2 和电容, C 2 给出为:
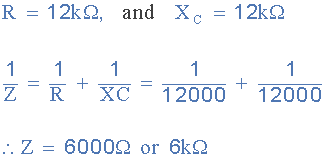
在供电频率为3400Hz或3.4kHz时,组合直流RC并联电路的阻抗变为6kΩ( R || Xc ),该并联阻抗的矢量和计算如下:
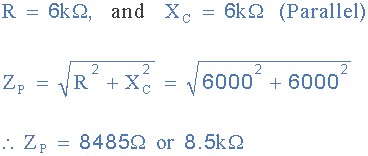
所以我们现在得到串联阻抗矢量和的值:17kΩ,(Z S =17kΩ)和并联阻抗:8.5kΩ,(Z P =8.5kΩ)。因此,给定频率下分压器网络的总输出阻抗 Zout 为:
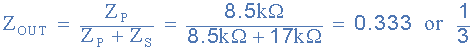
然后在振荡频率下,输出电压的幅度 Vout 将等于 ZoutxVin ,如图所示等于三分之一(1/3)输入电压 Vin ,这是频率选择 RC 网络,它构成了Wien Bridge Oscillator电路的基础。
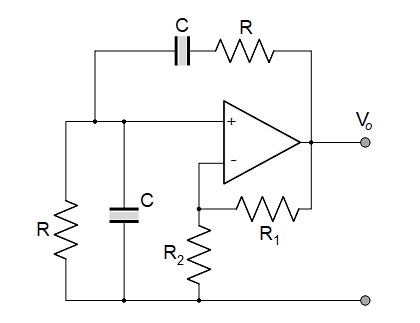
如果我们现在将此 RC 网络放置在增益为 1 + R1 / R2 的非反相放大器上,则会产生以下基本Wien桥振荡器电路。
Wien Bridge Oscillator
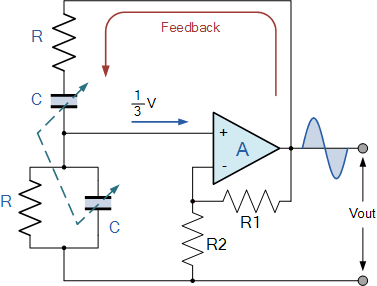
运算放大器的输出反馈给两者放大器的输入。反馈信号的一部分通过 R1 和 R2 的电阻分压器网络连接到反相输入端(负反馈或退化反馈),这允许放大器电压增益为
形成R和C的串联和并联组合的另一部分形成反馈网络,并通过反馈网络反馈到非反相输入端子(正反馈或再生反馈)。 RC Wien Bridge网络正是这种正反馈组合引起振荡。
RC网络连接在放大器的正反馈路径上,零相移一个频率。然后在选定的谐振频率(ƒr),施加到反相和非反相输入的电压将相等并且“同相”,因此正反馈将抵消负反馈信号,从而导致电路振荡。
放大器电路的电压增益必须等于或大于三个“增益= 3”才能开始振荡,因为正如我们上面所看到的,输入是1/3输出。该值(Av≥3)由反馈电阻网络 R1 和 R2 设置,对于非反相放大器,给出作为比率 1+(R1 / R2)。
此外,由于运算放大器的开环增益限制,1MHz以上的频率无法使用特殊的高电平频率运算放大器。
Wien Bridge振荡器示例No1
确定Wien Bridge Oscillator电路振荡的最大和最小频率span>10kΩ和 1nF 至 1000nF 的可变电容。
维恩桥振荡器的振荡频率如下:
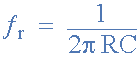
维恩桥振荡器最低频率
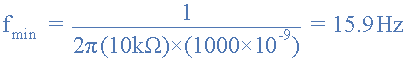
Wien Bridge Oscillator最高频率
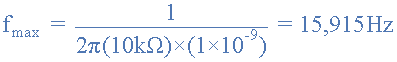
Wien桥振荡器示例No2
需要 Wien Bridge Oscillator 电路来产生5,200赫兹(5.2kHz)的正弦波形。计算频率确定电阻 R 1 和 R 2 的值,两个电容 C 1 和 C 2 以产生所需的频率。
此外,如果振荡器电路基于非反相运算放大器配置,确定增益电阻的最小值,以产生所需的振荡。最后绘制得到的振荡器电路。
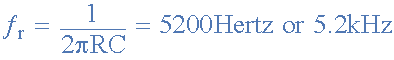
维恩桥振荡器的振荡频率为5200赫兹。如果电阻 R 1 = R 2 且电容 C 1 = C 2 我们假设反馈电容的值 3.0nF ,然后反馈电阻的对应值计算如下:
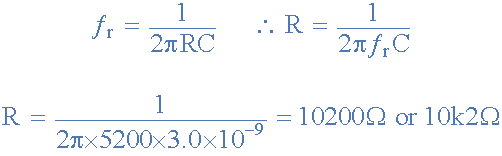
要开始正弦波振荡,维恩桥电路的电压增益必须大于或等于3,(Av≥3)。对于非反相运算放大器配置,该值由 R3 和 R4 的反馈电阻网络设置,并给出为:
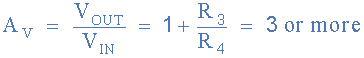
如果我们选择电阻 R3 的值,例如100kΩ的,那么电阻 R4 的值计算如下:
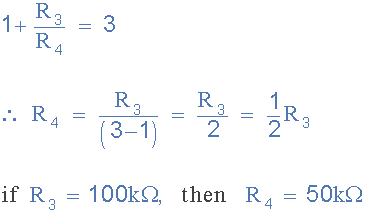
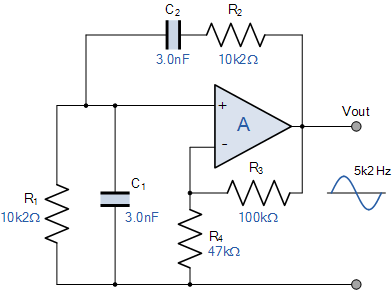
增益 3 是确保振荡所需的最小值,实际上值通常要求高一点。如果我们假设增益值3.1,则重新计算电阻 R4 ,得到47kΩ的值。这使最终的Wien Bridge振荡器电路成为:
Wien Bridge振荡器电路示例No2
Wien Bridge振荡器摘要
然后,如果在Wien Bridge Oscillator电路中发生振荡,则必须满足以下条件。
在没有输入信号的情况下,Wien Bridge振荡器会产生连续的输出振荡。
Wien Bridge振荡器可以产生大范围的频率。
放大器的电压增益必须大于3.
RC网络可与非反相放大器一起使用。
输入与 R 相比,放大器的电阻必须高,以便 RC 网络不会过载并改变所需的条件。
放大器的输出电阻必须很低,以便最大限度地减少外部负载的影响。
s的一些方法必须提供消除振荡幅度的表格。如果放大器的电压增益太小,则所需的振荡将衰减并停止。如果它太大,输出将饱和到电源轨的值并失真。
通过反馈二极管形式的振幅稳定,Wien Bridge振荡器的振荡可以无限期地继续。
在我们对振荡器的最后研究中,我们将研究使用石英晶体作为振荡电路的晶体振荡器,以产生高频且非常稳定的正弦波形。
-
电阻
+关注
关注
86文章
5507浏览量
171920 -
电路
+关注
关注
172文章
5901浏览量
172133 -
振荡器
+关注
关注
28文章
3832浏览量
139033
发布评论请先 登录
相关推荐
振荡器中的相移
一种RC振荡器一Twin-T振荡器
使用运算放大器的RC相移振荡器
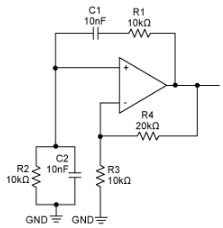
数控维恩桥振荡器的分析




 维恩桥振荡器输出增益和相移频率及案例摘要
维恩桥振荡器输出增益和相移频率及案例摘要










评论