各种不同的波形发生器

波形发生器是可以使用振荡器和脉冲电路产生正弦波，方波，三角波和锯齿波的电子电路

在之前的教程中，我们详细研究了三种不同类型的波形。基本晶体管多谐振荡器电路，可用作张弛振荡器，在其输出端产生方波或矩形波，用作时钟和定时信号。

但也可以构造基本的波形发生器来自简单集成电路或运算放大器的电路，连接到电阻 - 电容（ RC ）储能电路或石英晶体，以产生所需频率的所需二进制或方波输出波形。

如果没有数字再生开关电路的一些例子，这个波形生成教程将是不完整的，因为它说明了用于产生方波的波形发生器的开关动作和操作。用作定时或顺序波形。

我们知道，再生开关电路，如 Astable Multivibrators 是最常用的张弛振荡器类型，因为它们产生恒定的方波输出，使得它们非常适合用作数字在之前的教程中，我们详细研究了三种不同类型的波形。基本晶体管多谐振荡器电路，可用作张弛振荡器，在其输出端产生方波或矩形波，用作时钟和定时信号。

但也可以构造基本的波形发生器来自简单集成电路或运算放大器的电路，连接到电阻 - 电容（ RC ）储能电路或石英晶体，以产生所需频率的所需二进制或方波输出波形。

Astable多谐振荡器可以产生出色的振荡器，因为它们以恒定的重复频率在两个不稳定状态之间连续切换，从而产生连续的方波输出从输出开始，1：1标记 - 空间比（“ON”和“OFF”相同），在本教程中，我们将看到一些不同的方法，我们可以使用标准TTL和CMOS逻辑电路以及一些额外的离散时序组件。

施密特波形发生器

简单的波形发生器可以使用基本的施密特触发器动作逆变器构建，例如TTL 74LS14。到目前为止，这种方法是制作基本的非稳态波形发生器的最简单方法。当用于产生时钟或定时信号时，非稳态多谐振荡器必须产生稳定的波形，在“高”和“低”状态之间快速切换，没有任何失真或噪声，施密特反相器就是这样做的。

我们知道施密特反相器的输出状态与其输入状态（非门原理）的输出状态相反或相反，并且它可以在不同的电压电平下改变状态，从而使其具有“滞后”。

施密特反相器使用施密特触发器动作，当输入电压信号在输入端子周围增加和减小时，该操作在上阈值电平和下阈值电平之间改变状态。该上阈值电平“设置”输出，下阈值电平“复位”输出，其分别等于逆变器的逻辑“0”和逻辑“1”。考虑下面的电路。

施密特反相器波形发生器

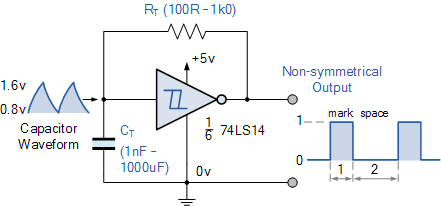
这个简单的波形发生器电路由一个TTL 74LS14施密特反相器逻辑门组成，其一个电容器， C 连接在其输入端和地之间，（0v）和电路振荡所需的正反馈由反馈电阻提供， R 。

那么它是如何运作的？假设电容器板上的电荷低于施密特的0.8伏特下限阈值（数据表值）。因此，这使得逆变器的输入处于逻辑“0”电平，从而产生逻辑“1”输出电平（逆变器原理）。

电阻器 R 的一侧是现在连接到逻辑“1”电平（+ 5V）输出，而电阻器的另一端连接到电容器， C 处于逻辑“0”电平（0.8v或更低） 。电容器现在开始通过电阻器以正方向充电，其速率由组合的 RC 时间常数决定。

当电容器两端的电荷达到1.6时施密特触发器的电压上限阈值（数据表值）施密特反相器的输出迅速从逻辑电平“1”变为逻辑电平“0”状态，并且流过电阻器的电流改变方向。

此变化现在导致最初通过电阻器充电的电容器 R 开始通过同一电阻器自身放电，直到电容器板上的电荷达到0.8的下限阈值电平电压和逆变器输出再次切换状态，只要电源电压存在，循环就会一遍又一遍地重复。

因此电容器 C 不断充电和放电在施密特逆变器的输入上阈值电平和下阈值电平之间的每个周期期间，其自身在逆变器输出处产生逻辑电平“1”或逻辑电平“0”。然而，由于TTL的输入栅极特性，输出波形不对称，产生约33％或1/3的占空比，因为“HIGH”和“LOW”之间的标记 - 空间比分别为1：2。

反馈电阻的值（ R ）也必须保持低至1kΩ以使电路正确振荡，220R至470R是好的，通过改变电容器的值， C 来改变频率。同样在高频电平时，输出波形从方形波形变为梯形波形，因为TTL栅极的输入特性受到电容器的快速充电和放电的影响。因此，施密特波形发生器的振荡频率如下：

施密特波形频率

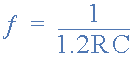
电阻值介于： 100R至1kΩ之间，电容值介于： 1nF至1000uF 之间。这将产生1Hz至1MHz的频率范围（高频产生波形失真）。

通常，标准TTL逻辑门由于其平均输入和输出特性而不能像波形发生器那样工作得很好，输出波形失真，所需反馈电阻值低，导致低频运行时产生较大的高值电容。

如果反馈电容的值太小，TTL振荡器也不会振荡。然而，我们还可以使用更好的CMOS逻辑技术制造Astable多谐振荡器，该技术采用3V至15V电源供电，例如CMOS 40106B施密特反相器。

CMOS 40106是具有相同施密特触发器的单输入反相器作为TTL 74LS14，但具有非常好的抗噪性，高带宽，高增益和出色的输入/输出特性，可产生更“平方”的输出波形，如下所示。

CMOS施密特波形发生器

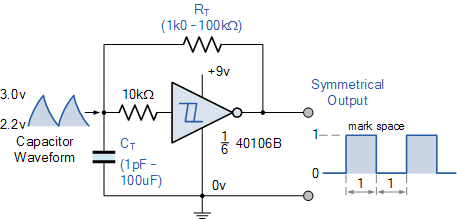
用于CMOS 40106的施密特波形发生器电路基本上与之前的TTL 74LS14逆变器相同，除了增加了10kΩ电阻，用于防止电容器损坏敏感MOSFET输入晶体管，因为它在较高频率下快速放电。

标记 - 空间比率更均匀大约1：1匹配，反馈电阻值增加到100kΩ以下，导致更小和更小r定时电容， C 。振荡频率可能与:( 1 / 1.2RC ）不同，因为CMOS输入特性与TTL不同。电阻值介于：1kΩ和100kΩ之间，电容值介于： 1pF至100uF 之间。这将提供0.1Hz至100kHz之间的频率范围。

施密特反相器波形发生器也可以由连接的各种不同逻辑门构成逆变器电路。基本的施密特非稳态多谐振荡器电路可以通过一些额外的元件轻松修改，以产生不同的输出或频率。例如，两个反向波形或多个频率，通过将固定反馈电阻更改为电位计，输出频率可以如下所示变化。

时钟波形发生器

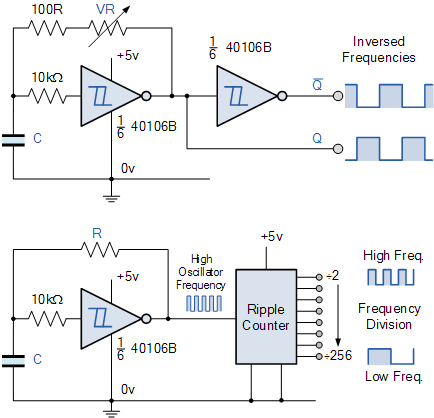
在上面的第一个电路中，施密特波形发生器的输出中添加了一个额外的施密特反相器，以产生第二个波形，即反向或镜像第一个产生两个互补输出波形的图像，所以当一个输出为“高”时，另一个输出为“低”。第二个施密特反相器也改善了反向输出波形的形状，但增加了一个小的“门延迟”，因此它与第一个不完全同步。

此外，振荡器电路的输出频率可以通过将固定电阻 R 更改为电位计来改变，但仍需要一个较小的反馈电阻，以防止电位器在其最小值0Ω时将输出短路。 SPAN>。

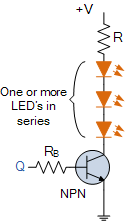
我们也可以使用第一个电路的两个互补输出 Q 和 Q 来交替使用如图所示，通过将它们的输出直接连接到两个开关晶体管的基极来闪烁两组灯或LED。

这样，一个或多个LED与开关晶体管的集电极串联连接在一起，导致交替当每个晶体管依次切换为“ON”时，每组LED闪烁。

使用这种类型的电路时，记得计算一个合适的串联电阻， R 来限制对于您正在使用的电压，LED电流低于20mA（红色LED）。

为了产生几赫兹的极低频输出以闪烁LED，施密特波形发生器使用高值定时电容器

一种替代解决方案是使用较小值的电容器来产生更高的频率，比如说1kHz或10kHz，然后将此主时钟频率分频为单个较小的频率，直到达到所需的低频值，上面的第二个电路就是这样。

上面的下面的电路显示正在使用的振荡器驱动纹波计数器的时钟输入。纹波计数器基本上是多个2分频，D型触发器级联在一起形成单个N分频计数器，其中N等于计数器位计数，如CMOS 4024 7位纹波计数器或CMOS 4040 12位纹波计数器。

施密特非稳态时钟脉冲电路产生的固定时钟频率分为多个不同的子频率，如ƒ÷2 ，ƒ÷4，ƒ÷8，ƒ÷256 等，直到所使用的纹波计数器的最大“除以n”值。使用“触发器”，“二进制计数器”或“纹波计数器”将主固定时钟频率划分为不同的子频率的过程称为频率分割，我们可以使用它来从中获取多个频率值。单个波形发生器。

NAND门波形发生器

施密特波形发生器也可以使用连接的标准CMOS逻辑NAND门来产生逆变器电路。这里，两个 NAND 门连接在一起，产生另一种 RC 张弛振荡器电路，它将产生如下所示的方波形输出波形。

NAND门波形发生器

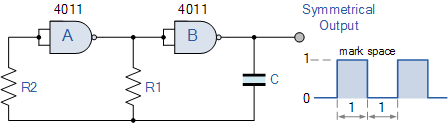
在这种波形发生器电路中， RC 网络由电阻器 R1 和电容器 C 组成，此 RC 网络由第一个 NAND的输出控制门。此 R1C 网络的输出通过电阻器 R2 反馈到第一个 NAND 门的输入端，当电容器两端的充电电压反馈时达到第一个 NAND 门的上限阈值， NAND 门改变状态，导致第二个 NAND 门跟随它，从而改变状态和产生输出电平的变化。

R1C 网络上的电压现在反转，电容开始通过电阻放电，直到达到第一个电压的下阈值电平。 NAND 门使两个门再次改变状态。与上面的上述施密特波形发生器电路一样，振荡频率由 R1C 时间常数决定，时间常数为： 1 / 2.2R1C 。通常 R2 的值为电阻 R1 的10倍。

当需要高稳定性或保证自启动时，CMOS波形发生器可以使用三个反相 NAND 门或任何三个逻辑逆变器来制作，如下所示连接在一起产生一个有时被称为“三环”的电路波形发生器。振荡频率由 R1C 时间常数再次确定，与上面的两个门振荡器相同，并且当 1 / 2.2R1C > R2 的值是电阻值的10倍， R1 。

稳定的NAND门波形发生器

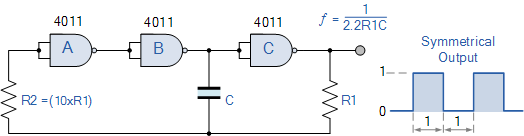
增加额外的 NAND 门可确保即使电容值非常低，振荡器也会启动。此外，波形发生器的稳定性得到极大改善，因为它的阈值触发电平几乎是电源电压的一半，因此不易受电源变化的影响。

稳定量主要取决于振荡频率，一般来说，频率越低，振荡器越稳定。

这种波形发生器的工作量接近一半或50％在电源电压中，所得到的输出波形具有非常接近50％的占空比，1：1的标记空间比。三栅极波形发生器比上述两个栅极振荡器具有许多优点，但其一大缺点是它使用额外的逻辑门。

环型波形发生器

我们已经看到以上波形发生器可以使用TTL和更好的CMOS逻辑技术制造，其中 RC 网络在连接一个，两个或偶数时在电路内产生时间延迟三个逻辑门形成一个简单的RC弛豫振荡器。但是我们也可以使用Logic NOT Gates或换句话说 Inverters 来制作波形发生器，而不需要连接任何其他无源元件。

通过将任何ODD连接在一起

b> NOT 门的编号（3,5,7,9等）形成“环”电路，使环的输出直接连接到电路环的输入端当逻辑电平“1”不断围绕网络旋转时，将继续振荡，产生的输出频率由所使用的逆变器的传播延迟决定。

环形波形发生器

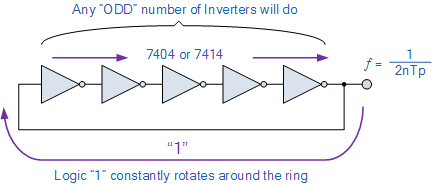
振荡频率取决于所使用的 Inverters 的总传播延迟在环内并且其本身由栅极技术的类型决定，即逆变器的TTL，CMOS，BiCMOS。传播延迟或传播时间是信号从到达输入端的逻辑“0”直接通过逆变器所需的总时间（通常以纳秒为单位），产生逻辑“1”

对于这种类型的环形波形发生器电路，电源电压，温度和负载电容的变化都会影响逻辑门的传播延迟。通常，平均传播延迟时间将在制造商数据表中给出，使用的数字逻辑门类型的振荡频率如下：

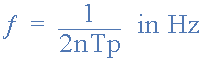
其中：ƒ是振荡频率， n 是使用的门数， Tp 是每个门的传播延迟。

例如，假设一个简单的波形发生器电路有5个单独的逆变器串联连接在一起形成环振荡器，每个逆变器的传播延迟以 8ns 给出。那么振荡的频率将给出如下：

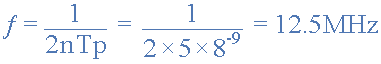
当然，这实际上并不是一个实际的振荡器它的不稳定性和非常高的振荡频率，10兆赫兹取决于所使用的逻辑门技术的类型，在我们的简单例子中它被计算为12.5MHz !!通过改变环内使用的 Inverters 的数量，可以稍微“调整”环形振荡器输出频率，但使用更稳定的 RC 波形发生器要好得多我们在上面讨论过的。

然而，它确实表明逻辑门可以连接在一起产生基于逻辑的波形发生器和设计糟糕的数字电路，有许多门，信号路径和反馈回路已知无意间振荡。

通过逆变器电路上的 RC 网络，可以精确控制振荡频率，从而产生更实用的非稳态振荡振荡器用于许多通用电子应用的电路。