材料的电阻率是对电流流动的阻力,某些材料比其他材料更能抵抗电流流动
欧姆法律规定当电压(V)源之间施加电压时在这两个点之间存在电位差的情况下,电路中的两个点,电流(I)将在它们之间流动。流动的电流量受到存在的电阻(R)的限制。换句话说,电压会促使电流流动(电荷的移动),但阻力却是阻力。
我们总是用欧姆测量电阻,其中欧姆用希腊字母Omega表示,Ω。例如:50Ω,10kΩ或4.7MΩ等。导体(例如电线和电缆)通常具有非常低的电阻值(小于0.1Ω),因此我们可以忽略它们,因为我们在电路分析计算中假设电线为零抵抗性。另一方面,绝缘体(例如塑料或空气)通常具有非常高的电阻值(大于50MΩ),因此我们也可以忽略它们用于电路分析,因为它们的值太高。
但电气两点之间的电阻可取决于许多因素,例如导体长度,其横截面积,温度以及制造它的实际材料。例如,假设我们有一根长度 L 的导线(导体),横截面积 A 和电阻 R 如图所示。
单导体

电阻,R这个简单的导体是其长度L和导体面积的函数.A欧姆定律告诉我们,对于给定的电阻R,流过导体的电流与施加的电压成比例,即I = V / R.现在假设我们将两个相同的导体以串联组合连接在一起,如图所示。
导体长度加倍
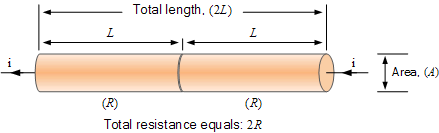
这里通过串联组合将两根导线连接在一起,即端到端,我们有效地将导体的总长度加倍(2L),而横截面积A仍然是和之前一样。但是,除了长度加倍之外,我们还将导体的总电阻加倍,得到2R为:1R + 1R = 2R。
因此我们可以看到导体的电阻与其成正比长度,即:RαL。换句话说,我们预计导体(或导线)的电阻会随着导体(或导线)的长时间成比例地增大。
还要注意,导体的长度和导体的电阻加倍(2R) ,为了强制相同的电流, i 像以前一样流过导体,我们需要加倍(增加)施加的电压,因为现在I =(2V)/(2R)。接下来假设我们将两个相同的导体并联组合在一起,如图所示。
将导体面积加倍
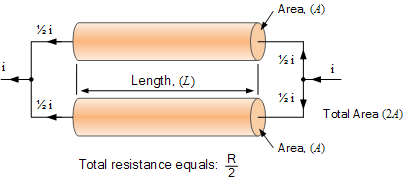
这里通过并联组合将两个导体连接在一起,我们有效地将总面积增加了一倍,而导体长度L保持与原始单导体相同。但是,除了将面积加倍之外,通过将两个导体并联连接在一起,我们有效地将导体的总电阻减半,得到1 / 2R,因为现在每一半的电流都流过每个导体支路。
因此,导体的电阻与其面积成反比,即:R1 /αA或Rα1/ A.换句话说,我们期望导体(或导线)的电阻成比例地越小,其横截面积就越大。
同样通过将面积加倍并因此使总电阻减半。导体分支(1 / 2R),对于相同的电流, i 流过并联导体支路,如前所述我们只需要一半(减小)所施加的电压,因为现在I =(1 / 2V)/ (1 / 2R)。
所以希望我们可以看到导体的电阻与导体的长度(L)成正比,即:RαL,与其面积(A),Rα1/ A成反比。因此,我们可以正确地说抵抗是:
抵抗的比例
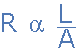
但是除了长度和导体面积之外,我们还期望导体的电阻取决于制造它的实际材料,因为不同的导电材料,铜,银,铝等都具有不同的物理和电学性质。因此,我们可以简单地通过在上面的等式中加上“比例常数”将上述等式的比例符号(α)转换为等号,给出:
电阻率方程

式中:R是以欧姆为单位的电阻(Ω),L是以米(m)为单位的长度,A是以平方米为单位的面积(m 2 ),其中比例常数ρ(希腊字母“rho”)被称为电阻率。
电阻率
特定导体材料的电阻率是材料抵抗通过它的电流强度的量度。该电阻率因子,有时称为“特定电阻”,使得不同类型导体的电阻能够根据它们的物理特性在特定温度下相互比较,而不考虑它们的长度或横截面积。因此,ρ的电阻率值越高,电阻越大,反之亦然。
例如,铜等导体的电阻率约为1.72 x 10 -8 欧姆表(或17.2nΩm),而空气等不良导体(绝缘体)的电阻率可以超过1.5 x 10 14 或150万亿Ωm。
材料例如铜和铝因其低电阻率而闻名,因此允许电流容易地流过它们,使得这些材料成为制造电线和电缆的理想选择。银和金的电阻率值很低,但由于显而易见的原因,变成电线的成本更高。
那么影响导体电阻(R)的因素可以列为: / p>
制造导体的材料的电阻率(ρ)。
总长度( L)导体。
导体的横截面积(A)。
导体的温度。
电阻率示例No1
如果铜的电阻率为20 <,则计算100米2.5mm 2 铜线的总直流电阻sup> o C为1.72 x 10 -8 Ω米。
给出的数据:20 o C时铜的电阻率为1.72 x 10 -8 ,线圈长度L = 100m,导体的横截面积为2.5mm 2 ,其面积为:A = 2.5×10 -6 米 2 。
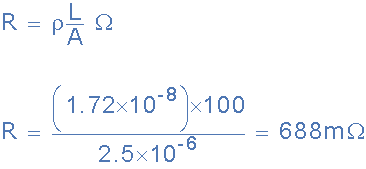
那是688毫米i-ohms或0.688欧姆。
我们之前说过,电阻率是每单位长度和每单位导体横截面积的电阻,因此表明电阻率ρ具有欧姆表的尺寸,或Ωm因为它是通常写的。因此,对于特定温度下的特定材料,其电阻率为:
电阻率,Rho

电气电导率
虽然电阻(R)和电阻率(或电阻率)ρ都是所用材料的物理性质,以及其长度表示的物理形状和尺寸的函数( L)及其截面积(A),导电率或比电导与电流流过材料的容易程度有关。
电导(G)是电阻的倒数(1 / R),电导单位是西门子(S),并给出倒置欧姆符号mho,℧。因此,当导体具有1西门子(1S)的电导时,其电阻为1欧姆(1Ω)。因此,如果其电阻加倍,则电导减半,反之亦然:西门子= 1 /欧姆,或欧姆= 1 /西门子。
虽然导体电阻给出了它对电阻的影响。在电流流动中,导体的电导表明它允许电流流动的容易程度。因此,铜,铝或银等金属具有非常大的电导值,这意味着它们是良导体。
电导率σ(希腊字母sigma)是电阻率的倒数。即1 /ρ,以西门子每米(S / m)为单位进行测量。由于电导率σ= 1 /ρ,前面的电阻表达式R可以改写为:
作为电导率函数的电阻
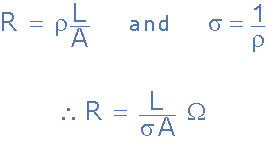
然后我们可以说电导率是导体通过没有电阻损耗的电流或信号的效率。因此,具有高导电率的材料或导体将具有低电阻率,反之亦然,因为1西门子(S)等于1Ω -1 。因此铜是一种良好的电流导体,其导电率为每米58.14 x 10 6 西门子。
电阻率实例No2
20米电缆长度的横截面积为1mm 2 ,电阻为5欧姆。计算电缆的电导率。
给出的数据:直流电阻,R = 5欧姆,电缆长度,L = 20m,导体的横截面积为1mm 2 给出面积:A = 1 x 10 -6 米 2 。
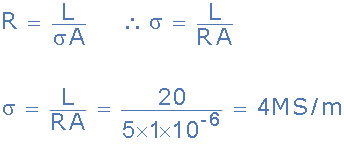
这是每米长度为4兆西门子。
电阻率概述
我们在本教程中已经看到电阻率,电阻率是属性的材料或导体,指示材料传导电流的程度。我们还看到,导体的电阻(R)不仅取决于制造导体的材料,铜,银,铝等,还取决于其物理尺寸。
导体的电阻与其长度(L)成正比,如RαL。因此,它的长度加倍会使其阻力加倍,而将其长度减半会使其阻力减半。此外,导体的电阻与其横截面积(A)成反比,如Rα1/ A.因此,将其横截面积加倍会使其阻力减半,而将其横截面积减半会使其阻力加倍。
我们还了解到导体(或材料)的电阻率(符号:ρ)与制造它的物理性质有关,并且因材料而异。例如,铜的电阻率通常为:1.72×10 -8 Ωm。特定材料的电阻率以欧姆 - 米(Ωm)为单位测量,也受温度的影响。
根据特定材料的电阻率值,它可以归类为“导体”,“绝缘体”或“半导体”。请注意,半导体是其导电性取决于添加到材料中的杂质的材料。
电阻率在配电系统中也很重要,因为接地系统对电力和配电系统的有效性很大程度上取决于关于系统地面位置的土壤和土壤材料的电阻率。
传导是以电流形式给予自由电子运动的名称。电导率,σ是电阻率的倒数。即1 /ρ,单位为西门子每米,S / m。电导率范围从零(对于完美的绝缘体)到无穷大(对于完美的导体)。因此,超导体具有无限电导和几乎零欧姆电阻。
-
电阻
+关注
关注
86文章
5515浏览量
172045 -
电流
+关注
关注
40文章
6863浏览量
132198 -
电导率
+关注
关注
1文章
205浏览量
13925
发布评论请先 登录
相关推荐
电阻率对电路性能的影响分析
霍尔电流检测芯片检测多大电流
电阻阻隔的是电压还是电流,电阻阻挡的电流会流失吗
逆变器绝缘抵抗和残余电流不同,发生较大故障

导体的电阻大小和导体的什么成正比
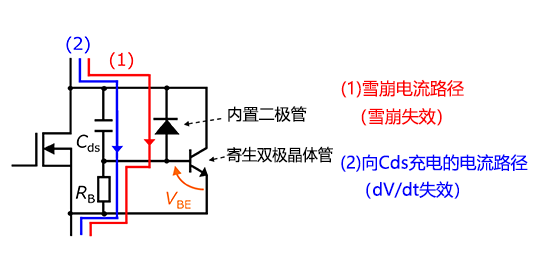
什么是雪崩击穿 雪崩失效电流路径示意图
浅谈剩余电流动作保护器在接地系统中的应用




 导体抵抗电流流动力及比例方程案例概述
导体抵抗电流流动力及比例方程案例概述










评论