并联谐振发生在供电频率在电源电压和电流之间产生零相位差时产生电阻电路
在许多方面,并联谐振电路正是如此与我们在前一个教程中看到的串联谐振电路相同。两者都是3元件网络,包含两个无功元件,使它们成为二阶电路,两者都受到电源频率变化的影响,两者都有一个频率点,它们的两个电抗元件相互抵消,影响电路的特性。两个电路都有一个谐振频率点。
然而,这次的不同之处在于,并联谐振电路受到并联LC谐振电路中流过每个并联支路的电流的影响。储能电路是 L 和 C 的并联组合,用于滤波器网络中以选择或拒绝AC频率。考虑下面的并行RLC电路。
并行RLC电路
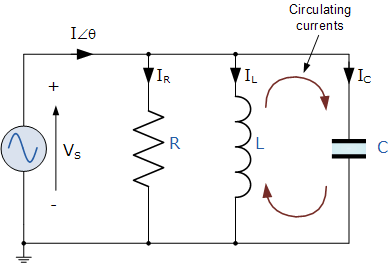
让我们定义一下我们已经知道了并联RLC电路。

一个包含电阻, R ,电感的并联电路,<当通过并联组合的合成电流同相时,span> L 和电容 C 将产生并联谐振(也称为反谐振)电路与供电电压。在谐振时,由于振荡的能量,电感和电容之间会有大的循环电流,然后并联电路产生电流谐振。
并联谐振电路存储电感器的磁场中的电路能量和电容器的电场。这种能量不断地在电感和电容之间来回传递,从而导致从电源汲取零电流和能量。
这是因为 I 的相应瞬时值L 和 I C 总是相等且相反,因此从电源汲取的电流是这两个电流的矢量加法和电流在 I R
在交流并联谐振电路的解决方案中,我们知道电源电压对所有分支都是通用的,所以这可以被视为我们的参考载体。每个并联支路必须像串联电路一样单独处理,以便并联电路的总供电电流是各个支路电流的矢量加法。
然后我们有两种方法可用于分析并联谐振电路。我们可以计算每个分支中的电流然后加在一起或计算每个分支的导纳以找到总电流。
我们从前面的串联谐振教程中知道,当 V <时,会发生谐振sub> L = -V C 当两个电抗相等时发生这种情况, X L = X ç 。并联电路的导纳如下:
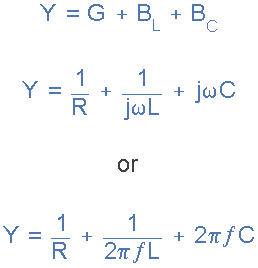
当 X L时发生共振 = X C , Y 的虚部变为零。然后:
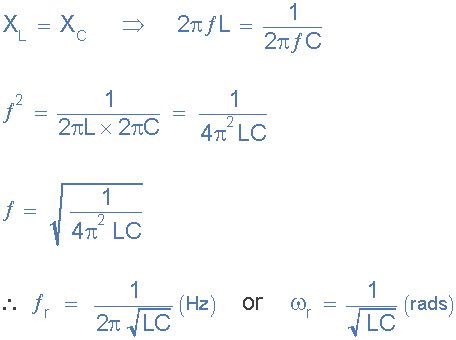
请注意,在谐振时,并联电路产生与串联谐振电路相同的等式。因此,如果电感器或电容器并联或串联连接没有区别。
同样在谐振时,并联的 LC 槽路电路就像开路一样,电路电流为仅由电阻确定, R 。因此谐振时并联谐振电路的总阻抗变为电路中电阻的值,如图所示 Z = R 。
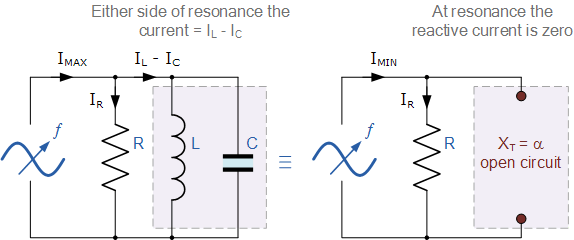
因此,在谐振时,并联电路的阻抗处于其最大值并且等于电路的电阻,从而产生高电阻和低电流的电路条件。同样在谐振时,由于电路的阻抗现在仅为电阻,因此总电路电流 I 将与电源电压“同相”, V S 。
我们可以通过改变电阻值来改变电路的频率响应。如果 L 和 C 保持不变,则更改 R 的值会影响在谐振时流过电路的电流量。然后,谐振电阻 Z = R MAX 的电路阻抗称为电路的“动态阻抗”。
并联谐振电路中的阻抗
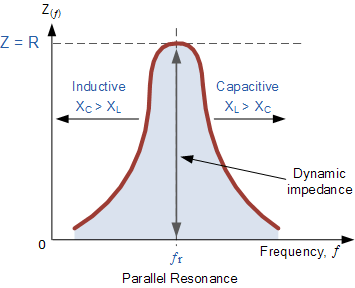
注意,如果并联电路的阻抗在谐振时最大,那么电路导纳必须处于最小值,并联谐振电路的一个特性是导纳非常低,限制了电路电流。与串联谐振电路不同,并联谐振电路中的电阻对电路带宽具有阻尼作用,使电路选择性较差。
此外,由于电路电流对于任何阻抗值都是恒定的, Z ,并联谐振电路两端的电压与总阻抗的形状相同,对于并联电路,电压波形通常取自电容器。
我们现在知道了在谐振频率下,ƒ r 电路的导纳处于最小值,等于给出的电导 G 1 / R 因为在并联谐振电路中,导纳的虚部,即电纳, B 为零,因为 B L = B C ,如图所示。
共振时的接受
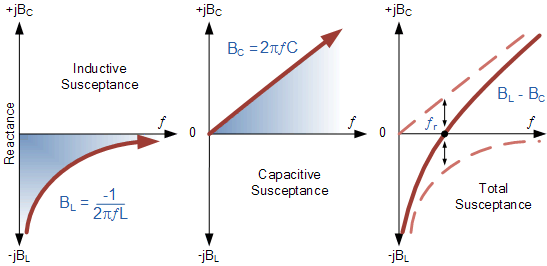
从上面看,感应电纳, B L 与f成反比以双曲线表示的频率。 电容电纳, B C 与频率成正比,因此用直线表示。最后的曲线显示了并联谐振电路的总电纳与频率的关系曲线,并且是两个电纳的差值。
然后我们可以看到在谐振频率点它是否穿过水平轴总电路电纳为零。低于谐振频率点,感应电纳主导电路产生“滞后”功率因数,而高于谐振频率点,容性电纳主导产生“超前”功率因数。
因此在谐振频率,ƒr从电源汲取的电流必须与施加的电压“同相”,因为并联电路中只有电阻,因此功率因数变为1或1(θ= 0 o )。
同样随着并联电路的阻抗随频率变化,这使得电路阻抗随着电流的变化而“动态”谐振与电压同相,因为电路的阻抗充当电阻。然后我们已经看到谐振时并联电路的阻抗等于电阻值,因此该值必须代表最大动态阻抗( Z d )如图所示的电路。
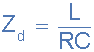
并联谐振电路中的电流
由于谐振频率下的总电纳为零,导纳处于最小值并且是等于电导, G 。因此,在谐振时,流过电路的电流也必须处于最小值,因为电感和电容支路电流相等( I L = I C )并且180° o 异相。
我们记得在并联RLC电路中流动的总电流等于各个支路电流的矢量和给定频率计算如下:
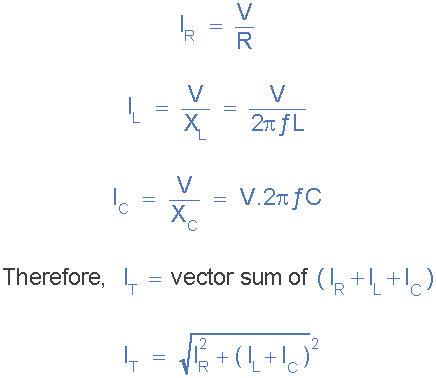
在共振时,电流 I L 和 I C 相等并取消,给出的无功电流等于零。然后在共振时,上面的等式变为。
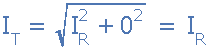
由于流经并联谐振电路的电流是电压除以阻抗,在谐振时,阻抗 Z 处于其最大值,( = R )。因此,该频率下的电路电流将处于其最小值 V / R ,并联谐振电路的电流与频率的关系曲线如下所示。
并联电路共振电流
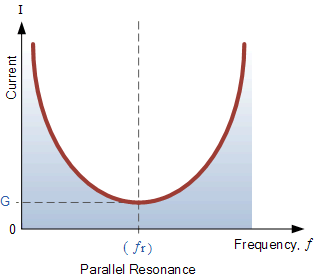
并联谐振电路的频率响应曲线表明电流的大小是频率函数并将其绘制到图表上,向我们显示当 I MIN = I R 然后再次增加到最大值,因为ƒ变为无限。
这样做的结果是流过电感器的电流幅度 L 和电容器 C 槽电路可以变得比电源电流大许多倍即使在共振时,但由于它们是相等的并且相反(180 o 异相),它们有效地相互抵消。
由于并联谐振电路仅起作用在这种类型的电路中,这种类型的电路也称为“抑制电路”,因为在谐振时,电路的阻抗处于最大值,从而抑制或抑制频率等于其谐振频率的电流。并联电路中谐振的影响也称为“电流谐振”。
上面用于定义并联谐振电路的计算和曲线图类似于我们用于串联电路的那些。然而,并联电路的特性和曲线图与串联电路的特性和曲线图完全相反,并联电路的最大和最小阻抗,电流和放大倍数相反。这就是并联谐振电路也被称为反谐振电路的原因。
带宽&amp;并联谐振电路的选择性
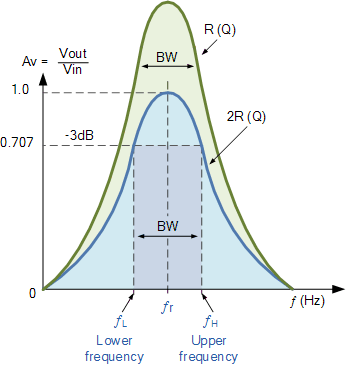
并联谐振电路的带宽定义方式与串联谐振电路完全相同。上限和下限截止频率分别为:ƒ上 和ƒ下 分别表示半功率电路中功耗消耗的频率是谐振频率 0.5(I 2 R)时消耗的全功率的一半,这给出了相同的-3dB点电流值等于其最大谐振值的70.7%,(0.707 x I) 2 R
与串联电路一样,如果谐振频率保持不变,品质因数增加,Q将导致带宽减少,同样,品质因数的降低将导致带宽增加,如下所定义:
BW =ƒ r / Q 或 BW =ƒ upper - ƒ lower
同时改变电感, L 和电容之间的比率, C 或电阻值 R 带宽,因此f对于固定的谐振频率,电路的频率响应将改变。该技术广泛用于无线电和电视发射机和接收机的调谐电路。
并联谐振电路的选择性或Q因子通常定义为循环的比率分支电流到电源电流并给出如下:

注意并联谐振的Q因子电路是串联电路Q因子表达式的倒数。同样在串联谐振电路中,Q因子给出了电路的电压放大倍数,而在并联电路中它给出了电流放大率。
并联谐振电路的带宽
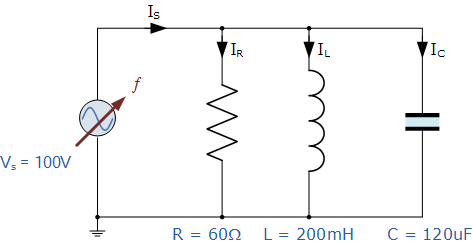
并联谐振示例No1
并联谐振网络由一个60Ω的电阻,一个120uF的电容和一个200mH的电感组成,连接在正弦电源上在所有频率下具有100伏特恒定输出的电压。计算电路的谐振频率,品质因数和带宽,谐振电路电流和电流放大倍数。
1。谐振频率,ƒ r

2。共振时的感应电抗, X L
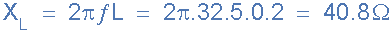
3。品质因数, Q
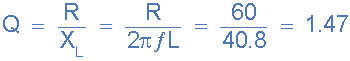
4。带宽, BW
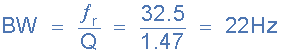
5。上下-3dB频率点,ƒ H 和ƒ L
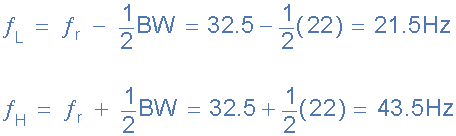
6。谐振时的电路电流, I T
谐振时,电路的动态阻抗等于 R
7。当前放大倍数, I mag
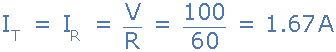
请注意从供应处获取的电流谐振(电阻电流)仅为1.67安培,而流过 LC 振荡电路的电流在2.45安培时更大。我们可以通过计算在谐振时流过电感(或电容)的电流来检查该值。
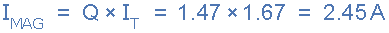
并行谐振教程摘要
我们已经看到并联谐振电路类似于串联谐振电路。当总电路电流与电源电压“同相”时,谐振发生在并联RLC电路中,因为两个无功分量相互抵消。
谐振时,电路的导纳处于最小值并且等于电路的电导。同样在谐振时,从电源汲取的电流也是最小的,并由并联电阻的值决定。
用于计算谐振频率点的公式对于前一个串联电路是相同的。然而,虽然在串联RLC电路中使用纯或不纯的元件不会影响谐振频率的计算,但在并联RLC电路中却是如此。
在本教程中关于并联谐振,我们假设两个无功分量是纯电感和纯电容,零阻抗。然而实际上,电感器将包含一些串联电阻, R S 及其感应线圈,因为电感器(和螺线管)是缠绕的线圈,通常由因此,上面用于计算纯并联谐振电路的并联谐振频率ƒ r 的基本公式将会出现在中央磁芯上。
需要稍微修改以考虑具有串联电阻的不纯电感。
使用不纯电感的谐振频率
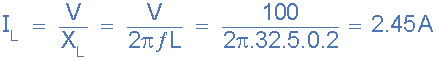
其中:L是线圈的电感,C是并联电容,R S 是线圈的直流电阻值。
-
并联
+关注
关注
5文章
242浏览量
35571 -
频率
+关注
关注
4文章
1536浏览量
59431 -
谐振电路
+关注
关注
11文章
165浏览量
27053 -
曲线
+关注
关注
1文章
82浏览量
20919
发布评论请先 登录
相关推荐




 并联谐振电路频率阻抗及计算曲线带宽案例摘要
并联谐振电路频率阻抗及计算曲线带宽案例摘要










评论