二阶(或两极)滤波器由两个连接在一起的RC滤波器部分组成,提供-40dB /十倍的滚降速率
二阶滤波器也被称为VCVS滤波器,因为运算放大器用作压控电压源放大器,是另一种重要类型的有源滤波器设计,因为我们先前看过的有源一阶RC滤波器,高阶滤波器可以使用它们设计电路。
在这个模拟滤波器部分的教程中,我们研究了无源滤波器和有源滤波器设计,并且已经看到一阶滤波器可以通过使用额外的滤波器轻松转换为二阶滤波器输入或反馈路径中的 RC 网络。然后我们可以将二阶滤波器简单地定义为:“两个一阶滤波器与放大级联在一起”。
二阶滤波器的大多数设计通常以其发明者命名,最常见的滤波器类型为: Butterworth , Chebyshev , Bessel 和 Sallen-Key 。所有这些类型的滤波器设计均可用作:低通滤波器,高通滤波器,带通滤波器和带阻(陷波)滤波器配置,以及二阶滤波器,均具有每分钟40dB的滚降。
Sallen-Key滤波器设计是最广为人知和最受欢迎的二阶滤波器设计之一,只需要一个运算放大器用于增益控制,四个无源RC滤波器就可以完成调谐。
大多数有源滤波器仅由运算放大器,电阻器和电容器组成,其截止点通过反馈实现,无需在无源一阶滤波器电路中使用电感器。
二阶(两极)有源滤波器,无论是低通还是高通,在电子设备中都很重要,因为我们可以使用它们设计更高阶的滤波器,具有非常陡峭的滚降和级联一阶和二阶滤波器,具有 n th 订单值的模拟滤波器,o dd甚至可以在合理范围内构造到任何值。
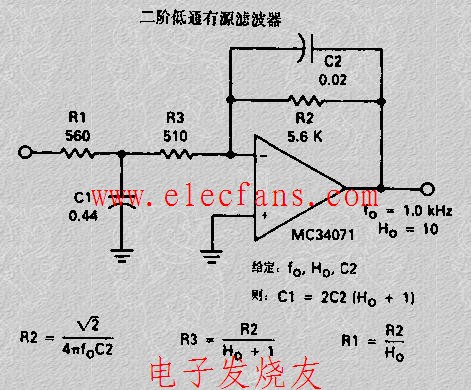
二阶低通滤波器
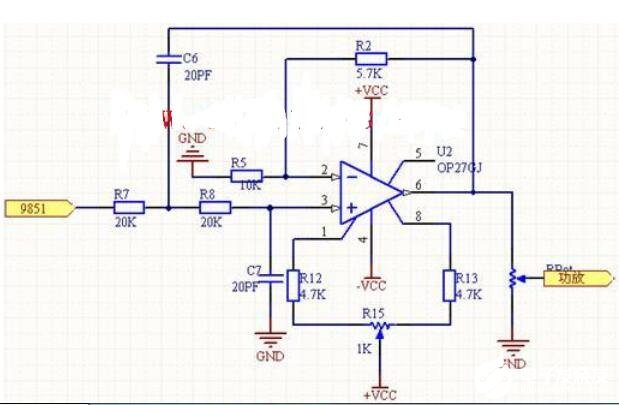
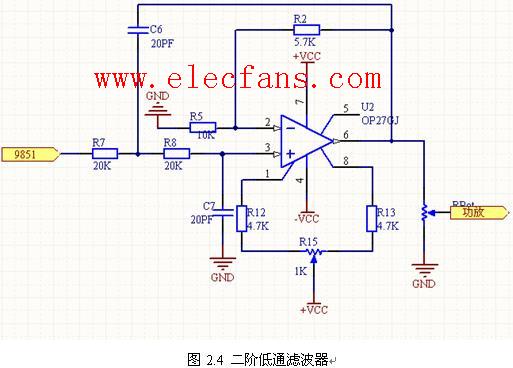
二阶低通滤波器易于设计,并广泛用于许多应用中。 Sallen-Key二阶(两极)低通滤波器的基本配置如下:
二阶低通滤波器
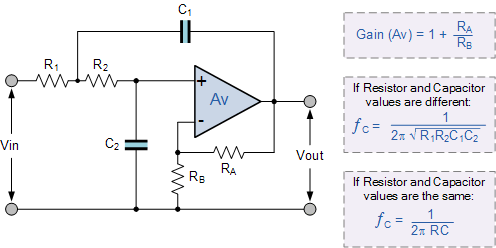
这个二阶低通滤波器电路有两个RC网络, R1 - C1 和 R2 - C2 ,它们给出滤波器它的频率响应属性。滤波器设计基于非反相运算放大器配置,因此滤波器增益 A 将始终大于1.此外,运算放大器具有高输入阻抗,这意味着它可以是容易与其他有源滤波器电路级联,以提供更复杂的滤波器设计。
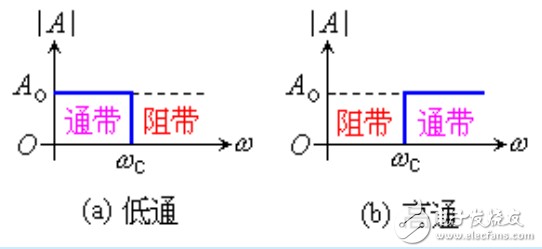
二阶低通滤波器的归一化频率响应由 RC 网络确定,通常与第一顺序类型。 1阶和2阶低通滤波器的主要区别在于,当工作频率超过截止频率时,阻带衰减将是40dB / decade(12dB /倍频程)的1阶滤波器的两倍。 ƒc,如图所示。
归一化低通频率响应
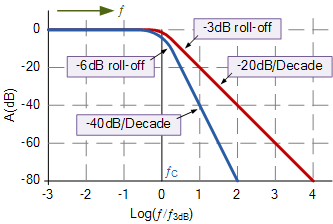
上面的频率响应波特图,基本相同对于一阶滤波器。这次的差异是滚降的陡度,在阻带中为-40dB / decade。但是,二阶滤波器可以根据截止频率点处的电路电压放大系数 Q 显示各种响应。
在有源二阶滤波器中,通常使用阻尼因子,ζ(zeta),它是 Q 的倒数。 Q 和ζ均由放大器的增益独立决定, A ,以便 Q 降低阻尼系数增加。简单来说,低通滤波器本质上总是低通,但在截止频率附近会出现谐振峰值,即由于放大器增益的共振效应,增益会迅速增加。
然后 Q ,品质因数,代表该共振峰的“峰值”,即它在截止频率点附近的高度和窄度,ƒ ç 。但滤波器增益也决定了其反馈量,因此对滤波器的频率响应有显着影响。
一般来说,为保持稳定性,有源滤波器增益不得超过3且最佳表示为:
品质因数,“Q”
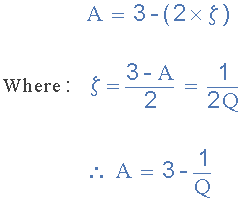
然后我们可以看到对于非反相放大器配置,滤波器增益 A 必须介于1和3之间(阻尼因子,ζ介于0和2之间)。因此,较高的 Q 值或较低的ζ值会为响应提供更大的峰值,并显示更快的初始滚降率。
二阶滤波器幅度响应
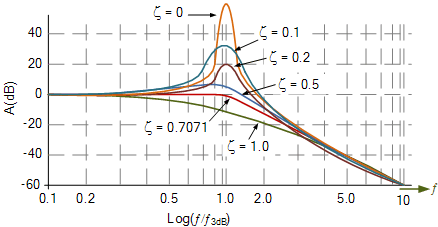
二阶低通滤波器的幅度响应因不同的值而异阻尼系数,ζ。当ζ= 1.0 或更多(2是最大值)时,滤波器变为所谓的“过阻尼”,频率响应显示长的平坦曲线。当ζ= 0 时,滤波器输出峰值在截止点处急剧上升,类似于滤波器被称为“欠阻尼”的尖点。
然后介于两者之间,ζ= 0 且ζ= 2.0 ,必须有一个频率响应具有正确值的点,并且存在。这是当滤波器“临界阻尼”并且在ζ= 0.7071 时发生。
最后一点,当反馈量达到4或更多时,滤波器开始振荡由于谐振效应,它自身处于截止频率点,将滤波器改变为振荡器。这种效应称为自振荡。然后对于低通二阶滤波器, Q 和ζ都起着关键作用。
我们可以从上面的归一化频率响应曲线中看到一阶滤波器(红线),通带增益保持平坦和水平(称为最大平坦),直到频率响应到达截止频率点时:ƒ=ƒr和增益滤波器在其最大值的 1 /√ 2 或 0.7071 时减少超过其转角频率。此点通常称为滤波器 -3dB point ,对于一阶低通滤波器,阻尼因子将等于1,(ζ= 1 )。
然而,对于二阶滤波器,这个-3dB的截止点将处于不同的频率位置,因为更陡峭的-40dB /十倍滚降率(蓝线)。换句话说,转角频率ƒr随着滤波器的阶数的增加而改变位置。然后,为了使二阶滤波器-3dB点回到与第一阶滤波器相同的位置,我们需要向滤波器添加少量增益。
因此对于Butterworth二阶低通滤波器设计增益量为:1.586,对于贝塞尔二阶滤波器设计:1.268,对于切比雪夫低通设计:1.234。
二阶滤波器示例No1
A二阶低通滤波器应设计在具有相同电阻和电容的同相运算放大器周围截止频率确定电路中的值。如果滤波器特性给出如下:Q = 5,并且ƒc= 159Hz,设计合适的低通滤波器并绘制其频率响应。
给出的特性: R1 = R2 , C1 = C2 , Q = 5 且ƒc= 159Hz
从上面的电路我们知道,对于相等的电阻和电容,截止频率点ƒc给出如下:
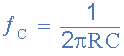
为电阻选择合适的值,例如10kΩ,得到的电容值计算如下:
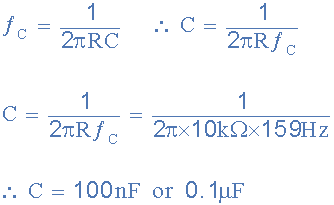
然后对于159Hz的截止转角频率, R =10kΩ和 C = 0.1uF 。
值Q = 5,滤波器增益, A 计算如下:
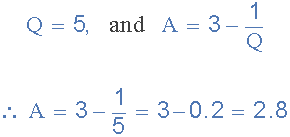
我们从上面知道,非反相运算放大器的增益如下:
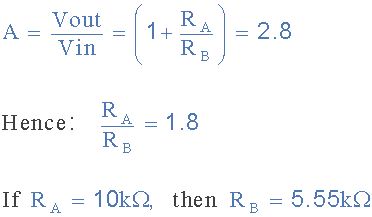
因此,二阶低通滤波器的最终电路如下:
第二订购低通滤波器电路
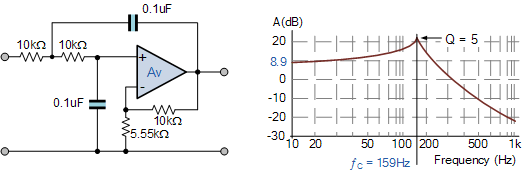
我们可以看到频率响应曲线的峰值在由于高品质因数值, Q = 5 ,截止频率。此时,滤波器的增益如下: Q×A = 14 ,或约+ 23dB,与计算值2.8相差很大,(+8.9) dB)。
但许多书籍,如右图所示,告诉我们在归一化截止频率点等处的滤波器增益应该在-3dB点。通过将 Q 的值显着降低到0.7071的值,得到的增益为 A = 1.586 ,并且频率响应为在通带中最大平坦,在截止点处具有-3dB的衰减,与二阶巴特沃斯滤波器响应相同。
到目前为止,我们已经看到二阶滤波器可以将它们的截止频率点设置为任何所需的值,但可以通过阻尼因子ζ远离此期望值。 。有源滤波器设计通过将滤波器部分级联在一起,使滤波器的阶数在合理范围内达到任何值。
实际上在设计n th 阶低通滤波器时希望设置一阶部分的截止频率(如果滤波器的阶数是奇数),并设置每个二阶部分的阻尼因子和相应的增益,以便获得正确的整体响应。为了使低通滤波器的设计更容易实现,我们可以以列表形式提供ζ, Q 和 A 的值作为有源滤波器将在Butterworth Filter教程中看到。让我们看另一个例子。
二阶滤波器示例No2
设计一个非反相二阶滤波器,它具有以下滤波器特性: Q = 1 ,ƒc= 79.5Hz 。
从上面看,过滤器的转角频率ƒc为:
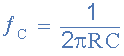
为滤波电阻选择合适的1kΩ值,然后计算得到的电容值as:
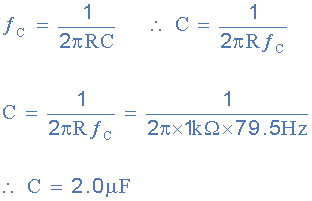
因此,对于79.5Hz或500的转角频率rads / s, R =1kΩ且 C = 2.0uF 。
给定值Q = 1,滤波器增益 A 的计算方法如下:
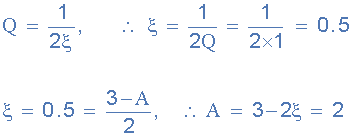
电压增益以前给出了非反相运算放大器电路:
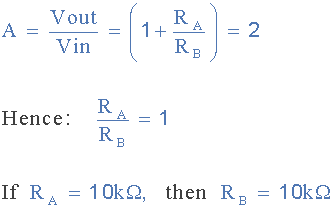
因此二阶低通滤波器电路哪个Q为1,转角频率为79.5Hz,为:
低通Fi滤波器电路
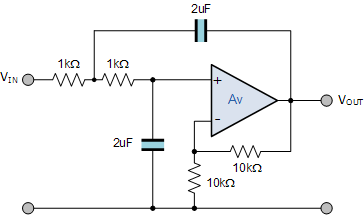
二阶高通滤波器
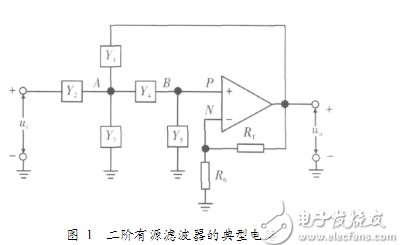
二阶低通滤波器配置和二阶高通滤波器配置,唯一改变的是电阻器和电容器的位置,如图所示。
二阶高通滤波器
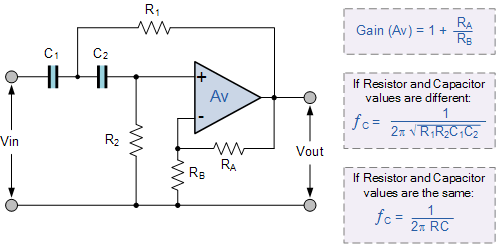
由于二阶高通和低通滤波器是相同的电路,除了电阻器和电容器的位置互换,设计和频率调整程序为高通过滤波器与前一个低通滤波器完全相同。那么二阶高通滤波器的波特图如下:
归一化高通频率响应
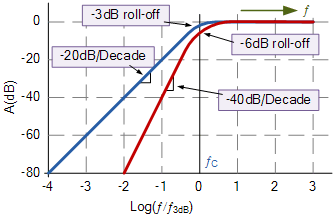
与之前的低通滤波器一样,阻带中滚降的陡度为-40dB / decade。
在上述两个电路中,op的值-amp电压增益( Av )由放大器反馈网络设置。这仅将滤波器通带内的频率增益设置得很好。我们可以选择放大输出并将此增益值设置为适合我们目的的任何量,并将此增益定义为常量 K 。
二阶Sallen-Key滤波器也称为正反馈滤波器,因为输出反馈到运算放大器的正端子。这种类型的有源滤波器设计很受欢迎,因为它只需要一个运算放大器,因此相对便宜。
-
电路
+关注
关注
173文章
5984浏览量
173251 -
滤波器
+关注
关注
161文章
7901浏览量
179282 -
频率
+关注
关注
4文章
1537浏览量
59481 -
计算
+关注
关注
2文章
452浏览量
38907
发布评论请先 登录
相关推荐
增益为1的二阶有源低通滤波器,典型二阶有源低通滤波电路
二阶压控电压源低通滤波器设计
二阶低通滤波器电路原理图_二阶低通滤波器电路结构解析
二阶有源滤波器设计





 二阶滤波器配置频率和响应案例及计算增益电路
二阶滤波器配置频率和响应案例及计算增益电路











评论